LeetCode 二叉树中第二小的节点

给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话，那么该节点的值等于两个子节点中较小的一个。
更正式地说，root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树，你需要输出所有节点中的第二小的值。如果第二小的值不存在的话，输出 -1 。

示例 1：

输入：root = [2,2,5,null,null,5,7]
输出：5
解释：最小的值是 2 ，第二小的值是 5 。

示例 2：

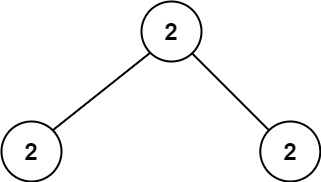
输入：root = [2,2,2]
输出：-1
解释：最小的值是 2, 但是不存在第二小的值。

提示：
树中节点数目在范围 [1, 25] 内
1 <= Node.val <= 231 - 1
对于树中每个节点 root.val == min(root.left.val, root.right.val)

方法一（深度优先搜索递归实现，层级过深会导致栈溢出问题）、
从 root 为根的树进行搜索，找到值比 cur 大的最小数。然后使用全局变量 ans 存储答案

class Solution {
    int result;
    int minVal;

    public int findSecondMinimumValue(TreeNode root) {
        result = -1;
        minVal = root.val;
        dfsRecursion(root);
        return result;
    }


    /**
     * 深度优先搜索（递归实现），层级过深会导致栈溢出问题
     * @param root root
     */
    private static void dfsRecursion(TreeNode root) {
        if(root == null){
            return;
        }

        //如果当前的第二小值不为-1时，并且当前节点值大于第二小值时说明该节点不是第二小值
        // 也说明当前节点以及该节点下的所有节点都不是所需要的结果
        if(result != -1 && root.val > result){
            return;
        }

        //如果当前节点的值大于最小值，则第二小值暂时为当前节点的val值
        if(root.val > minVal){
            result = root.val;
        }
        //递归当前节点的左节点
        dfsRecursion(root.left);

        //递归当前节点的右节点
        dfsRecursion(root.right);
    }
}

方法二（深度优先搜索非递归实现）
使用栈来将要遍历的节点压栈，然后出栈后检查此节点是否还有未遍历的节点，有的话压栈，没有的话不断出栈

class Solution {
    int result;
    int minVal;

    public int findSecondMinimumValue(TreeNode root) {
        result = -1;
        minVal = root.val;
        dfsNotRecursion(root);
        return result;
    }


    /**
     * 深度优先搜索（非递归实现）
     * @param root root
     */
    private static void dfsNotRecursion(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        //压入栈顶元素
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode treeNode = stack.pop();

            //如果当前的第二小值不为-1，并且大于result值，说明当前节点比第二小值大，
            //也该节点下的所有节点都会比result大，不需要遍历该节点下的节点，继续循环下一个节点
            if(result != -1 && treeNode.val > result){
                continue;
            }

            //如果当前节点的值大于最小值，第二小值暂时为该节点的值
            if( treeNode.val > minVal ){
                result = treeNode.val;
            }

            //栈为先入后出原则，为了保证先遍历左节点，所以先压入右节点，后压入左节点
            //先压右节点，不为空就压栈
            if(treeNode.right != null){
                stack.push(treeNode.right);
            }

            //后压左节点，不为空就压栈
            if(treeNode.left != null){
                stack.push(treeNode.left);
            }
        }
    }
}

方法三（广度优先搜索）
通过队列的方式实现，遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点

/**
 * 广度优先搜索
 * @param root root
 */
private static void bfsNotRecursion(TreeNode root) {
    if(root == null){
        return;
    }
    ArrayDeque<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);

    while(!queue.isEmpty()){
        TreeNode treeNode = queue.poll();
        //当前result为-1并且当前节点大于最小值，result暂时为该节点的值
        if(result == -1 && treeNode.val > minVal){
            result = treeNode.val;
        }
        //如果当前节点的值大于最小值并且小于当前result，result暂时为该节点的值
        if( treeNode.val > minVal && treeNode.val < result){
            result = treeNode.val;
        }
        //将该节点的左节点进入队列
        if(treeNode.left != null){
            queue.add(treeNode.left);
        }
        //将该节点的右节点进入队列
        if(treeNode.right != null){
            queue.add(treeNode.right);
        }
    }
}

转发于：https://www.ycblog.top/article?articleId=150&commentPageNum=1