数据结构笔记

最新推荐文章于 2024-12-05 11:54:25 发布

原创最新推荐文章于 2024-12-05 11:54:25 发布 · 192 阅读

0 ·

CC 4.0 BY-SA版权

数据结构与算法专栏收录该内容

2 篇文章

订阅专栏

程序效率与组织方式有关（图书馆摆书二分查找）
程序效率与操作有关（循环和递归（递归虽简单不过耗费大量空间））
程序效率与算法有关（多项式求和秦九韶要比普通算法快一个数量级）
测试两种算法的代码

#include<stdio.h>
#include<time.h>
#include<math.h> 
#define MAX 101
#define MAXL 1e7
clock_t start,stop;
double duration;
double f1(int n,double a[],double x)
{
	int i;
	double p=a[0];
	for(i=1;i<=n;i++)
	{
		p+=(a[i]*pow(x,i));
	}	
	return p;
}
double f2(int n,double a[],double x)
{
	int i;
	double p=a[n];
	for(i=n;i>0;i--)
	{
		p=a[i-1]+x*p;
	}	
	return p;
}
int main()
{
	double a[MAX];
	int i;
	for(i=1;i<=MAX-1;i++){
		a[i]=(double)i;
	}
	start = clock();
	for(i=0;i<=MAXL;i++){
		f1(MAX-1,a,1.1);
	}
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/MAXL;	
	printf("%6.2e\n",duration);
	
	start = clock();
	for(i=0;i<=MAXL;i++){
		f2(MAX-1,a,1.1);
	}
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/MAXL;	
	printf("%6.2e\n",duration);
	return 0;	
}

线性结构（一对一）
树形结构（一对多）
图形结构（多对多）

空间复杂度（内存开辟了多少空间）
时间复杂度（计算了多少次乘除法）
一般考虑复杂度只考虑最坏的复杂度而不去考虑平均复杂度
复杂度的渐进表示法
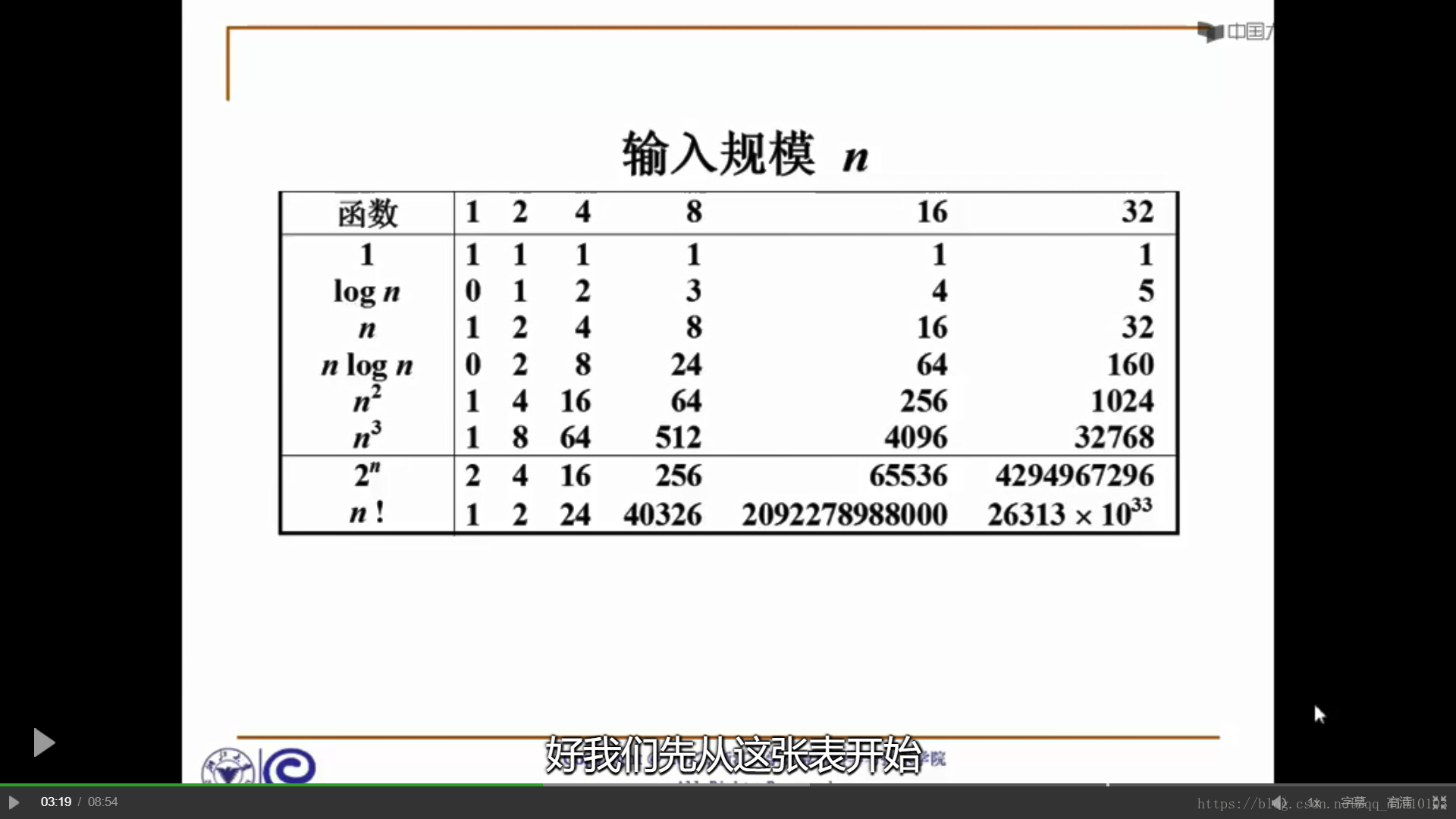
在这里插入图片描述

在这里插入图片描述
nlogn

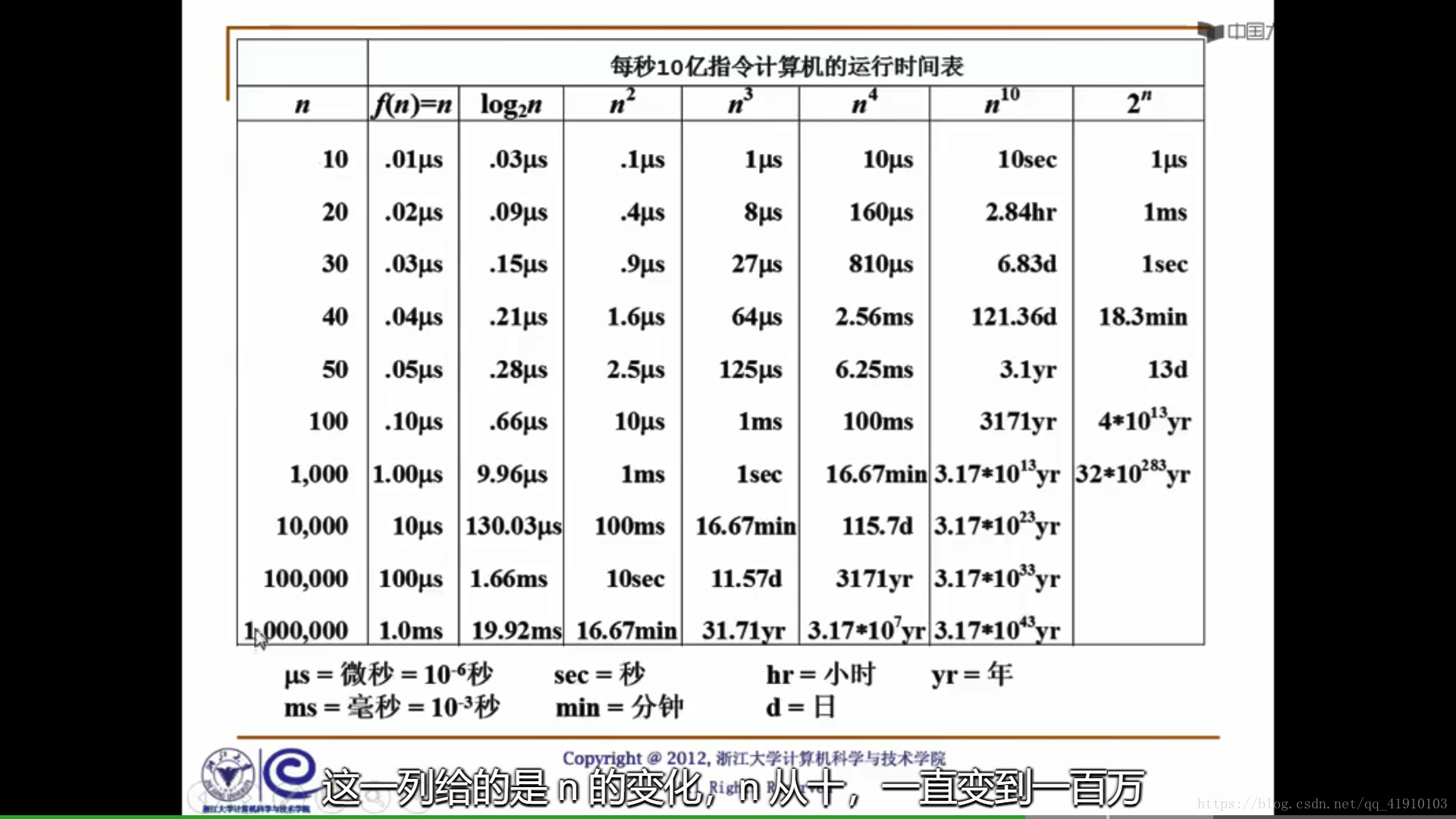
在这里插入图片描述
求时间复杂度

最大子序列

本题算法的时间复杂度
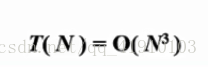
在这里插入图片描述

在这里插入图片描述
分而治之的思想很好

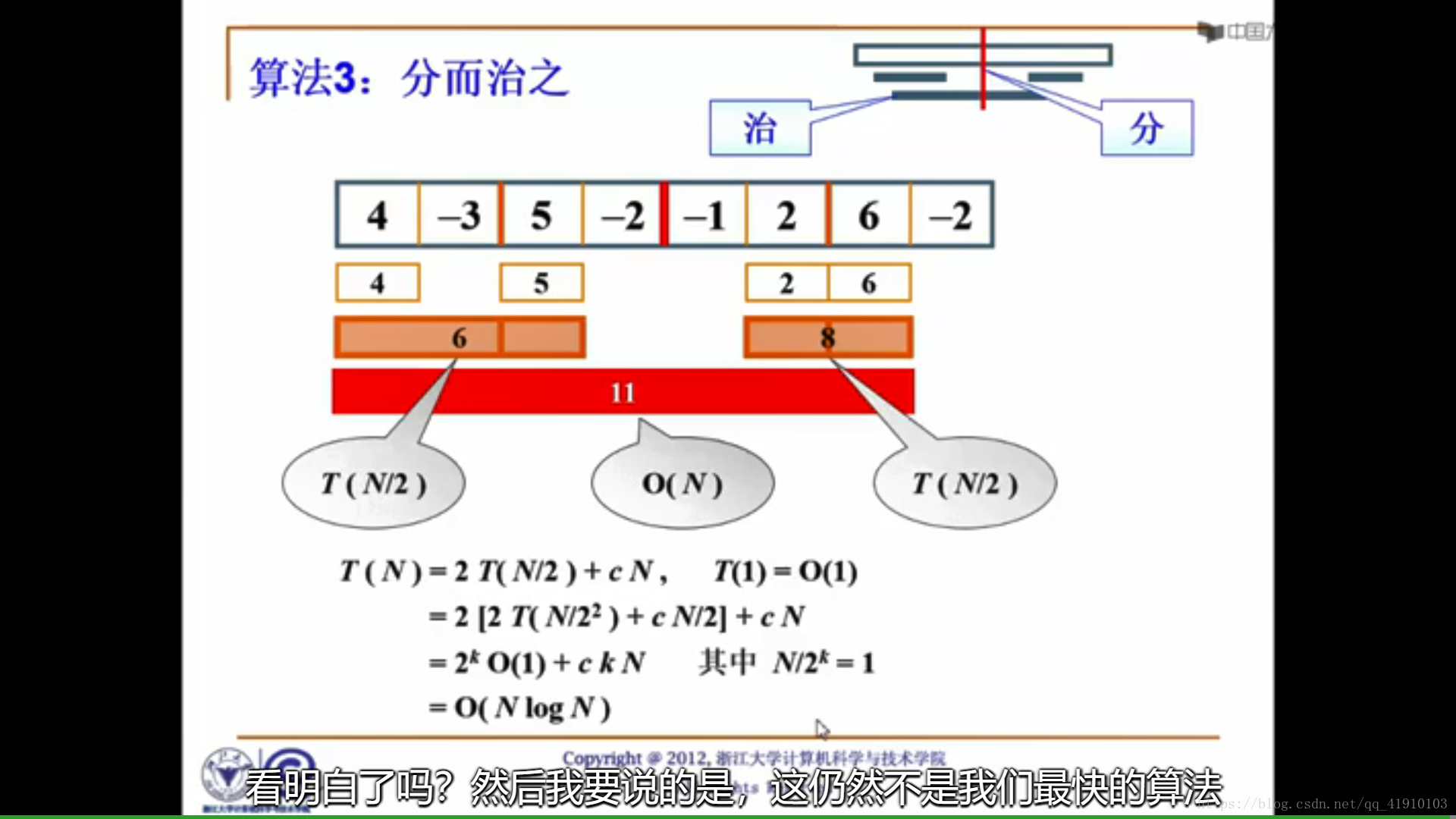
在线即使处理

最大子列和最快算法

#include <stdio.h>
int Fun(int a[],int n);
int main()
{    
    int n,i;
    scanf("%d", &n);
    int a[n];
    for(i=0;i<n;i++)
    {
    	scanf("%d",&a[i]);
    }
    printf("%d\n", Fun(a,n));
    return 0;
}
int Fun(int a[],int n)
{
	int thisSum,Maxsum,i;
	thisSum=Maxsum=0;
	for(i=0;i<n;i++)
	{
		thisSum+=a[i];
		if(thisSum>Maxsum){
			Maxsum=thisSum;
		}
		if(thisSum<0){
			thisSum=0;
		}
	}	
	return Maxsum;
}

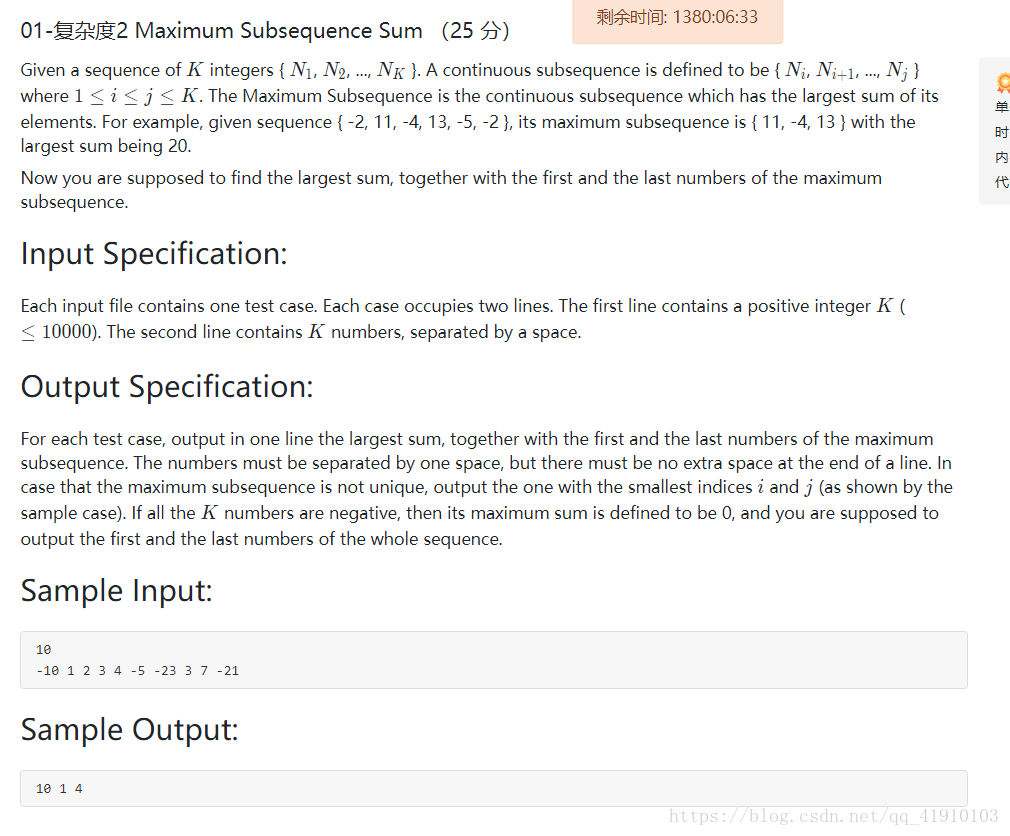
在这里插入图片描述
最大子列和升级版要求出最大子列和的首尾

#include <iostream>
#include <vector>
using namespace std;
int MaxSubseqSum(vector<int> numbers, int num);
int mybegin, myend, newbegin;
int main()
{   int num = 0;
    cin >> num;
    vector<int> numbers(num);
    for (int i = 0; i<num; i++)
        cin >> numbers[i];
    int MaxSum = MaxSubseqSum(numbers, num);
    cout << MaxSum << " " << numbers[mybegin] << " " << numbers[myend] << endl;
    system("pause");
    return 0;
}
int MaxSubseqSum(vector<int> numbers, int num)
{
    int ThisSum = 0, MaxSum = -1;
    int i;
    bool newMyBegin = true;
    for (i = 0; i < num; ++i) {
        ThisSum += numbers[i];
        if (ThisSum > MaxSum) {
            MaxSum = ThisSum;
            myend = i;
            if (newMyBegin) {
                mybegin = newbegin;
                newMyBegin = false;
            }
        }
        else if (ThisSum < 0) {
            ThisSum = 0;
            newMyBegin = true;
            newbegin = i + 1;
        }
    }
    if (MaxSum == -1) {
        mybegin = 0;
        myend = num - 1;
        return 0;
    }
    return MaxSum;
}