浅谈数据结构之：二叉树与二叉树的增删改查

本文纯自己的一些独到感受和理解，长期努力完善和总结~

————————————分割线————————————

一、数据结构是什么？

     数据结构是指互相之间存在着一种或多种关系的数据元素的集合。且数据结构和数据元素之间存在逻辑关系，数据在计算机上的存储方式和在数据上定义的运算，可以归纳为三个方面：数据的逻辑结构、数据的存储结构和数据的运算。

二、二叉树是什么？

    二叉树是有限个数据元素的集合，该集合或者为空、或者由一个称为根节点所携带的元素及两个不相交的，被分别成为左子树和右子树组成。当集合为空时，称二叉树为空二叉树。然而二叉树组成左右子树是有一定要求的。比如：

 

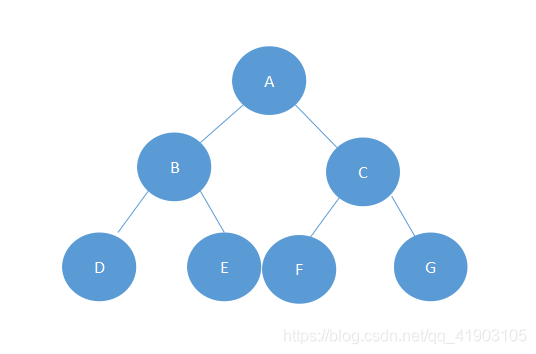
由图可以看出，该二叉树叶子结点在同一层且是满的，所以该图是一个满二叉树。

而又可以知道该集合数的大小关系：G>C>F>A>E>B>D。这里可以总结，如果结点（子节点）所拥有的值小于对于它的父节点的值，那么应该是它父节点的左子树，相反就是它的右子树。拿ABC三个值来说，因为B<A，所以B应该是A的左子树，相反C>A，C应该是A的右子树，那么定义根节点的要求又是什么呢？这个得看你数组或者集合中的值的第一个了，若没有进行别的处理的时候把第一个值当作根结点会方便很多~当然数值太小不便于建树噢！

————————————————————————————

下面附JAVA建二叉树的代码：

    public static void insertTree(TreeNode tr, Integer value) {    
        if(tr.getValue()==null)
        {
                  tr.setValue(value);
                  }//如果第一个结点没有值，将第一个数据放入该节点
        else{
            if( value<=tr.getValue())
            {
                if( tr.getLeftNode()==null )
                {
                    tr.setLeftNode(new TreeNode());//如果左子树没有值，放入值
                }
                    tr=tr.getLeftNode();//否则放入左子树
                    insertTree(tr,value);//回调函数在进行判断
            }
            else{
                if( tr.getRightNode()==null )
                {
                    tr.setRightNode(new TreeNode());
                }
                    tr=tr.getRightNode();
                    insertTree(tr,value);
            }
        }
    }//插入算法

		public static void search(Treenode tr,int data){
			if(tr.getValue().intValue()==data){
				System.out.println("找到了"+data);
				
			}
			else{
				if(data < tr.getValue().intValue()){//判断左边
					if(tr.getLeftNode()== null){//输出找不到
						System.out.println("该树没有");
					}
				else
				   {
					search(tr.getLeftNode(),data);
				   }
		}
			else if(data > tr.getValue().intValue()){
				if(tr.getRightNode()== null)
				    {//输出找不到
					System.out.println("该树没有");	
					}
				else
				   {
					search(tr.getRightNode(),data);
				   }
				}
			}
		}//查找二叉树



		public static Treenode searchRightmin(Treenode tr){//找删除树的左边最大的
			if(tr.getRightNode() == null){
				return tr;
			}
			else{
				return searchRightmin(tr.getRightNode());
			}

		}
		
		public static Treenode searchLeftmax(Treenode tr){//删除数右边最小的
			if(tr.getLeftNode()== null){
				return tr;
			}
			else{
				return searchLeftmax(tr.getLeftNode());
			}

		}