采样与量化
成像传感器
成像传感器就像是眼睛视网膜上的视觉神经细胞,它会将收到的能量转换成相应比例的电信号,传感器有单个成像传感器、条带传感器、阵列传感器
| 类别 | 形状 | 成像方式 |
|---|---|---|
| 单个成像传感器 |  | 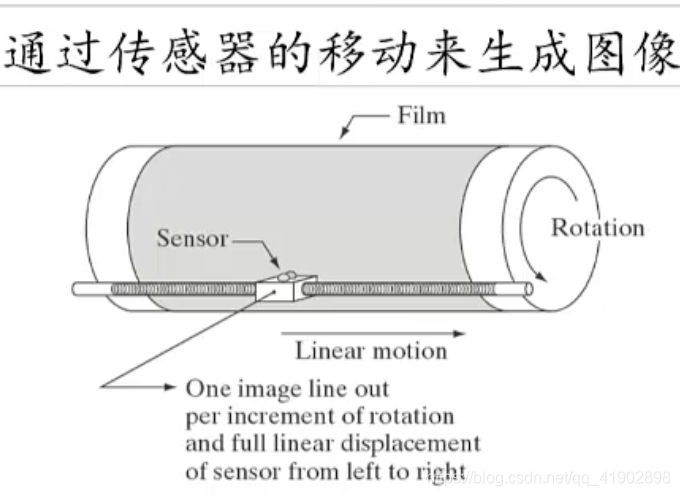 |
| 条带传感器 |  | 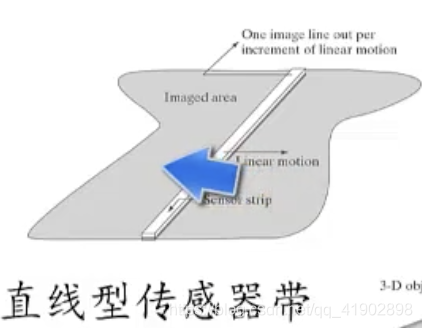 |
| 阵列传感器 |  |  |
采样与量化
通过传感器获得模拟信号后,需要对模拟信号数字化才能得到我们的数字图像。采样就是将连续的空间进行离散化处理,量化就是将连续型的信号幅值离散化处理。
| 首先将空间离散化,每个二维平面都可以看作是无数条线段组成的,从中取出一条线段AB |  |
|---|---|
| AB之间的信号幅值实际是连续的 |  |
| 将幅值划分为有限个区间,每个区间用一个数字来表示,那么采样的AB间信号幅值可以用划分的区间来表示,就完成了对连续的模拟信号数字化 |  |
| 由于采样与量化都是将原本连续的数据离散化,这个过程必然会带来数据的损失 |  |
数字图像的表示
| 数字图像通常可以用一个二维离散函数 f ( x , y ) f(x, y) f(x,y)来表示,其中 ( x , y ) (x, y) (x,y)代表空间坐标,每个像素点的 f ( x , y ) f(x, y) f(x,y)就代表该点的信号值。 |  |
|---|---|
| 第二种方式就是直接使用显示器显示数字图像 |  |
| 第三种方式是使用二维矩阵或者数组来表示数字图像,这种方法在数字图像处理中最常见 |  |
所有数字图像的原点都是在左上角,图像的每个采样点被称为像素
图像的存储大小
假设一副数字图像量化时使用了L个灰度级,其中由于技术原因L只能是2的整数次幂,即 L = 2 k L=2^k L=2k。那么图像的大小 S = M ∗ N ∗ k ( b i t ) S=M * N * k (bit) S=M∗N∗k(bit),这种图像称为k比特图,通常我们使用的图像都是一个像素点有8bit大小。
空间分辨率
空间分辨率是对图像中可辨别最小细节的度量,它的单位可以是dpi(dot per inch)即每英寸的点数来表示,一副图像包含的像素个数也可以代表空间分辨率。

强度分辨率
强度分辨率是指强度级别上可以识别的最小变化,用于量化强度的位数可以表示“强度分辨率”。如k比特图,它的强度分辨率就是k。观察下面图可以发现在随着图像强度下降,图像出现了伪轮廓、假边界以及细节模糊,最后一张图已经丢失了图像大部分内容。

像素间关系
图像插值
当在查看数字图像时,想要将图像放大,放大意味着局部图像会由小变大,需要用来表示的像素点会变多,那么这些多出像素点就是利用图像插值技术,用已知数据估计未知位置的值。图像插值主要有三种方式:
最近邻插值使用最近邻的强度作为未知位置的值
双线性插值使用4个最近邻来估计给定位置的强度
双三次插值使用16个最近邻来估计给定位置的强度
比较上面三种算法可发现,每种算法使用到的邻域信息不同,使用的邻域信息越多的算法越强大,但是同时也会带来算法复杂度的增加。
像素的邻域
上面三个方法都提到了“近邻”概念,在图像处理中像素点之间的距离计算有多种方法,不同算法使用的最近邻计算可能不同。
| 4-邻域:坐标 ( x , y ) (x,y) (x,y)处的像素点p的两个水平和两个垂直的相邻点 N 4 ( p ) : ( x + 1 , y ) , ( x − 1 , y ) , ( x , y + 1 ) , ( x , y − 1 ) N_4(p): (x+1,y),(x-1,y),(x,y+1),(x,y-1) N4(p):(x+1,y),(x−1,y),(x,y+1),(x,y−1) |  |
|---|---|
| D-邻域:坐标(xy)处的像素点p的四个对角线相邻点 N D ( p ) : ( x + 1 , y + 1 ) , ( x + 1 , y − 1 ) , ( x − 1 , y + 1 ) , ( x − 1 , y − 1 ) N_D(p): (x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1) ND(p):(x+1,y+1),(x+1,y−1),(x−1,y+1),(x−1,y−1) |  |
| 8-邻域:坐标 ( x , y ) (x,y) (x,y)处的像素点p的4邻域和D邻域的和 N 8 ( p ) = N 4 ( p ) + N D ( p ) N_8(p)=N_4(p)+N_D(p) N8(p)=N4(p)+ND(p) |  |
像素的邻接关系
| 4邻接: 如果两个像素点p和q具有相似的值,或者说它们的值来自于同一集合V ,并且q位于p的4-邻域中。 | 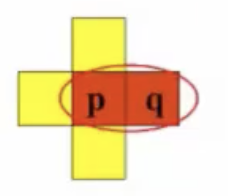 |
|---|---|
| 8-邻接:如果两个像素点p和q具有相似的值,或者说它们的值来自同一集合V;并且q位于p的8-邻域中。 |  |
| m-邻接(混合邻接):如果两个像素点p和q具有相似的值,或者说它们的值来自于同一集合V;并且q位于p的4-邻域中;或者q位于p的D-邻域中并且 N 4 ( p ) ∩ N 4 ( p ) N_4(p)\cap{N_4(p)} N4(p)∩N4(p)中没有像素的值来自于V; | 显然左边图符合m-邻接,而右边违反了
N
4
(
p
)
∩
N
4
(
p
)
N_4(p)\cap{N_4(p)}
N4(p)∩N4(p)的规则 |
在定义了像素点之间的邻接关系后,我们肯定会有疑问,这样做的目的是什么?下面给出一个简单案例来解释。
可以看到在上图中,根据定义的规则,4-邻接能够连接的像素点只有三个,但是右下角那个像素显然是和这三个像素点有联系,但是4-邻接却将他们割裂开来了。
再看第二张图,根据8-邻接规则,右上角的三个像素点之间都是8-邻接关系,像素点之间关系不明确,存在多条通路,就会造成模糊不清的情况。
第三张图是m-邻接,根据m-邻接的规则,像素点间有且仅有一条通路,不会造成模糊也不会丢失信息。
通路
从坐标为(x,y)的像素点p到坐标为(x,yn)的像素点q间的通路用像素点序列来表示
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
…
,
(
x
n
,
y
n
)
(x_0,y_0),(x_1,y_1),…,(x_n,y_n)
(x0,y0),(x1,y1),…,(xn,yn)
其中坐标为
(
x
i
−
1
,
y
i
−
1
)
(x_{i-1},y_{i-1})
(xi−1,yi−1)的像素点与坐标为
(
x
,
y
)
(x,y)
(x,y)的像素点具有邻接关系,
1
≤
i
≤
n
1≤i≤n
1≤i≤n
基于不同邻接关系得到的通路不同,例如,基于4-邻接关系得到的通路是4-通路,依次类推。
像素点间距离度量
假设像素点和q的坐标分别为:
(
x
,
y
)
,
(
u
,
v
)
(x,y),(u,v)
(x,y),(u,v)
欧氏距离:
D
e
(
p
,
q
)
=
[
(
x
−
u
)
2
+
(
y
−
v
)
2
]
1
2
D_e(p,q)={[(x-u)^2+(y-v)^2]}^\frac{1}{2}
De(p,q)=[(x−u)2+(y−v)2]21
街区距离:
D
4
(
p
,
q
)
=
∣
x
−
u
∣
+
∣
y
−
v
∣
D_4(p,q)=|x-u|+|y-v|
D4(p,q)=∣x−u∣+∣y−v∣
棋盘距离:
D
8
(
p
,
q
)
=
m
a
x
(
∣
x
−
u
∣
,
∣
y
−
v
∣
)
D_8(p,q)=max(|x-u|,|y-v|)
D8(p,q)=max(∣x−u∣,∣y−v∣)
以上三种距离都只是考虑的像素点间的空间距离,而没有考虑像素点的强度,前面讲到邻接关系就是用来描述像素点之间的相似关系的,而通路则是同一种邻接关系像素点的集合
D
m
D_m
Dm距离:两个像素点间的最短m通路的长度,其中通路长度是指这条通路上面像素点存在的个数
图像算术操作

图像的基本四则运算就是用相同位置的像素点的强度值进行计算,但是如果只是简单的四则运算会带来一些问题,如,计算后的强度值超过规定范围,或者是强度值小于0。对于超过规定范围的值会取最大强度值,小于0的取0.但是这样以来肯定会使图像的部分信息丢失。
好在可以通过对图像进行尺度规范化或尺度缩放,可以使图像尽可能的保存全部的信息
1、
g
m
=
g
−
m
i
n
(
g
)
g_m=g-min(g)
gm=g−min(g)
2、
g
s
=
K
[
g
m
/
m
a
x
(
g
m
)
]
g_s=K[g_m/max(g_m)]
gs=K[gm/max(gm)]

以上面的减法为例,得到的像素点值存在负数,通过第一步计算,
m
i
n
(
g
)
=
−
7
min(g)=-7
min(g)=−7,所有点减去-7后,可以得到
g
m
=
(
0
8
4
9
)
g_m=\begin{pmatrix} 0 & 8 \\ 4 & 9 \end{pmatrix}
gm=(0489)。再通过第二步计算,
m
a
x
(
g
m
)
=
9
max(g_m)=9
max(gm)=9,所有点除去9后,可得
(
0
8
9
4
9
1
)
\begin{pmatrix} 0 & \frac{8}{9} \\ \frac{4}{9} & 1 \end{pmatrix}
(094981),再乘想要设定的灰度值范围K,这里假设K=255,也就是0~255 。最终得到
g
s
=
(
0
227
113
255
)
g_s=\begin{pmatrix} 0 & 227\\ 113& 255 \end{pmatrix}
gs=(0113227255) 。
通过上述的变换,得到的像素点值只会是规定强度值内的值。
加法去除随机噪声

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








