一、贪心的思路
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
步骤:
将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解
455.分发饼干
题目
思路:
思路1:用大饼干优先给大胃口的;
思路2:小饼干先满足小胃口的;
时间复杂度:
sort函数为O(nlogn+mlogm), for循环是g和s中较小的O(min(m,n))
因此总的为O(nlogn+mlogm)。
注意点:
for循环要看控制的是饼干还是人。
反思:
- 我用了sort函数将数组进行从大到小排列;随想录是直接倒着遍历的,效率更高。
- sort函数:《C++primer345》
我的:
class Solution {
public:
static bool cmp(int a,int b)
{
return a>b;
}
int findContentChildren(vector<int>& g, vector<int>& s) {
int sum=0;
sort(g.begin(),g.end(),cmp);
sort(s.begin(),s.end(),cmp);
for(int i=0,j=0;i<g.size()&&j<s.size();i++)
{
if(s[j]>=g[i])
{
sum++;
j++;
}
}
return sum;
}
};
随想录:
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
int sum=0;
sort(g.begin(),g.end());
sort(s.begin(),s.end());
for(int i=g.size()-1,j=s.size()-1;i>=0&&j>=0;i--)
{
if(s[j]>=g[i])
{
sum++;
j--;
}
}
return sum;
}
};
376. 摆动序列
122.买卖股票的最佳时机II
题目
方法1:贪心
思路:
局部最优解:每天的利润最大化
全局最优解:只收集每天的正利润,最后累计成全局最优
破解口
就是能够想到分解,计算相邻两天的利润。即将一个区间prices[5]-prices[4]分解成(prices[2]-prices[1])+(prices[3]-prices[2])+(prices[4]-prices[3])+(prices[5]-prices[4]),就变成了相邻天数的利润相加。
贪心算法只是求得了最后的最大利润,没有真正模拟交易。
我写的:
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res=0;
for(int i=1;i<prices.size();i++)
{
int t=prices[i]-prices[i-1];
if(t>0)
res+=t;
}
return res;
}
};
随想录:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 1; i < prices.size(); i++) {
result += max(prices[i] - prices[i - 1], 0);
}
return result;
}
};
方法2: 动态规划
55. 跳跃游戏
题目
思路:
破解口: 这里的贪心体现在每次取最大跳跃步数,然后根据范围看是否能够覆盖终点坐标。 比如nums[i]=3,
而没有去纠结具体跳1,2,3个,因为总能跳到3格的位置。
注意:
for循环中必须是<=cover,否则不能过[3,2,1,0,4]这个样例,因为只有步数不为0才能跳,而<=nums.size()-1, 当步数为0时依旧可以跳。
跳到下一个是用:i+nums[i]
//8:20
class Solution {
public:
bool canJump(vector<int>& nums) {
int cover=0;
if(nums.size()==1) return true;
for(int i=0;i<=cover;i++) //这里是<=cover
{
cover=max(cover,i+nums[i]);
if(cover>=nums.size()-1)
return true;
}
return false;
}
};
45. 跳跃游戏2
题目
思路:
每次记录的是覆盖范围内的跳跃最大值,作为下一次跳跃的起点。因为当到达跳跃边界点时,就需要再走一步,继续往前跳,所以for循环只需要到nums.size()-1。
破解口:
这里的贪心体现在哪?
题目要求最小的步数,但是还是要以覆盖范围来思考,因为覆盖范围是怎样都能够跳到的,而下一步跳哪呢?应该是以覆盖范围终点开始跳能够跳的最远距离即最大的扩大覆盖范围,如何找这个下一跳的最大范围?就是在上次的覆盖范围内找到nums[i]最大的那一个,那么下一跳的起点就是覆盖范围终点+max(nums[i])。
我的困惑:
想要遍历,但是又不知道怎么和贪心联系起来,根源是要从最大覆盖范围来思考贪心,以及下一跳能够跳的最大距离。
class Solution {
public:
int jump(vector<int>& nums) {
int end=0;
int maxPos=0;
int res=0;
for(int i=0;i<nums.size()-1;i++)
{
maxPos=max(maxPos,i+nums[i]);
if(i==end)
{
end=maxPos;
res++;
}
}
return res;
}
};
1005. K 次取反后最大化的数组和
题目
我的思路:
从小到大排序,先把负数的给消耗掉,然后再次排序,剩下的k看是偶数还是奇数,偶数就不用干啥,奇数就给最小的变为相反数即可。
我的问题:
- 没有用到贪心去思考问题
- 使用了两次排序,不够最优
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
int sum=0;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++)
{
if(k>0&&nums[i]<0)
{
k--;
nums[i]=-nums[i];
}
}
sort(nums.begin(),nums.end()); //得再次排序
if(k>0&&k%2!=0)
{
nums[0]=-nums[0];
}
for(int i=0;i<nums.size();i++)
sum+=nums[i];
return sum;
}
};
随想录:
优化:使用绝对值排序,就不用最后再排序一次了。
使用了两次贪心想法:
第一次贪心:有负数和正数混合,将最小的负数变成正数,成为全局和最大
第二次贪心:当全部变成正数后,将最小的正数变成负数,使全局和最大
class Solution {
static bool cmp(int a, int b) {
return abs(a) > abs(b);
}
public:
int largestSumAfterKNegations(vector<int>& A, int K) {
sort(A.begin(), A.end(), cmp); // 第一步
for (int i = 0; i < A.size(); i++) { // 第二步
if (A[i] < 0 && K > 0) {
A[i] *= -1;
K--;
}
}
if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
int result = 0;
for (int a : A) result += a; // 第四步
return result;
}
};
134. 加油站
题目
方法一:暴力法
我写的:结果运行超时
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int sum=0;
int res=0;
int n=gas.size();
int i=0;
for(int j=0;j<n;j++)
{
i=j;
sum=gas[j];
while(sum>=0)
{
sum=sum-cost[i%n];
if(sum>=0)
sum=sum+gas[(i+1)%n];
else break;
i=(i+1)%n;
if(i==j) break;
}
if(sum>=0&&i==j)
return i;
}
return -1;
}
};
随想录:
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
for (int i = 0; i < cost.size(); i++) {
int rest = gas[i] - cost[i]; // 记录剩余油量
int index = (i + 1) % cost.size();
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)
rest += gas[index] - cost[index];
index = (index + 1) % cost.size();
}
// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
if (rest >= 0 && index == i) return i;
}
return -1;
}
};
方法二:贪心
860.柠檬水找零
题目
我的思路:
刚开始想用sum来计数挣得钱,看是否能够有足够多的钱找零,但是是错误的,因为是要看”能不能找开“,而不是”能不能找“。又换成了数组记录5 10 20 的个数,但是实际上只需要记录5 10 就够了,因为20不能找任何,是最大的,也不需要用数组,只需要用两个变量即可。
并且我也没有想到贪心的思想,只是用模拟的方法解出的。因此很侥幸,因为应该先消耗10,再消耗5,所以是有顺序的。当我先消耗三个5来找零20时就出错了,如下图:
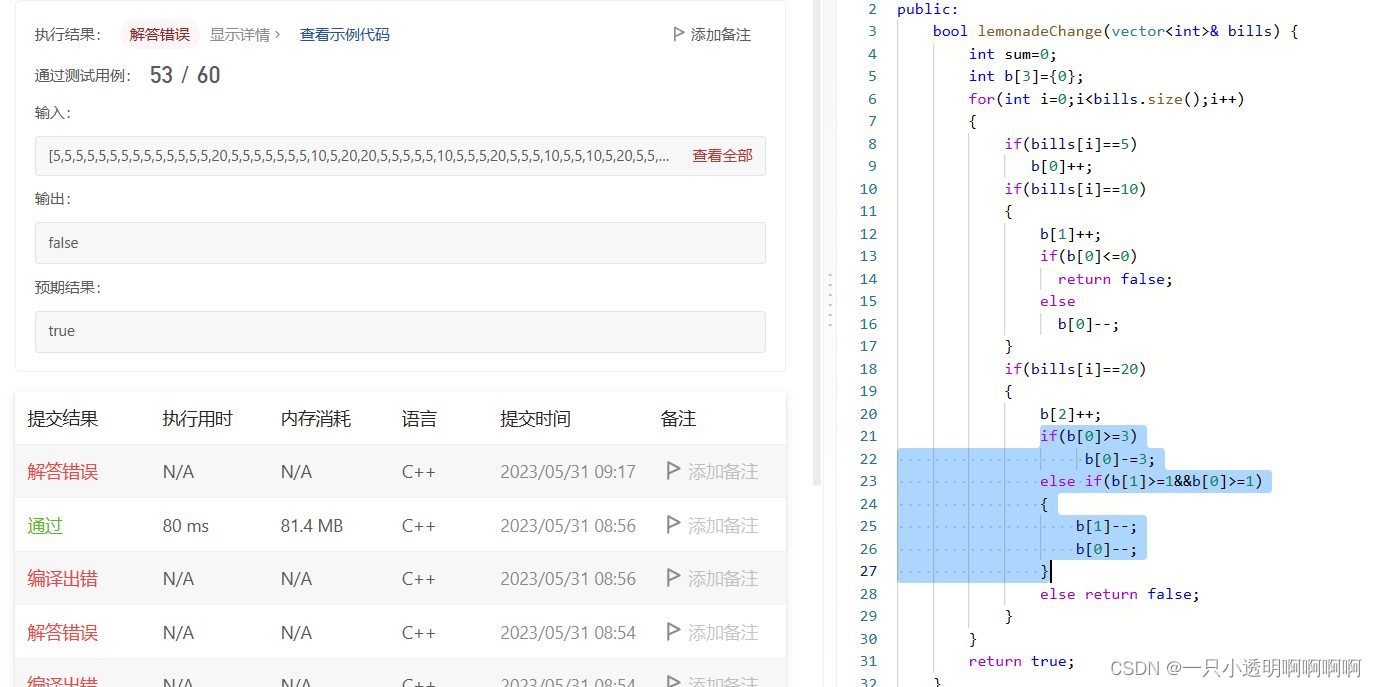
我的代码:
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int sum=0;
int b[3]={0};
for(int i=0;i<bills.size();i++)
{
if(bills[i]==5)
b[0]++;
if(bills[i]==10)
{
b[1]++;
if(b[0]<=0)
return false;
else
b[0]--;
}
if(bills[i]==20)
{
b[2]++;
if(b[1]>=1&&b[0]>=1) //先消耗10
{
b[1]--;
b[0]--;
}
else if(b[0]>=3)
b[0]-=3;
else return false;
}
}
return true;
}
};
随想录:
【贪心思路】
因为5既能找零10,也能找零20,所以更万能,因此找零20的时候,先用10+5的形式,再用5+5+5的形式。
其他情况是固定的,当是5时不需要找零,当是10时,找零5即可。
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five=0,ten=0;
for(int i=0;i<bills.size();i++)
{
if(bills[i]==5)
five++;
if(bills[i]==10)
{
if(five<=0)
return false;
ten++;
five--;
}
if(bills[i]==20)
{
if(ten>=1&&five>=1)
{
five--;
ten--;
}
else if(five>=3)
five-=3;
else return false;
}
}
return true;
}
};
406. 根据身高重建队列
452. 用最少数量的箭引爆气球
题目
我的思路:只想到了按照左边进行排序,但是不知道怎么选择引爆的位置,以及与下一个气球之间如何有联系,随想录的思路是,将区间左边从小到大排列后,引爆的位置选择重叠气球的右边最小的位置A,这样下一个气球直接看开始位置是否大于A。
























 862
862

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








