D. Relatively Prime Graph codeforces 1009 D

                                                 

D. Relatively Prime Graph

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's call an undirected graph G=(V,E)G=(V,E) relatively prime if and only if for each edge (v,u)∈E(v,u)∈E  GCD(v,u)=1GCD(v,u)=1 (the greatest common divisor of vv and uu is 11). If there is no edge between some pair of vertices vv and uu then the value of GCD(v,u)GCD(v,u) doesn't matter. The vertices are numbered from 11 to |V||V|.

Construct a relatively prime graph with nn vertices and mm edges such that it is connected and it contains neither self-loops nor multiple edges.

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

If there are multiple answers then print any of them.

Input

The only line contains two integers nn and mm (1≤n,m≤1051≤n,m≤105) — the number of vertices and the number of edges.

Output

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

Otherwise print the answer in the following format:

The first line should contain the word "Possible".

The ii-th of the next mm lines should contain the ii-th edge (vi,ui)(vi,ui) of the resulting graph (1≤vi,ui≤n,vi≠ui1≤vi,ui≤n,vi≠ui). For each pair (v,u)(v,u)there can be no more pairs (v,u)(v,u) or (u,v)(u,v). The vertices are numbered from 11 to nn.

If there are multiple answers then print any of them.

Examples

input

Copy

5 6

output

Copy

Possible
2 5
3 2
5 1
3 4
4 1
5 4

input

Copy

6 12

output

Copy

Impossible

Note

Here is the representation of the graph from the first example: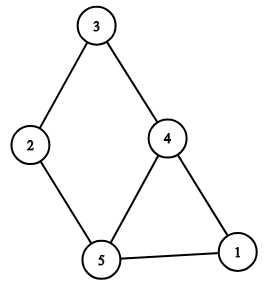

 

 

题意：给出n，m表示有n个点编号（1-n），你要构造一个m条边的的图形，使得相连的两个点互为素数，如果可以构造出，输出 Possible 并且输出所有边的关系，否则输出   Impossible

 

思路：首先，如果m<n-1的话，直接可以排除了，因为n个点最小要用n-1条边，然后，我们可以只要暴力不断以节点和与之互素的节点建边即可（gcd的复杂度非常小，所以可以直接用gcd来判断，据说，gcd递归的次数不会超过较小的那个数的5倍）

 

#include "iostream"
#include "vector"
using namespace std;
const int Max=1e5+10;
vector<int> G[Max];
int X[Max],Y[Max];
int gcd(int a,int b)
{
  return b?gcd(b,a%b):a;
}
int main()
{
  int n,m,ans=0,tot=0;
  cin>>n>>m;
  if(m<n-1){cout<<"Impossible"<<endl; return 0;}
  int x=3,t=2;  m-=n-1;//1和所有其他点gcd=1所以先减去n-1，从2开始枚举
  while(m&&t<n){
    while(gcd(t,x)!=1) x++;
    if(x>n) {t++;x=t+1;continue;}
    X[tot]=t,Y[tot++]=x;
    x++,m--;
  }
  if(m>0) cout<<"Impossible"<<endl;//枚举完所有点，边还没用完，那么一定不可以
  else{
    cout<<"Possible"<<endl;
    for(int i=1;i<n;i++) cout<<"1 "<<i+1<<endl;
    for(int i=0;i<tot;i++)
      cout<<X[i]<<" "<<Y[i]<<endl;
  }
  return 0;
}