排序算法知识点总结和Java实现

于 2020-03-19 21:32:43 发布
阅读量441 收藏 7
点赞数 2
分类专栏： 算法 文章标签： 算法 java 排序算法 快速排序 堆排序
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_41872247/article/details/104964958
版权

排序算法知识点总结和Java实现

前言

文章会有一些从参考材料中转载来的动图，如果构成侵权，请留言联系我，我会删除这些部分。
参考代码（都是正文的代码）：https://download.youkuaiyun.com/download/qq_41872247/12320616

1. 术语解释

  1. 稳定排序：假设待排序数组中有a == b，且a在b的前面，排序之后a仍然在b前面，这样的排序叫稳定排序。
  2. 不稳定排序：假设待排序数组中有 a == b，且a在b的前面，排序之后a可能会在b的后面，这样的排序叫不稳定排序。
  3. 原地排序：排序过程中不需要申请额外空间（如数组）的排序叫原地排序。
  4. 非原地排序：排序过程中需要申请额外空间（如数组）的排序叫非原地排序。
  5. 时间复杂度：排序算法所花费的时间，如果没有指明就是指平均时间复杂度。
  6. 空间复杂度：排序算法所花费的空间（也就是申请内存的大小）。
  7. 最好情况和最坏情况：排序算法在某种情况下所花费的最少（最多）的时间（不包括空间）。
  8. 比较排序：通过比较两个数的大小来进行排序的方法，绝大部分排序算法都是比较排序。
  9. 非比较排序：不通过比较而是其他的方法进行排序。

有些时候面试官问你XX算法在什么情况下效率较好，效率较差等，这种就是在问你什么时候接近最好情况和接近最坏情况了。

空间复杂度介绍：仅需要申请数个变量的空间复杂度为O(1)，需要额外申请一个等长数组的空间复杂度为O(n)，需要循环申请变量空间复杂度根据循环次数而定，比如循环logn次，每次申请数个变量，就是O (logn)。

2. 排序算法

为了方便记录，排序一律从小到大。

名称时间复杂度最好情况最坏情况空间复杂度稳定性
比较排序
选择排序O(n2)O(n2)O(n2)O(1)不稳定排序
冒泡排序O(n2)O(n)O(n2)O(1)稳定排序
插入排序O(n2)O(n)O(n2)O(1)稳定排序
希尔排序O(n1.5)O(n1.3)O(n2)O(1)不稳定排序
归并排序O(nlogn)O(nlogn)O(nlogn)O(n)

非原地排序

稳定排序
快速排序O(nlogn)O(nlogn)O(n2)O(logn)不稳定排序
堆排序O(nlogn)O(nlogn)O(nlogn)O(1)不稳定排序
非比较排序
计数排序O(n+k)O(n+k)O(n+k)O(k)

非原地排序

稳定排序
桶排序O(n+k)O(n+k)O(n2)O(n+k)

非原地排序

稳定排序
基数排序O(kn)O(kn)O(kn)O(n+k)

非原地排序

稳定排序

2.1 选择排序

选择排序的基本思想就是从数组中选出最小的那个数字，放在最前面，然后再选出第二小的，放在第二个位置，如此反复，一次选一个，直到排序完成。
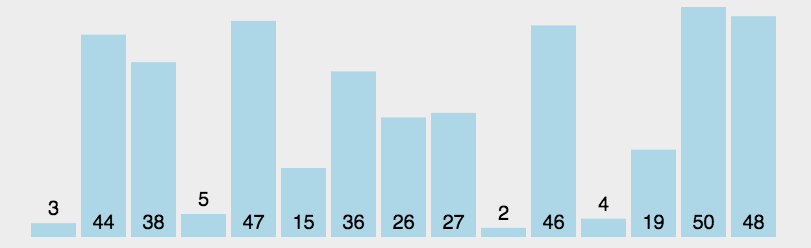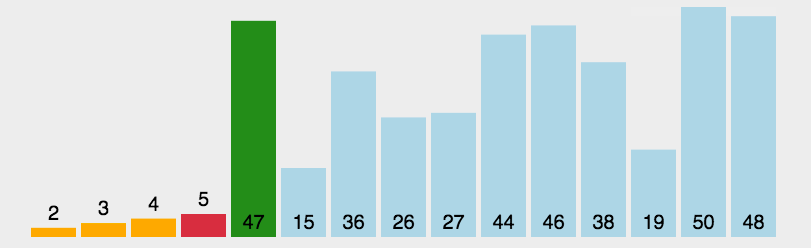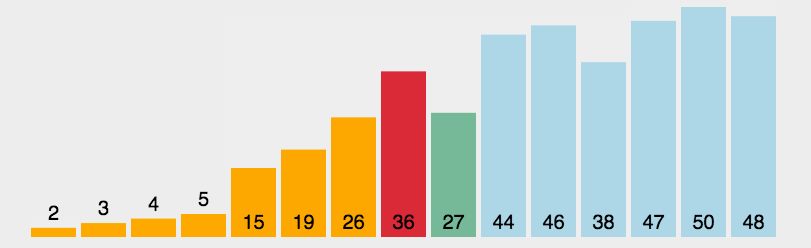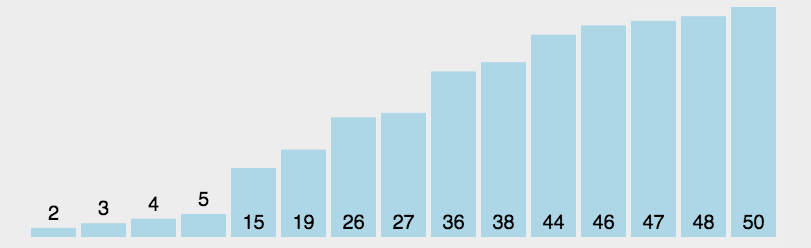
在这里插入图片描述
基本步骤：

  1. 将数组分成已排序（前面）和未排序（后面）两个部分。
  2. 已排序部分初始长度为0，未排序部分是数组长度。
  3. 每次循环，从未排序部分选出最小的一个数，放到已排序部分的后面。
  4. 已排序部分长度+1，未排序部分长度-1。
  5. 重复3，4步骤直到排序结束。

特点：

  • 不稳定排序，原地排序。
  • 时间复杂度O(n2)，空间复杂度O(1)。
  • 没有最好情况和最坏情况，无论何时效率都是O(n2)。

代码实现：

/**
 * 选择排序
 * 1. 将数组分成已排序（前面）和未排序（后面）两个部分
 * 2. 已排序部分初始长度为0，未排序部分是数组长度
 * 3. 每次循环，从未排序部分选出最小的一个数，放到已排序部分的后面
 * 4. 已排序部分长度+1，未排序部分长度-1
 * 5. 重复3，4步骤直到排序结束
 * @param array
 */
public static void selectSort(int[] array){
    int minIndex; //用于记录最小数字的下标
    for (int i=0; i<array.length; i++){
        minIndex = i;
        for (int j=i; j<array.length; j++){
            if (array[j] < array[minIndex]) //遍历整个未排序部分，找到最小数的下标
                minIndex = j;
        }
        int tem = array[minIndex];
        array[minIndex] = array[i];
        array[i] = tem;
    }
}

2.2 冒泡排序

冒泡排序从前往后进行扫描，在扫描的同时进行两两比较，并将大数放在后面，这样在扫描一轮之后，在最后的数一定是数组的最大值，然后再进行第二次扫描，将第二大的数放在倒数第二个，如此反复直到排序完成。
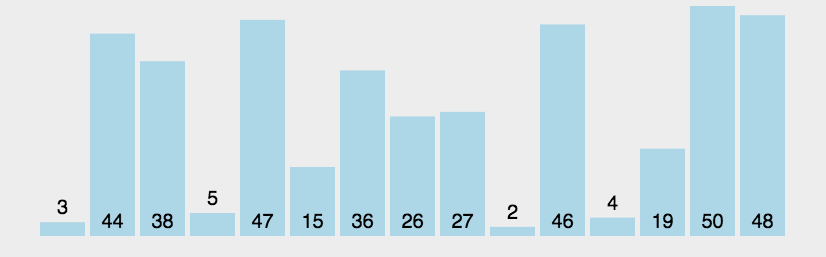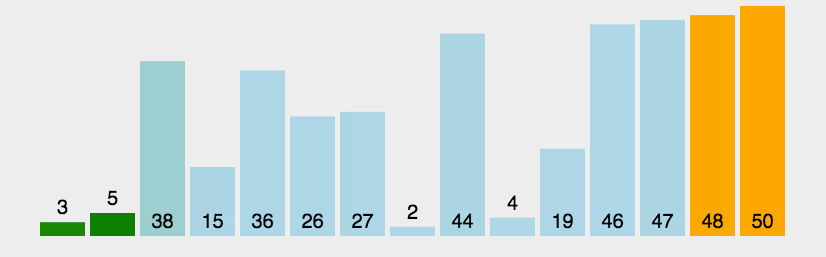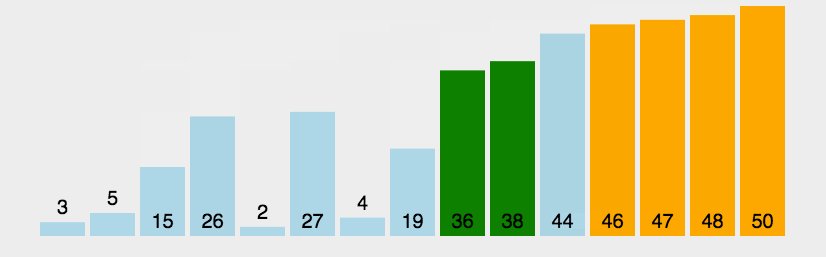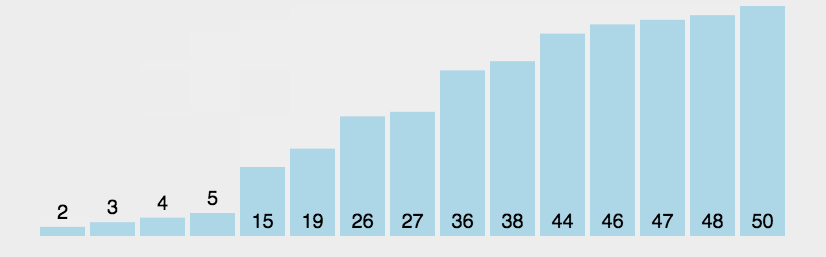
在这里插入图片描述

基本步骤：

  1. 将数组分成已排序（前面）和未排序（后面）两个部分
  2. 已排序部分初始长度为0，未排序部分是数组长度
  3. 从头到尾扫描未排序部分，并对数字进行两两比较，如果前面的数字大于后面的数字，则交换
  4. 在做完3之后，可以使未排序部分中的最大值在最后面，此时已排序部分长度+1，未排序部分长度-1
  5. 重复3，4步骤直到排序结束

特点：

  • 稳定排序，原地排序。
  • 时间复杂度O(n2)，空间复杂度O(1)。
  • 当一个数组在传入时就已经是排序完成的，此时是最好情况，时间复杂度O(n)，数字交换次数0。
  • 当一个数组在传入时是逆序的，此时是最坏情况，时间复杂度O(n2)，数字交换次数n*(n-1)/2。

代码实现：

/**
 * 冒泡排序
 * 1. 将数组分成已排序（前面）和未排序（后面）两个部分
 * 2. 已排序部分初始长度为0，未排序部分是数组长度
 * 3. 从头到尾扫描未排序部分，并对数字进行两两比较，如果前面的数字大于后面的数字，则交换它们
 * 4. 在做完3之后，可以使未排序部分中的最大值在最后面，此时已排序部分长度+1，未排序部分长度-1
 * 5. 重复3，4步骤直到排序结束
 * @param array
 */
public static int[] BubbleSort(int[] array){
    boolean sortFlag = false; //数字是否有交换的标记，false为未交换，true为有交换
    for (int i=0; i<array.length; i++){
        sortFlag = false;
        for (int j=0; j<array.length-1-i; j++){
            if (array[j] > array[j+1]){ //如果前面的数字大于后面的数字则交换它们
                int tem = array[j];
                array[j] = array[j+1];
                array[j+1] = tem;
                sortFlag = true;
            }
        }
        //这里是优化后的代码，在最好情况下可以使得冒泡排序的时间复杂度为O(n)
        if (!sortFlag)
            break;
    }
    return array;
}

关于改进冒泡排序的代码，参考这篇：
冒泡排序最佳情况的时间复杂度，为什么是O(n) - melon.h - 博客园
https://www.cnblogs.com/melon-h/archive/2012/09/20/2694941.html

2.3 插入排序

插入排序是假设数组的第一个数是已排序的，然后把第二个数当成新加入的数字，进行排序，再把第三个数加入和前面两个数一起排序，插入到已排序数组中的合适位置，如此反复直到排序结束。
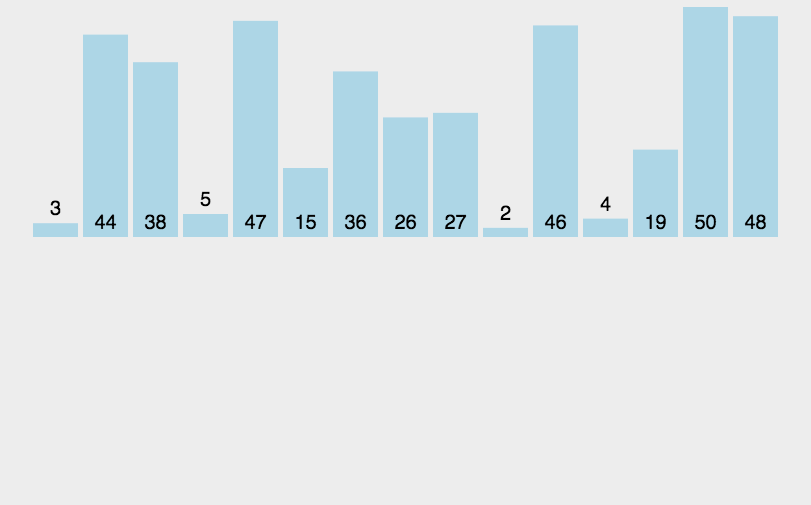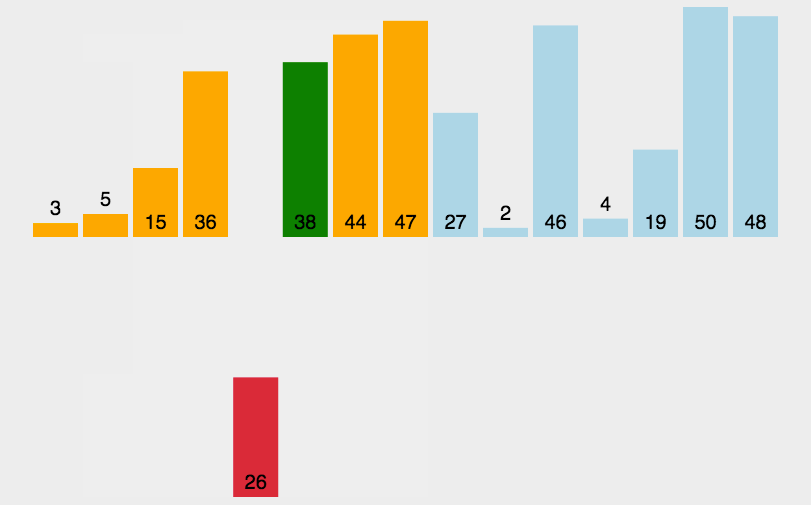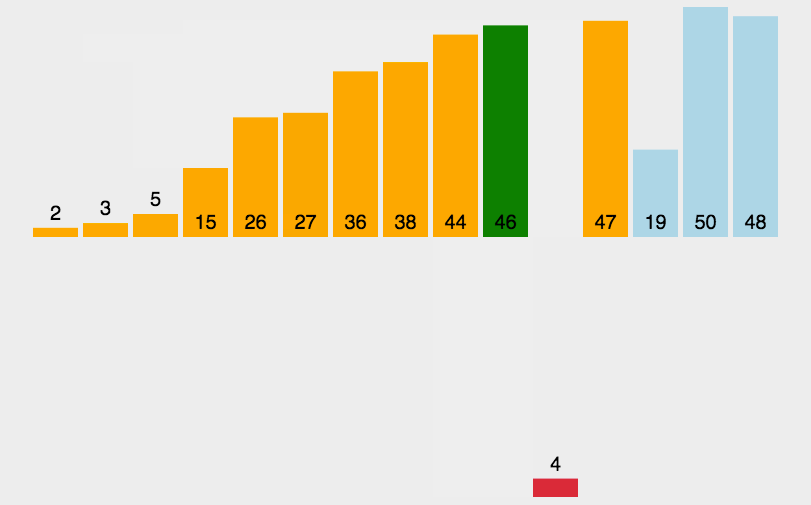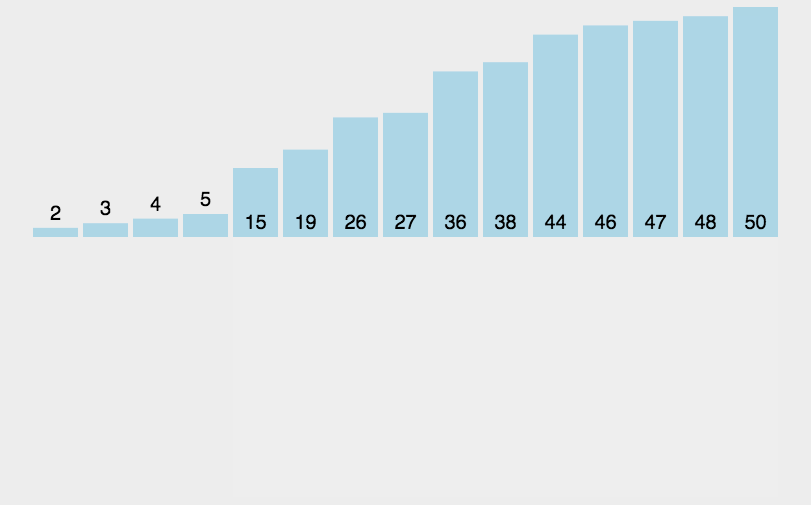
在这里插入图片描述
基本步骤：

  1. 将数组分成已排序（前面）和未排序（后面）两个部分
  2. 已排序部分初始长度为1，未排序部分是数组长度-1
  3. 将未排序的第一个数当成是要插入已排序部分的数，从后往前反复将要插入的数和已排序的数比较，如果已排序的数更大，则将其往后挪一位，直到要插入的数更大为止。
  4. 将要插入的数放入已排序部分的当前位置，然后已排序部分长度+1，未排序部分长度-1
  5. 重复3，4步骤直到排序结束。

特点：

  • 稳定排序，原地排序。
  • 时间复杂度O(n2)，空间复杂度O(1)。
  • 当一个数组在传入时就已经是排序完成的，此时是最好情况，时间复杂度O(n)，赋值次数0。
  • 当一个数组在传入时是逆序的，此时是最坏情况，时间复杂度O(n2)， 赋值次数n2 + 3n - 2。
  • 很明显可以看出，数据规模越小，数据基本有序程度越高，插入排序的效率就越高；反之如果数据规模很大而且并不是基本有序，那么赋值次数就会变得非常多，效率相对也会低下。

插入排序最好、最坏、平均情况时间复杂度分析 - 小新新的蜡笔 - 博客园
https://www.cnblogs.com/zsgyx/p/10464501.html
代码实现：

/**
 * 插入排序
 * 1. 将数组分成已排序（前面）和未排序（后面）两个部分
 * 2. 已排序部分初始长度为1，未排序部分是数组长度-1
 * 3. 将未排序的第一个数当成是要插入已排序部分的数，从后往前反复将要插入的数和已排序的数比较，如果已排序的数更大，则将其往后挪一位，直到要插入的数更大为止
 * 4. 将要插入的数放入已排序部分，然后已排序部分长度+1，未排序部分长度-1
 * 5. 重复3，4步骤直到排序结束。
 * @param array
 * @return
 */
public static int[] insertSort(int[] array){
    int inserted;
    for(int i=1; i<array.length; i++){
        if (array[i] < array[i-1]){  //这句是优化，可以使得最好情况时时间复杂度为O(n)
            inserted = array[i]; //取出当前要插入的数
            int j=i-1;
            for (; j>=0 && array[j] > inserted; j--){ //将当前数反复和数组的数比较，比它大的时候，数组的数往后挪。
                array[j+1] = array[j];
            }
            array[j+1] = inserted;
        }
    }
    return array;
}

2.4 希尔排序

当数组的规模很大的时候，插入排序就会因为要一直一个一个数挪动，而导致效率特别低下。就在这个时候，希尔排序出现了，他可以看成是插入排序的加强版，希尔排序不再一位一位的挪动数据，而是设置一个增量值，让数据一次性挪动好几位，来使得赋值的次数减少，快速完成排序。
在这里插入图片描述
基本步骤：

  1. 设置增量为数组长度的一半
  2. 将数组划分为多个有增量的小数组
  3. 让每个小数组进行插入排序
  4. 增量变成原先长度的一半
  5. 重复234步骤直到排序结束

特点：

  • 不稳定排序，原地排序。
  • 时间复杂度O(n1.3)，空间复杂度O(1)。
  • 当一个数组在传入时就已经是排序完成的，此时是最好情况，时间复杂度O(n)。
  • 希尔排序的最坏情况时间复杂度O(n1.5)，什么情况下会是最坏时间复杂度没找到。

代码实现：

    /**
     * 希尔排序
     * 1.本质是插入排序的变种，引入了增量的概念
     * 2.设置增量为数组长度的一半
     * 3.将数组划分为多个有间隔的小数组
     * 4.让每个小数组进行插入排序
     * 5.增量变成原先长度的一半
     * 6.重复234步骤直到排序结束
     * @param array
     * @return
     */
    public static int[] shellSort(int[] array){
    	// gap就是增量，初始为数组长度的一半
        for (int gap = array.length/2; gap>0; gap/=2){
            for (int i=gap; i< array.length; i++){
                insertI(array, gap, i); //进行插入排序
            }
        }
        return array;
    }

    /**
     * 本质是插入排序增量版，将插入排序中的1变成gap
     * @param array
     * @param gap 增量
     * @param i 要插入的数的下标
     */
    public static void insertI(int[] array, int gap, int i){
        if (array[i] < array[i-gap]) {
            int inserted = array[i];
            int j = i - gap;
            for (; j >= 0 && inserted < array[j]; j -= gap) {
                array[j + gap] = array[j];
            }
            array[j + gap] = inserted;
        }
    }

2.5 归并排序

归并排序主要是用了分治法的思想。

  • 分治法：先将问题分解为小的问题，小的问题再分解为更小的问题，这是分；将细分后的小问题解决得到的答案，合在一起，得到最终答案，这是治。

那么分治法如何运用到排序上呢？先将原本的数组二等分得到两个小数组，小数组再等分变成四个数组，一直分下去直到所有小数组都只有一个元素，那么所有小数组都是有序的，再将这些数组两两合并排序，一直合并最终得到一个大的有序数组。

虽然思想是先等分后再合并，但是实际上由于递归的特殊性，代码会每分出两个最小长度的数组就立刻执行合并，但是总体的思想还是没变。
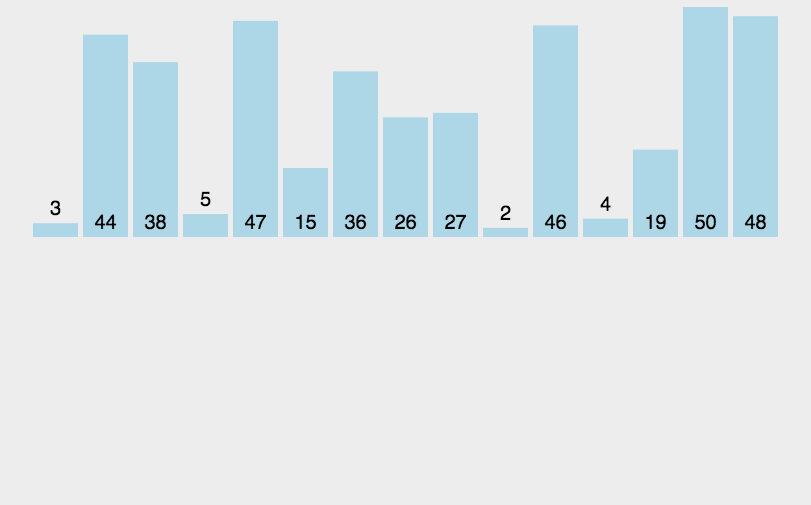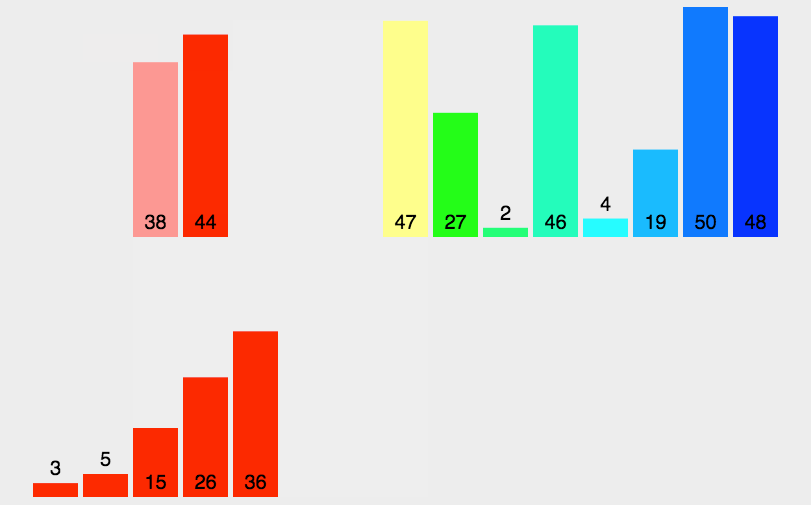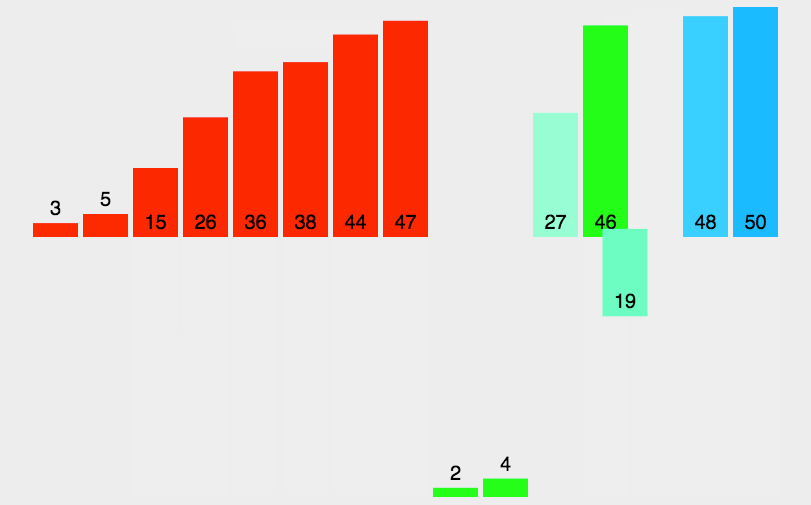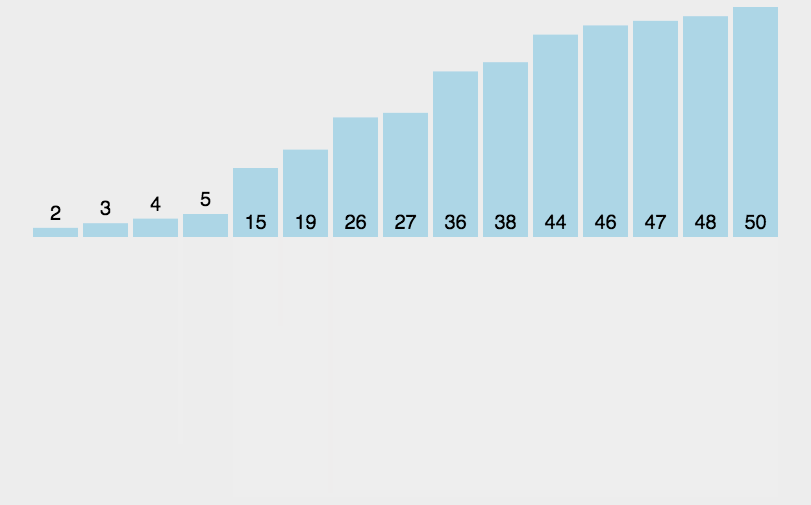
在这里插入图片描述
基本步骤（会用到递归）：

  1. 先将数组等分为两个小数组。
  2. 将得到的小数组继续等分，直到无法分解为止。
  3. 将分解后的数组依次合并，直到排序结束。

特点：

  • 稳定排序，非原地排序（因为排序时多开了一个数组）。
  • 时间复杂度O(nlogn)，空间复杂度O(n+logn)。
  • 由于使用了二分法，归并排序无论情况好坏都必定会花费O(nlogn)的时间。

代码实现：

/**
 * 归并排序
 * 1. 将数组无限二等分，得到无数长度为2-3的数组
 * 2. 再将这些小数组依次合并
 * 3. 有用到递归的思维
 * 4. 要注意，这个方法初始right的值为array.length-1，不然会越界
 * @param array 目标数组
 * @param left 最左边的下标
 * @param right 最右边的下标
 * @return
 */
private static int[] mergeSort(int[] array, int left, int right) {
    if (left < right){
        int mid = (left + right) / 2; //求出中间位置
        // 递归进行继续等分
        mergeSort(array, left, mid);
        mergeSort(array, mid + 1, right);
        // 等分之后进行合并，这里直接看代码不太容易看懂，因为用上了递归
        mergeArray(array, left, mid, right);
    }
    return array;
}

/**
 * 合并数组
 * array[left]到array[mid]是前面数组，array[mid+1]到array[right]是后面数组
 * @param array
 * @param left
 * @param mid
 * @param right
 */
private static void mergeArray(int[] array, int left, int mid, int right) {
    int[] temp = new int[right - left + 1]; // 这里建议在全局单独开一个数组反复使用，而不是重复开数组
    // l代表前面数组的下标，r代表后面数组的下标，k代表temp数组下标
    int l = left, r = mid + 1, k = 0;
    // 接下来合并数组，就是很简单的比较后合并
    while(l <= mid && r <= right){
        if (array[l] < array[r])
            temp[k++] = array[l++];
        else
            temp[k++] = array[r++];
    }
    while (l <= mid)
        temp[k++] = array[l++];
    while (r <= right)
        temp[k++] = array[r++];

    // 合并后的数组内容再复制回去
    for (int i=0; i<k; i++){
        array[left + i] = temp[i];
    }
}

接下来是非递归实现，在递归的过程中，我们先把原数组拆成无数小数组，如果用非递归的解法，就不需要分的过程，第一个小数组就是array[0]，第二个小数组就是array[1]，直接开始合并即可。

    /**
     * 归并排序非递归版
     * 1. 没有了分的过程，直接从小数组开始合。
     * @param array 目标数组
     * @return
     */
    private static int[] mergeSort(int[] array){
        // i代表该合并大小数组的长度，一开始为1，然后为2，4，直到整个数组长度
        for (int i=1; i< array.length; i += i){
            // 三个变量很好理解，就是前面数组和后面数组的下标
            int left = 0;
            int mid = left + i;
            int right = mid + i;
            while (right < array.length){
            	// 这个方法就是上面递归版时用到的方法，一模一样，用途是合并数组
                mergeArray(array, left, mid, right);
                // 在做完合并之后，三个变量往后移，进行下一次的合并
                left = right + 1;
                mid = left + i;
                right = mid + i;
            }

            //合并之后会会有遗漏的部分，再合并一次
            if (mid < array.length - 1){
                mergeArray(array, left, mid, array.length - 1);
            }
        }
        return array;
    }

2.6 快速排序

最常见的算法，Java和C的内置sort方法都是用快速排序实现的，和归并排序一样用上了分治法的思想。
它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
在这里插入图片描述
注：我的解法是将左边第一个数作为基准值，和图片不符，不过思路是一样的。
由于这张图有明确出处，放上原作者地址：
https://www.cnblogs.com/fivestudy/p/10012193.html

基本步骤：

  • 递归：
  1. 设定一个基准值，把他放到数组的中间某个位置
  2. 使得左边的数都小于这个基准值，右边的数都大于这个基准值
  3. 对基准值左边的子数组和右边的子数组再进行一次快速排序
  4. 3是递归过程，结束条件是子数组的长度为1，递归结束时，排序结束。
  • 如何达成递归的1和2：
  1. 将第一个数作为基准值，然后数组左右两边设置一个下标变量
  2. 下标变量分别从左往右，和从右往左进行扫描
  3. 左边下标变量从左往右扫描直到当前数大于基准数时停止
  4. 右边下标变量从右往左扫描直到当前数小于基准数时停止
  5. 交换左右下标变量此时所在的值
  6. 重复2345直到左边下标等于右边下标，
  7. 交换第一个数（基准值）和左边下标或者右边下标所指的值。

特点：

  • 不稳定排序，原地排序。
  • 时间复杂度O(nlogn)，空间复杂度O(logn)（每次递归都会开几个变量，递归logn次）。
  • 当每次划分子数组都正好分成两个相同大小的子数组时，达到最好情况，时间复杂度为O(nlogn)。
  • 当每次划分子数组时都有一个子数组的长度为0（数组本身为正序或者逆序）时，达到最坏情况，时间复杂度O(n2)。

代码实现：

    /**
     * 快速排序
     * 不同于C语言的标准解法，这边将快速排序分为了两个方法
     * 使用了递归的思路。
     *
     * 1. 设定一个基准值，把他放到数组的中间某个位置
     * 2. 使得左边的数都小于这个基准值，右边的数都大于这个基准值
     * 3. 对基准值左边的子数组和右边的子数组再进行一次快速排序
     * 4. 3是递归过程，结束条件是子数组的长度为1，递归结束时，排序结束。
     *
     * @param array 目标数组
     * @param left 最左边数的下标
     * @param right 最右边数的下标
     * @return 结果数组
     */
    public static int[] quickSort(int[] array, int left, int right){
        if (left < right){
            int mid = partition(array, left, right);  // 求出分割基准值的下标

            quickSort(array, left, mid-1);
            quickSort(array, mid+1, right);
        }
        return array;
    }


    /**
     * 分割数组，并求出基准值的下标
     * 1. 将第一个数作为基准值，然后数组左右两边设置一个下标变量
     * 2. 下标变量分别从左往右，和从右往左进行扫描
     * 3. 左边下标变量从左往右扫描直到当前数大于基准数时停止
     * 4. 右边下标变量从右往左扫描直到当前数小于基准数时停止
     * 5. 交换左右下标变量此时所在的值
     * 6. 重复2345直到左边下标等于右边下标，
     * 7. 交换第一个数（基准值）和左边下标或者右边下标所指的值
     *
     * 这个方法有两个重点
     * 1. int l = left，不能l = left + 1，一定要将自己也列入比较范围之中
     *    不然如果传入的数组长度为2的话，就会直接交换，而不是比较后决定是否交换
     *
     * 2. 如果你是将第一个数作为基准值pivot的话，那么你的两个while方法，一定要
     *    第一个是从右往左，第二个是从左往右，这样才能保证扫描到最后的中间值
     *    比pivot小
     *
     *    同理，如果你是将最后一个数作为基准值pivot，那么第一个while应该要从左往右
     *    第二个while从右往左，以保证最后得出的中间值比pivot大
     *
     * @param array 目标数组
     * @param left 最左边数的下标
     * @param right 最右边数的下标
     * @return 基准值的下标
     */
    public static int partition(int[] array, int left, int right){
        int pivot = array[left]; //第一个数就是基准值

        int l = left;  // l为左边下标，r为右边下标
        int r = right;
        while (l < r){
            
            while (l < r && array[r] >= pivot) // 从右往左扫描，找到小于基准值的数时停止扫描
                r--;
            while (l < r && array[l] <= pivot) // 从左往右扫描，找到大于基准值的数时停止扫描
                l++;
            
            int temp = array[l];
            array[l] = array[r];
            array[r] = temp;
        }
        
        array[left] = array[r];
        array[r] = pivot;

        return r;
    }

2.7 堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

完全二叉树：是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

简单来说，完全二叉树就是一个满二叉树（最后一层没有子节点，其他层满节点）在最后一层从右到左去掉n个叶子节点的二叉树。
在这里插入图片描述
接下来说堆，堆是一个满足了特殊条件的完全二叉树，当完全二叉树上每个节点的值，都小于（大于）它的父节点时，这个完全二叉树就被称为最大（小）堆。
在这里插入图片描述
那么，知道了堆的特性，也知道了堆是一个完全二叉树，这要怎么和我们的数组结合起来呢？是这样，当一个二叉树他是完全二叉树（或者满二叉树）的时候，他是可以直接用一维数组表示的（而不是用链表）。

这种情况下，这个二叉树满足一个公式：

  • 任意一个节点array[x]的左子树为array[x2 + 1]，右子树为array[x2 + 2]。

再套入堆的特性有（这里以最大堆为例）：

  • array[x] >= array[x*2 + 1]
  • array[x] >= array[x*2 + 2]
    在这里插入图片描述

那么，在知道了这么多内容后，如何将这个堆和排序整合在一起呢？

具体步骤（从小到大用最大堆，这里以它为例）：

  1. 将目标数组当成一个完全二叉树。
  2. 将从倒数第一个非叶子节点开始，从右到左，从下到上的将二叉树调整成最大堆（下沉）。
  3. 将堆顶的元素和最后一个叶子元素交换（因为堆顶的元素肯定是最大值，放到最后面）。
  4. 将交换后的叶子元素移出最大堆（把他当做不存在）。
  5. 剩余部分不再是堆结构，重新调整成最大堆（下沉）。
  6. 第4步每移出一个数，就代表排序完成一个数。重复345直到排序结束。

最后一个问题，如何调整二叉树使其成为堆，简单来说二叉堆（也就是我们的最大堆）建立，增加，删除元素一般都是通过下沉和上浮两个操作来执行，由于堆排序用不到上浮，这里就介绍下沉的具体思路：

  1. 从目标节点的两个叶子节点中选出较小的那个。
  2. 将目标节点和其进行比较。
  3. 如目标节点较小，则两者位置交换，并对交换后的叶子节点继续执行12步骤。
  4. 如目标节点较大，则调整结束。

特点：

  • 非稳定排序，原地排序。
  • 时间复杂度O(nlogn)，空间复杂度O(1)。
  • 堆排序是一个效率稳定的排序算法，无论情况好坏它的时间复杂度都控制在O(nlogn)。
  • 创建堆消耗时间O(n)，取出堆顶n次O(n)，对新堆顶进行下沉n次O(nlogn)，总共消耗时间O(2n+nlogn)，时间复杂度为O(nlogn)。

代码实现（请务必要看，基本上每一行都注释了）：

/** 
 * 堆排序
 * 1. 将目标数组当成一个完全二叉树。
 * 2. 将从倒数第一个非叶子节点开始，从右到左，从下到上的将二叉树调整成最大堆。
 * 3. 将堆顶的元素和最后一个叶子元素交换（因为堆顶的元素肯定是最大值，放到最后面）。
 * 4. 将交换后的叶子元素移出最大堆（把他当做不存在）。
 * 5. 剩余部分不再是堆结构，重新调整成最大堆。
 * 6. 第4步每移出一个数，就代表排序完成一个数。重复345直到排序结束。
 * @param array 目标数组
 * @return 结果数组
 */
public static int[] heapSort(int[] array) {

    for (int i=array.length/2-1; i>=0; i--){
        // 从倒数第一个非叶子节点开始，从右到左，从下到上调整二叉树，从而创建堆
        downHeap(array, i, array.length-1);
    }

    for (int i=array.length-1; i>0; i--){
        // 取出堆顶，堆的大小-1
        int temp = array[i];
        array[i] = array[0];
        array[0] = temp;

        // 对换上去的新堆顶进行下沉
        downHeap(array, 0, i);
    }
    return array;

}

/**
 * 堆的下沉
 * 1. 从目标节点的两个叶子节点中选出较小的那个。
 * 2. 将目标节点和其进行比较。
 * 3. 如目标节点较小，则两者位置交换，并对交换后的叶子节点继续执行12步骤。
 * 4. 如目标节点较大，则调整结束。
 *
 * @param array 目标数组
 * @param target 目标节点
 * @param length 堆的大小，而不是数组的长度（堆的大小会因为数组排序完成而慢慢减少）
 */
public static void downHeap(int[] array, int target, int length){
	//每次循环开始时，变量i都是左子叶节点的下标
    for (int i=target*2+1;; i<length; i=i*2+1){

        // 选出左右子节点中较小的节点（前提是有两个节点）
        if (array[i] < array[i+1] && i+1 < length)
            i++;

        // 如果子节点大于父节点，则交换他们，并进行下一轮的比较
        // 这部分有更简单的写法，但是不利于整理思路，所以没有使用
        if (array[i] > array[target]){
            int temp = array[i];
            array[i] = array[target];
            array[target] = temp;

            // 交换后的子节点成为新的目标节点
            target = i;
        }
        // 如果子节点较小，那么调整结束
        else
            break;
    }
}

2.8 计数排序

最简单也是最有意思的一种排序方法，先统计数组中每个数出现的次数，然后根据数出现的次数从小到大再把数一个个再摆回去。

使用前提：已知数的最大值和最小值且它们的差值不能太大。
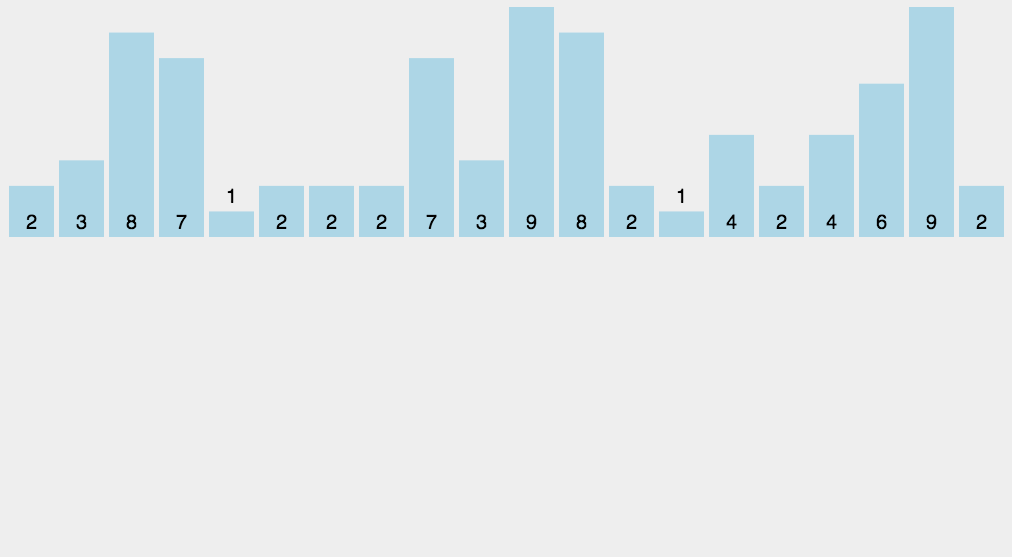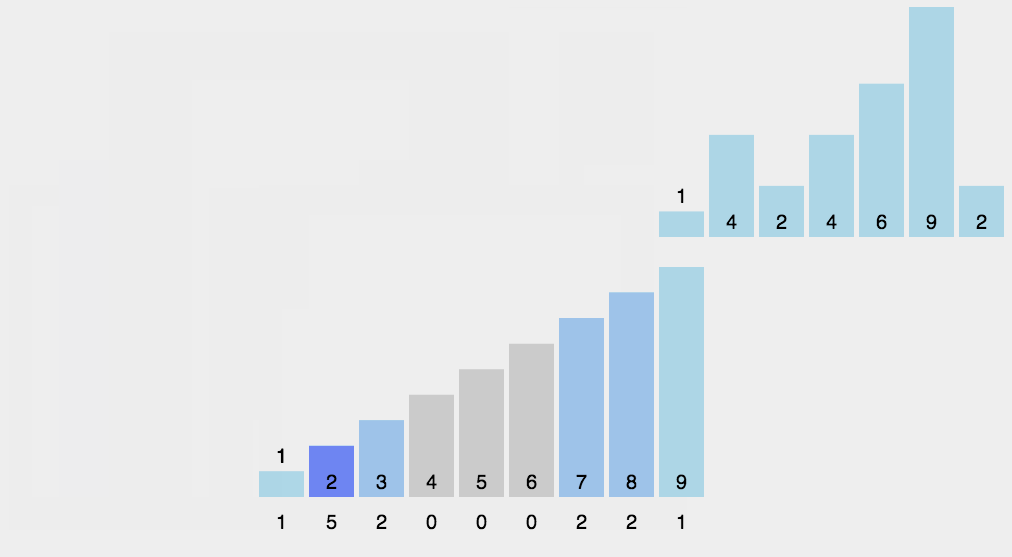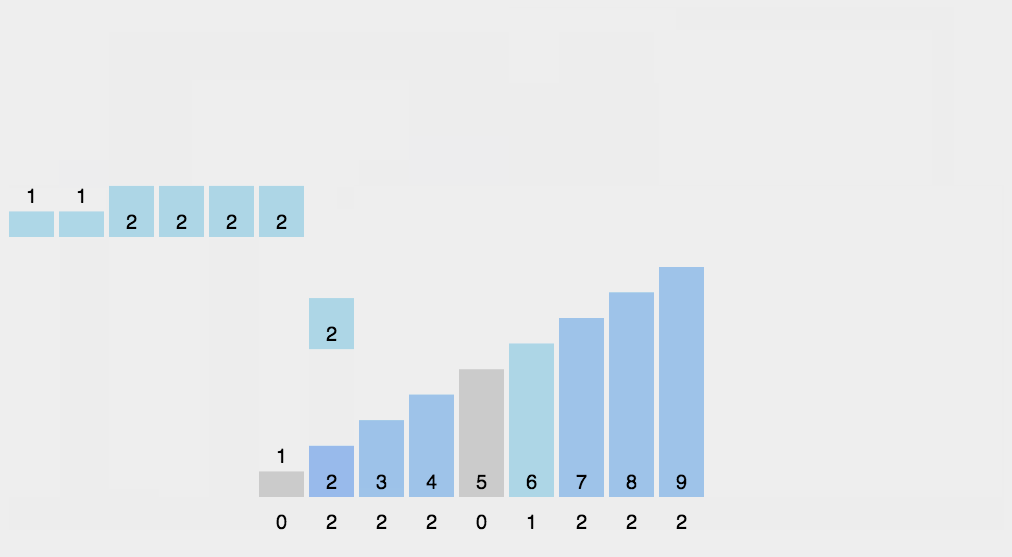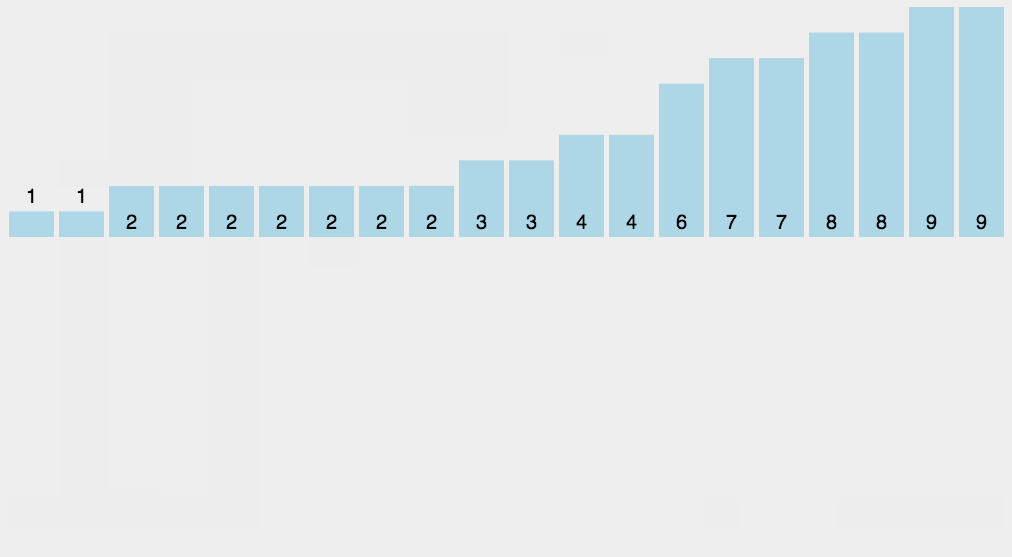
在这里插入图片描述
基本步骤：

  1. 新开一个数组用于统计目标数组中每个数出现的个数。
  2. 根据每个数出现的个数从头开始把数赋值回目标数组。

特点：

  • 稳定排序，非原地排序。
  • 时间复杂度O (n+k)，空间复杂度O(k)，k为最大值与最小值的差值。
  • 当最大值与最小值差值过大时，效率较差，差值较小时，效率较好，但都是O(n+k)。
  • 少见的非比较排序。

代码实现：

/**
 * 计数排序
 * 1. 新开一个数组用于统计目标数组中每个数出现的个数。
 * 2. 根据每个数出现的个数从头开始把数赋值回目标数组。
 * 3. 对于temp数组，temp[0]用于存放目标数组中的最小值（不一定是0，根据题目而定）
 * @param array 目标数组
 * @return 结果数组
 */
public static int[] countSort(int[] array){
    // 创建新数组，数组的大小是你最大值最小值的差值
    int[] temp = new int[100];

    // 统计数出现的个数
    for (int i=0; i<array.length; i++){
        temp[array[i]]++;
    }

    // 把数一个个重新赋值回去
    int t=0;
    for (int i=0; i<100; i++){
        while(temp[i] > 0){
           array[t++] = i;
           temp[i]--;
        }
    }
    return array;
}

2.9 桶排序

计数排序的升级版，简单来说就是计数排序时划分的区间不再只存放一个数，而是存放数据相近的一组数组（区间），然后每组数据在其内部排序之后，再整合成原本的目标数组。

用之前先回顾一下计数排序的两个缺点：

  1. 差值过大时不能使用计数排序（效率较差）。
  2. 数据精度较高时不能用计数排序（比如0-10的之内的双精度数据排序如2.3，4.6这样）。

那么桶排序如何对这两点进行改进呢，就是用上了区间的方法，把最大值和最小值之间的数进行瓜分，例如分成 5 个区间，5个区间对应5个桶，我们把各元素放到对应区间的桶中去，再对每个桶中的数进行排序，可以采用归并排序，也可以采用快速排序之类的。
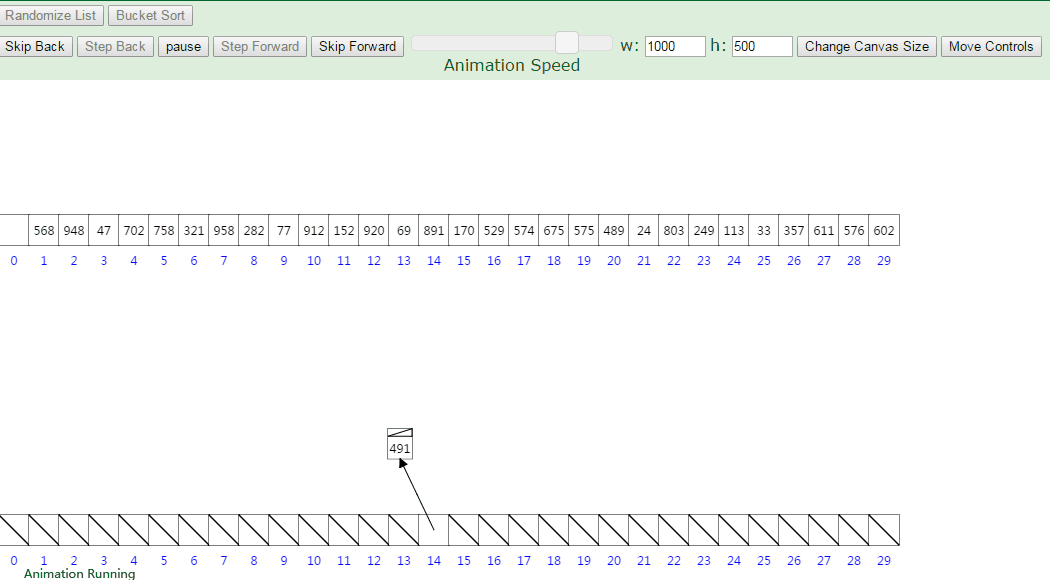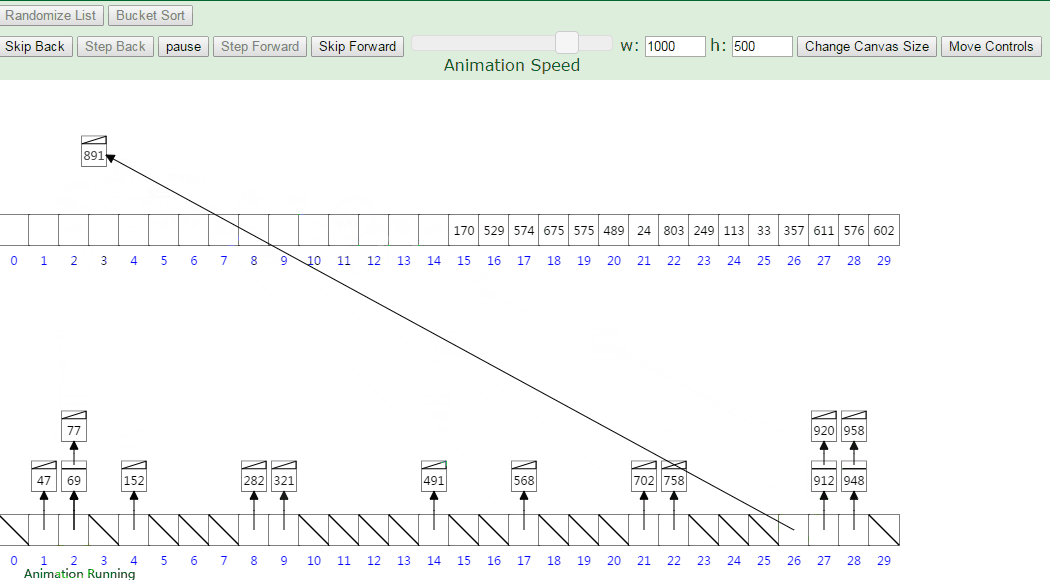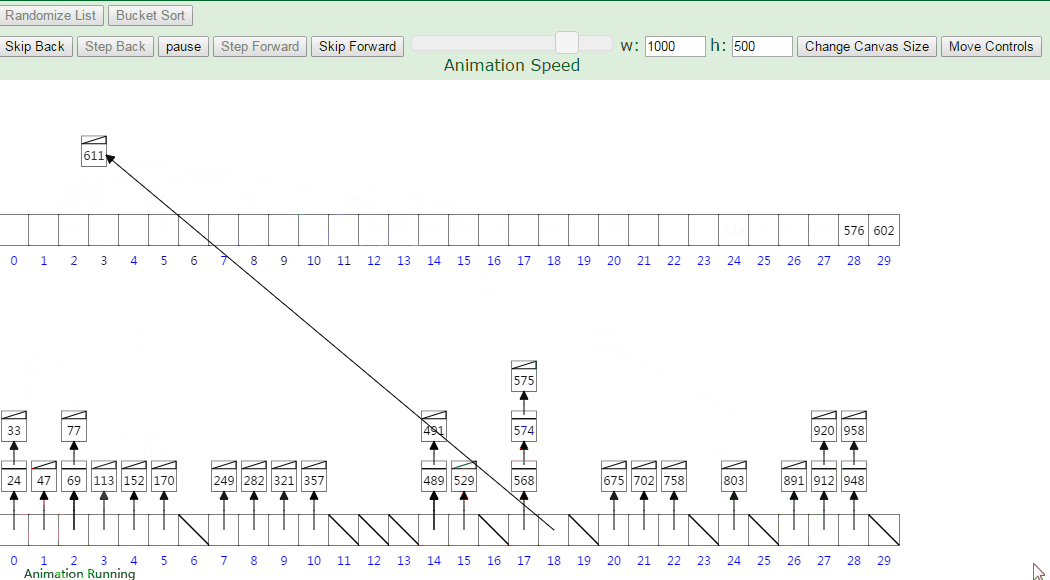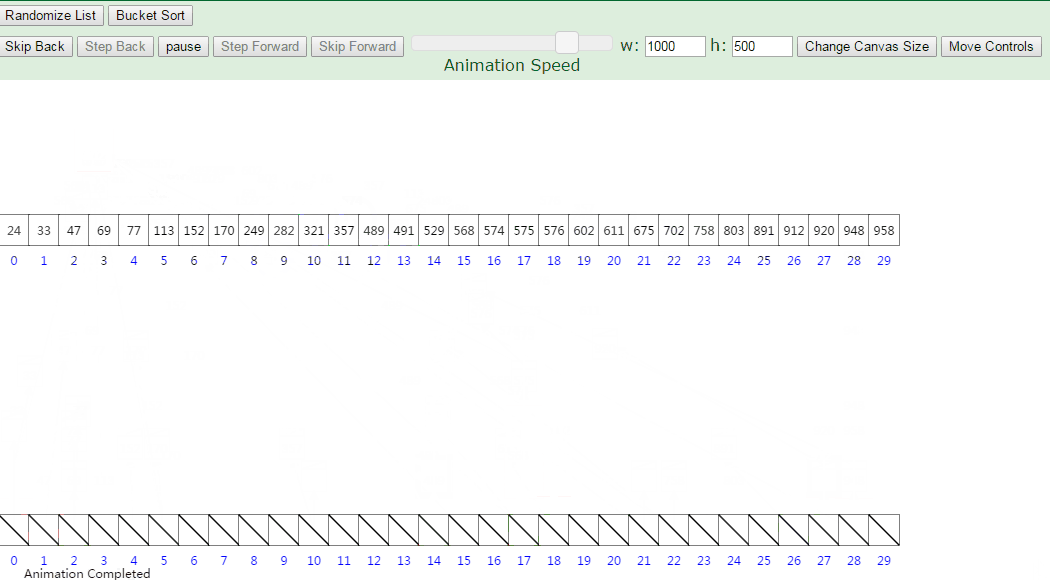
在这里插入图片描述
基本步骤：

  1. 算出最大值和最小值的差值
  2. 创建对应数量的桶
  3. 依次往桶里面存数据
  4. 每个桶各自排序
  5. 每个桶依次取出数据

特点：

  • 稳定排序，非原地排序。
  • 时间复杂度O(n+k)，时间复杂度O(n+k)。
  • 当一个桶存放了大量数据，而其他桶基本不存数据时（比如99个1和1个100），接近最坏情况，时间复杂度是O(n2)。
  • 当每个桶都存放了数量相近的数据时，接近最好情况，时间复杂度O(n+k)。
  • 少见的非比较排序。

代码实现：

/**
 * 桶排序
 * 1. 算出最大值和最小值的差值
 * 2. 创建对应数量的桶
 * 3. 依次往桶里面存数据
 * 4. 每个桶各自排序
 * 5. 每个桶依次取出数据
 * @param array 目标数据
 * @param bucketNum 桶的数量（也可以在方法内部设定）
 * @return
 */
public static int[] bucketSort(int[] array, int bucketNum) {
    // 先简单的算出最大值和最小值
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (int i=0; i<array.length; i++){
        if (min > array[i]) min = array[i];
        if (max < array[i]) max = array[i];
    }

    int d = max - min; // 最大值和最小值的差值
    int  div = d/(bucketNum-1); // 每个桶存放数的区间大小

    // 初始化数组（这里用ArrayList），数组内的每个元素都是桶（这里用LinkedList链表）
    ArrayList<LinkedList<Integer>> list = new ArrayList<>();
    for (int i=0; i<bucketNum; i++){
        list.add(new LinkedList<>());
    }

    // 开始存入元素（每个桶存入后是未排序的）
    for (int i=0; i<array.length; i++){
        list.get((array[i]-min)/div).add(array[i]);
    }

    // 每个桶各自排序（排序就用了他内置的方法，你也可以用别的方法）
    for (int i=0; i<bucketNum; i++){
        list.get(i).sort(null);
    }

    // 每个桶依次取出数据
    int t = 0;
    for (int i=0; i<bucketNum; i++){
        for (int j=0; j<list.get(i).size(); j++)
            array[t++] = list.get(i).get(j);
    }

    return array;
}

2.10 基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。
在这里插入图片描述

基本步骤：

  1. 找出数组的最大数，并求出有几位数
  2. 创建对应数量的桶（这里是十进制数据，所以是10个桶）
  3. 从低位开始，以该位数的值为基准，依次从桶里存数据
  4. 再按桶的顺序取出数放回原数组
  5. 位数+1（如个位变成十位，十位变成百位），重复34直到排序结束

特点：

  • 稳定排序，非原地排序。
  • 时间复杂度O(kn)，空间复杂度（n+k）。
  • 在最好情况和最坏情况下时间复杂度都是O(kn)。
  • 少见的非稳定排序。

代码实现：

/**
 * 桶排序
 * 1. 算出最大值和最小值的差值
 * 2. 创建对应数量的桶
 * 3. 依次往桶里面存数据
 * 4. 每个桶各自排序
 * 5. 每个桶依次取出数据
 * @param array 目标数据
 * @param bucketNum 桶的数量（也可以在方法内部设定）
 * @return
 */
public static int[] bucketSort(int[] array, int bucketNum) {
    // 先简单的算出最大值和最小值
    int min = Integer.MAX_VALUE;
    int max = Integer.MIN_VALUE;
    for (int i=0; i<array.length; i++){
        if (min > array[i]) min = array[i];
        if (max < array[i]) max = array[i];
    }

    int d = max - min; // 最大值和最小值的差值
    int  div = d/(bucketNum-1); // 每个桶存放数的区间大小

    // 初始化数组（这里用ArrayList），数组内的每个元素都是桶（这里用LinkedList）
    ArrayList<LinkedList<Integer>> list = new ArrayList<>();
    for (int i=0; i<bucketNum; i++){
        list.add(new LinkedList<>());
    }

    // 开始存入元素（每个桶存入后是未排序的）
    for (int i=0; i<array.length; i++){
        list.get((array[i]-min)/div).add(array[i]);
    }

    // 每个桶各自排序
    for (int i=0; i<bucketNum; i++){
        list.get(i).sort(null);
    }

    // 每个桶依次取出数据放回原数组
    int t = 0;
    for (int i=0; i<bucketNum; i++){
        for (int j=0; j<list.get(i).size(); j++)
            array[t++] = list.get(i).get(j);
    }

    return array;
}

参考材料

十大经典排序算法（动图演示） - 一像素 - 博客园
https://www.cnblogs.com/onepixel/articles/7674659.html
必学十大经典排序算法，看这篇就够了(附完整代码/动图/优质文章)(修订版)
https://mp.weixin.qq.com/s/IAZnN00i65Ad3BicZy5kzQ
图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园
https://www.cnblogs.com/chengxiao/p/6194356.html
图解排序算法(三)之堆排序 - dreamcatcher-cx - 博客园
https://www.cnblogs.com/chengxiao/p/6129630.html
算法：排序算法之桶排序_Java_7-SEVENS-优快云博客
https://blog.youkuaiyun.com/developer1024/article/details/79770240

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值