粒子群优化算法

1.算法简介

粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。它可以被纳入多主体优化系统(Multiagent Optimization System, MAOS).粒子群优化算法是由Eberhart博士和kennedy博士发明。
PSO模拟鸟群的捕食行为。一群鸟在随机搜索食物，在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻离食物最近的鸟的周围区域。
PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解，在每一次叠代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest，另一个极值是整个种群找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分最优粒子的邻居，那么在所有邻居中的极值就是局部极值。

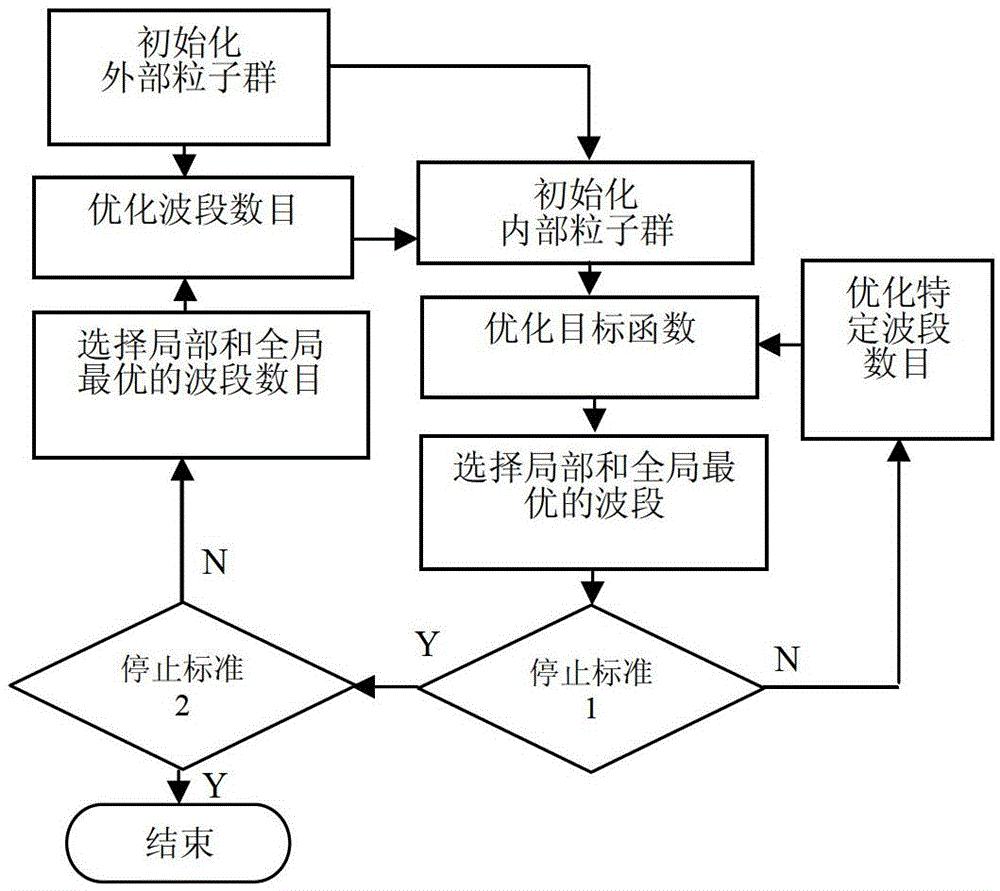
2.算法原理与步骤

原理

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

步骤

(1)初始化一群微粒（群体规模为m），包括随机的位置和速度；
  (2)评价每个微粒的适应度；
  (3)对每个微粒，将它的适应值和它经历过的最好位置pbest的作比较，如果较好，则将其作为当前的最好位置pbest；
  (4)对每个微粒，将它的适应值和全局所经历最好位置gbest的作比较，如果较好，则重新设置gbest的索引号；
  (5)变化微粒的速度和位置；
  (6)如未达到结束条件（通常为足够好的适应值或达到一个预设最大代数Gmax），回到ii）。

3.代码

PSO.m

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的三个参数
c1 = 1.49445;%加速因子
c2 = 1.49445;
w=0.8   %惯性权重

maxgen=1000;   % 进化次s数  
sizepop=200;   %种群规模

Vmax=1;       %限制速度围
Vmin=-1;     
popmax=5;    %变量取值范围
popmin=-5;
dim=10;       %适应度函数维数

func=1;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(func);%画出待优化的函数，只画出二维情况作为可视化输出

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,dim);    %初始种群
    V(i,:)=Vmax*rands(1,dim);             %初始化速度
                                     %计算适应度
    fitness(i)=fun(pop(i,:),func);   %粒子的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);   %全局最佳
pbest=pop;                %个体最佳
fitnesspbest=fitness;     %个体最佳适应度值
fitnessgbest=bestfitness; %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    fprintf('第%d代，',i);
    fprintf('最优适应度%f\n',fitnessgbest);
    for j=1:sizepop
        
        %速度更新
        V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:)); %根据个体最优pbest和群体最优gbest计算下一时刻速度
        V(j,find(V(j,:)>Vmax))=Vmax;   %限制速度不能太大
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);       %位置更新
        pop(j,find(pop(j,:)>popmax))=popmax;%坐标不能超出范围
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        if rand>0.98                         %加入变异种子，用于跳出局部最优值
            pop(j,:)=rands(1,dim);
        end
        
        %更新第j个粒子的适应度值
        fitness(j)=fun(pop(j,:),func); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnesspbest(j)
            pbest(j,:) = pop(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnessgbest
            gbest = pop(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i)=fitnessgbest;    
        
end
%% 结果分析
figure;
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

PSOMutation.m

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=500;   % 进化次数  
sizepop=100;   %种群规模

Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=5*rands(1,2);    %初始种群
    V(i,:)=rands(1,2);  %初始化速度
    %计算适应度
    fitness(i)=fun(pop(i,:));   %染色体的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    for j=1:sizepop
        
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        if rand>0.98     
            pop(j,:)=rands(1,2);
        end
        
        %适应度值
        fitness(j)=fun(pop(j,:)); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end 
    yy(i)=fitnesszbest;    
        
end
%% 结果分析
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

Drawfunc.m

function Drawfunc(label)

x=-5:0.05:5;%41列的向量
if label==1
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==2
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Schaffer([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

if label==3
    y = x;
    [X,Y] = meshgrid(x,y);
    [row,col] = size(X);
    for  l = 1 :col
         for  h = 1 :row
            z(h,l) = Griewank([X(h,l),Y(h,l)]);
        end
    end
    surf(X,Y,z);
    shading interp 
    xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis'); 
    title('mesh'); 
end

fun.m

function y = fun(x,label)
%函数用于计算粒子适应度值
%x           input           输入粒子 
%y           output          粒子适应度值 
if label==1
    y=Rastrigin(x);
elseif label==2
    y=Schaffer(x);
else
    y= Griewank(x);
end

fun1.m

function y = fun(x)
%函数用于计算粒子适应度值
%x           input           输入粒子 
%y           output          粒子适应度值 

y=-20*exp(-0.2*sqrt((x(1)^2+x(2)^2)/2))-exp((cos(2*pi*x(1))+cos(2*pi*x(2)))/2)+20+exp(1);

%y=x(1)^2-10*cos(2*pi*x(1))+10+x(2)^2-10*cos(2*pi*x(2))+10;

Griewank.m

function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人：
%编制日期：
[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
    y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;

Rastrigin.m

function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人：
% 编制日期：
[row,col] = size(x);
if  row > 1 
    error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;

Schaffer.m

function y=Schaffer(x)

[row,col]=size(x);
if row>1
    error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;

4.运行结果及分析

一、运行结果
（1）测试w,c1,c2，迭代次数为1000，优化函数为Rastrigin
①：c1 = 1.49445;
c2 = 1.49445;
w=0.8



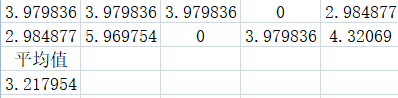
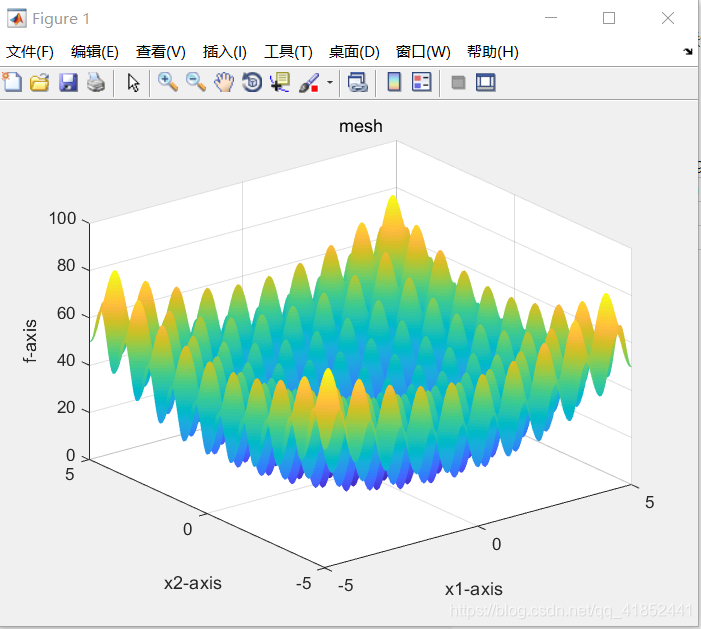
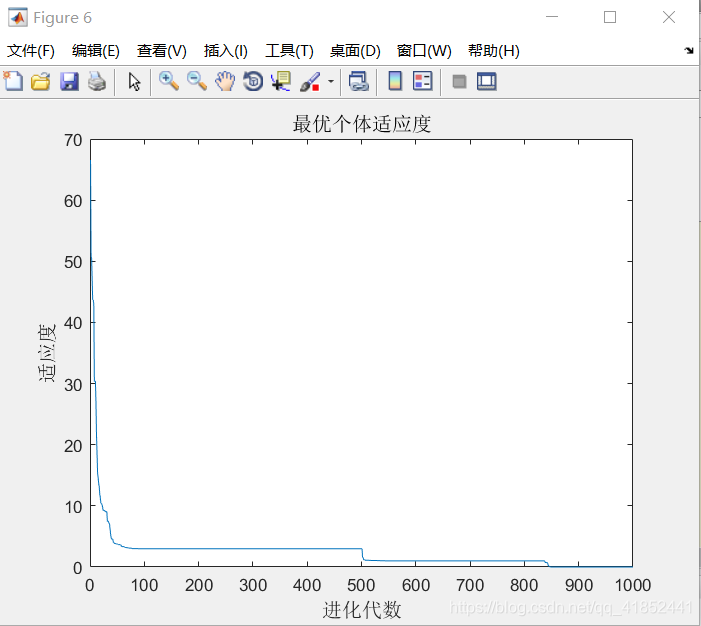
②：c1 = 1.9;
c2 = 1.1;
w=0.5


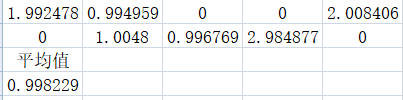
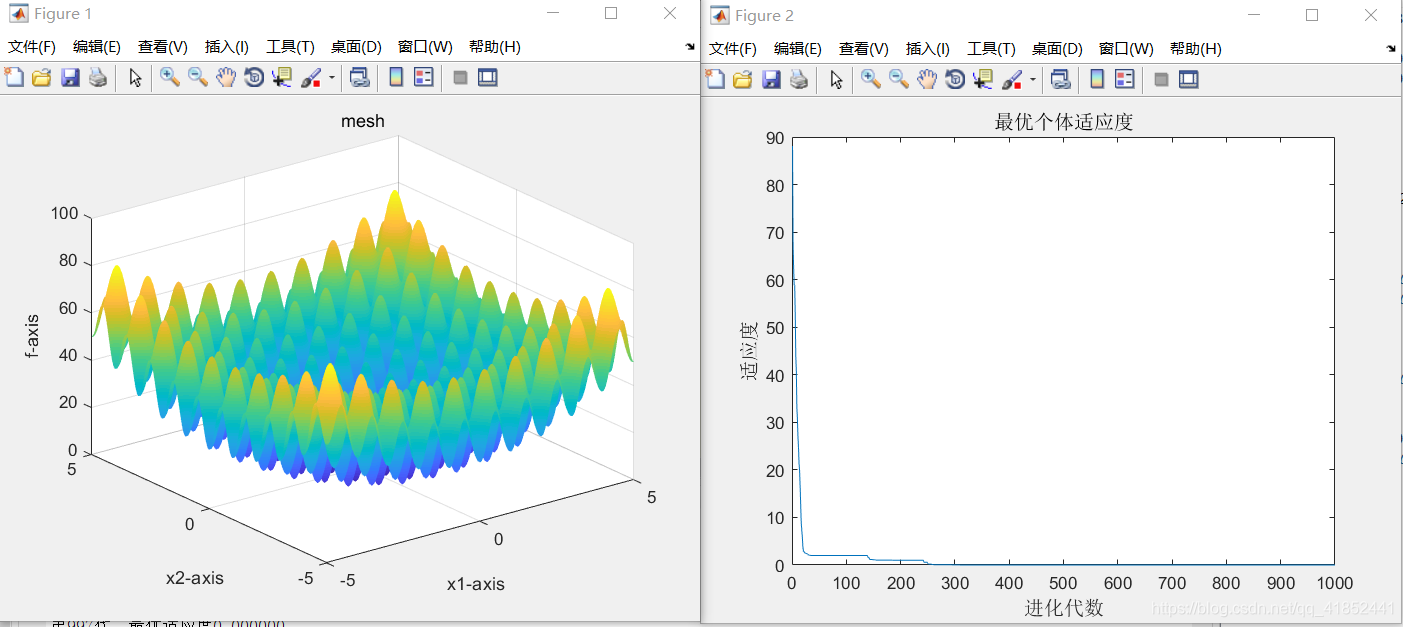
③：c1=1.7
c2=1.3
w=0.2


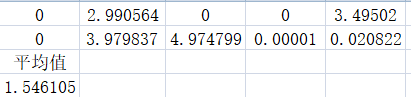
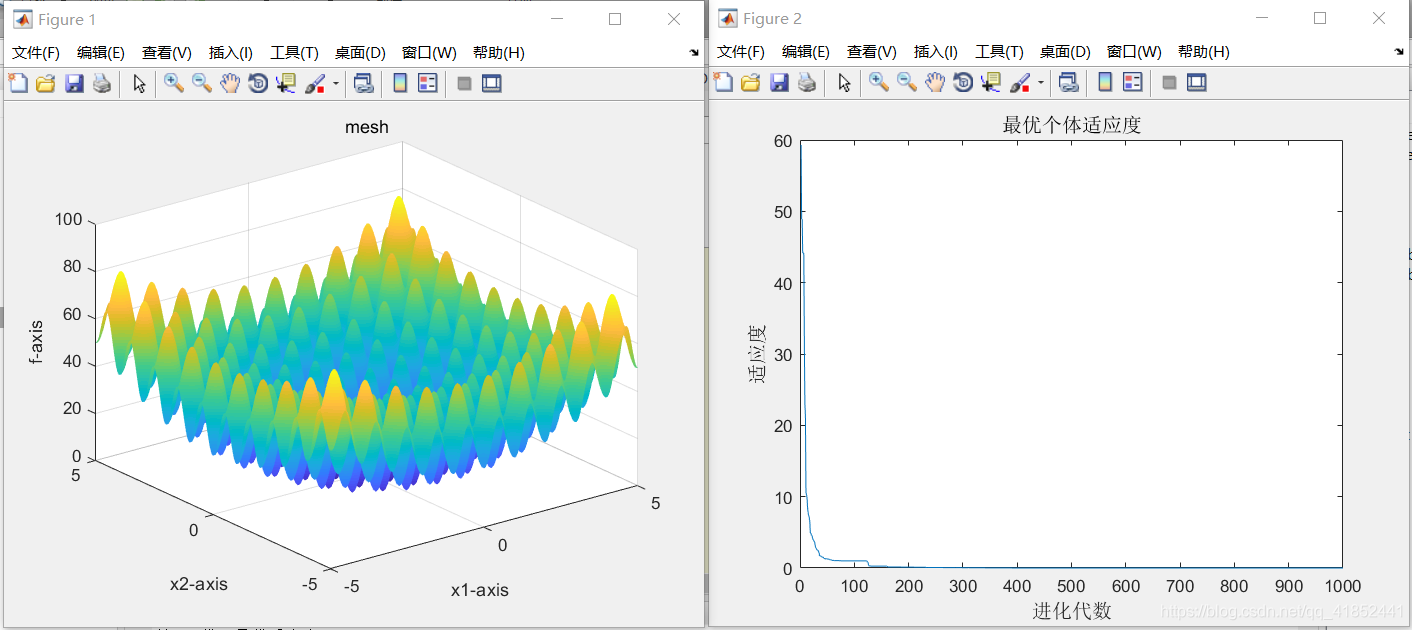
当c1c2越接近，w在0.5左右时，所得的结果越优秀，但若c1=c2，得到的结果却不甚理想。
（2）取c1=1.6，c2=1.4，w=0.5时
检测种群规模和适应度函数维数
①：sizepop=200
dim=8

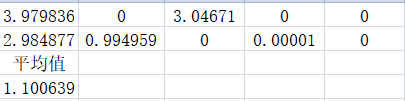
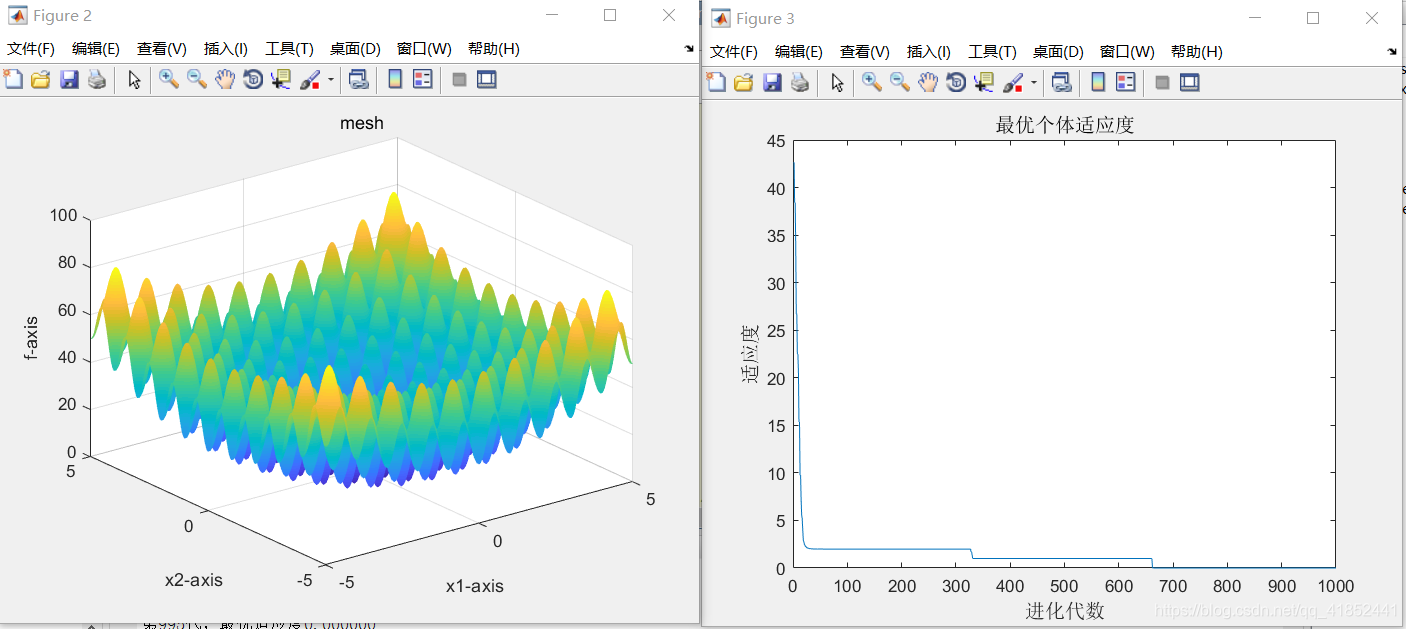
②：sizepop=400
dim=8


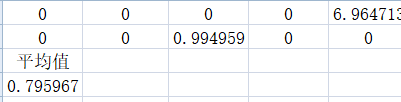
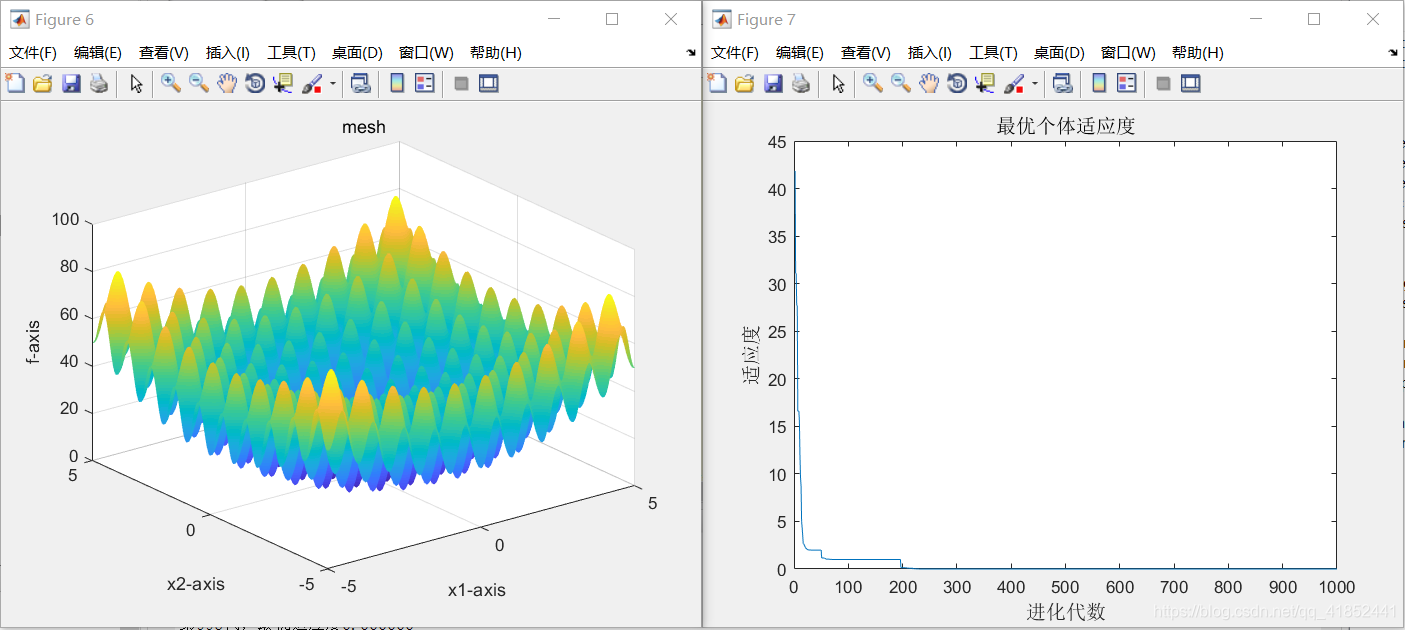
③：sizepop=100
dim=6


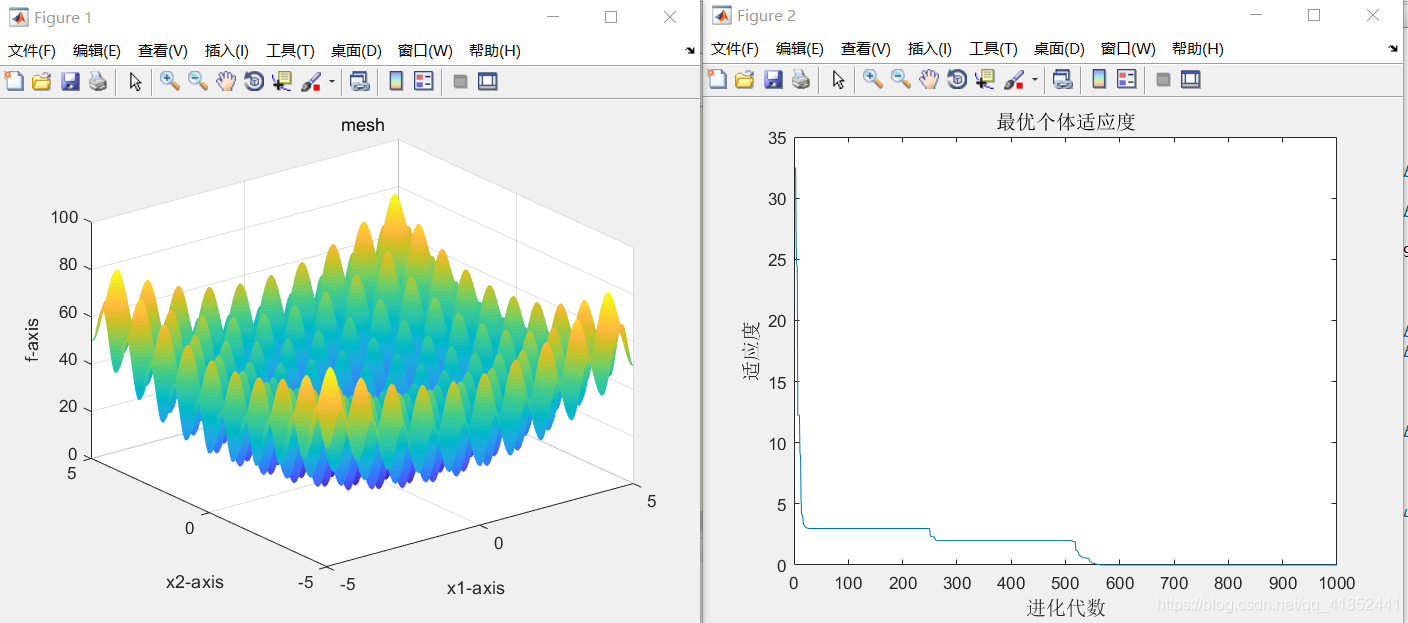
当种群规模越大时，算法运行时间越长，越小则反之，取100-200较为合适
当适应度函数维数逐渐减小时，所的结果越来越优秀，当适应度函数维数为6时已经是最优结果
（3）根据以上结果，取c1=1.6,c2=1.4,w=0.5,sizepop=100,dim=6,迭代次数1000
测试优化函数二和三
①：优化函数Schaffer


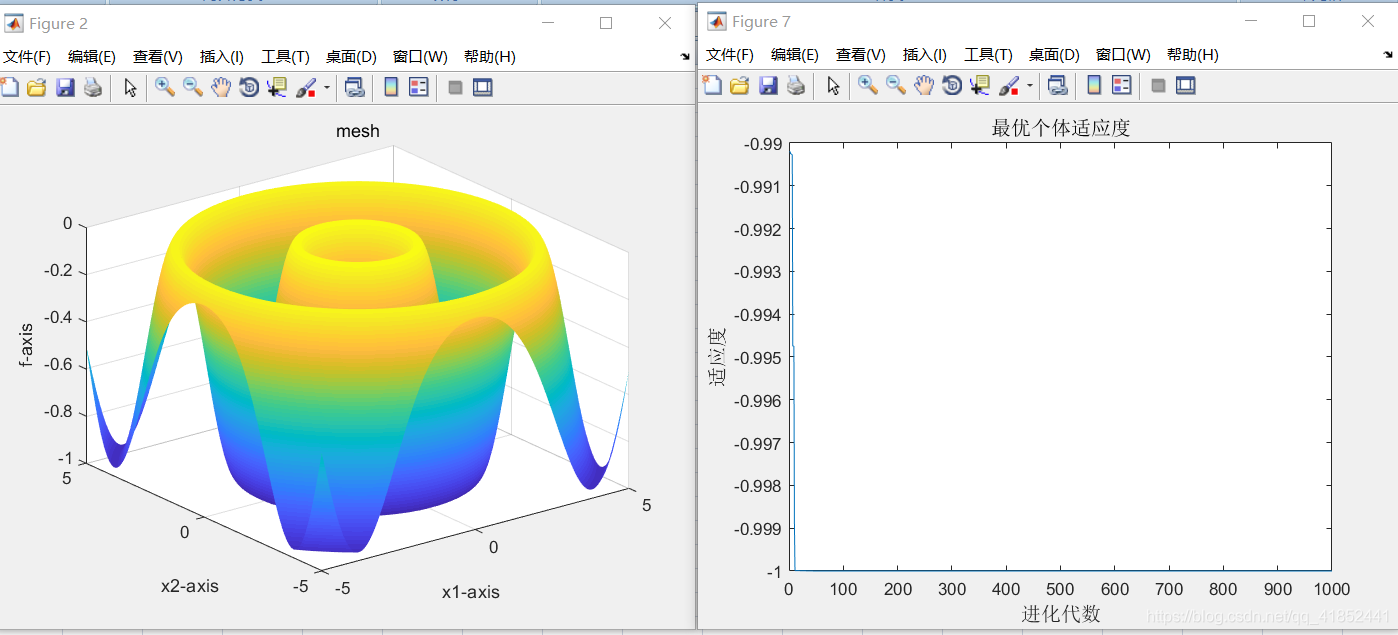
②：优化函数Griewank


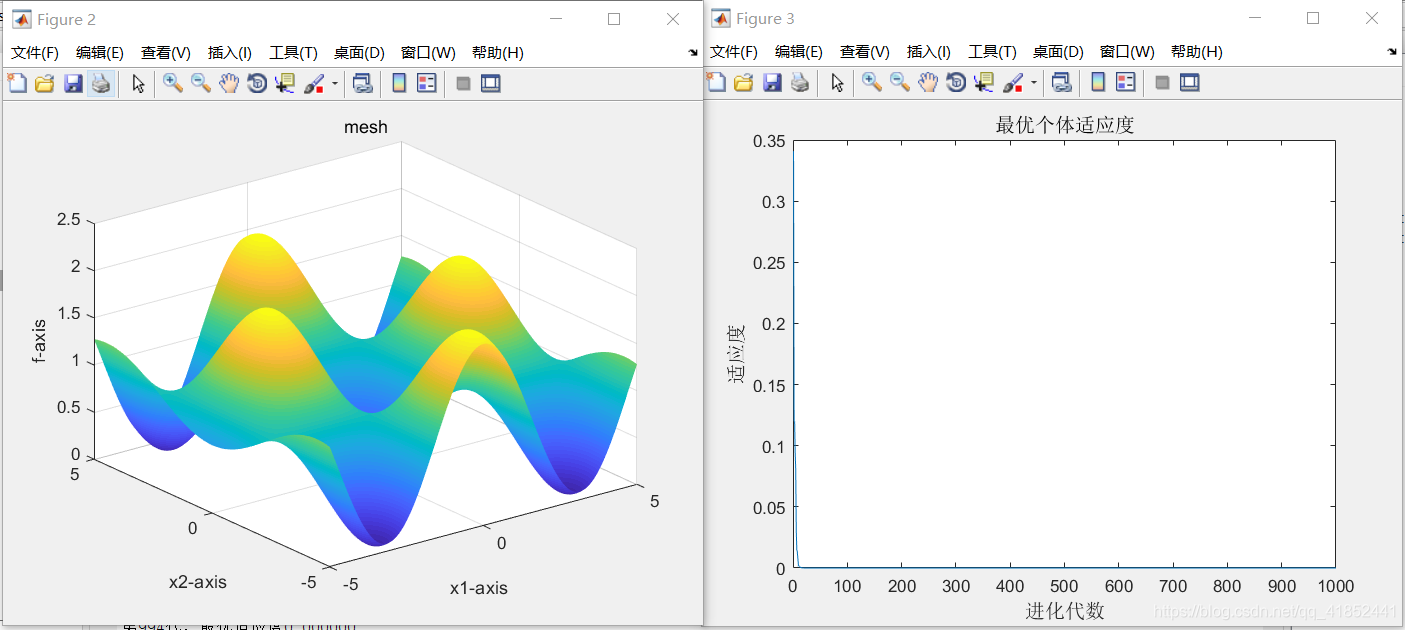
二、结果分析
（1）经测试可得出，加速因子c1c2，代表了粒子向自身极值和全局极值推进的加速权值，两个数据越接近，所得的结果就越优秀，两个数据相差越大，得出的结果便越是不尽人意，但若是两者相等，得出的结果同样较差。
（2）经测试可得出，惯性权重w越大时，得出的结果较为偏离，越小时，得出的结果会越来越优秀，它控制前一速度对后一速度的影响，设置w线性递减对的出优秀的结果有利。
（3）经测试可得出，种群规模sizepop影响算法运行速度，搜索能力与计算能力，当种群规模过大时，算法运行缓慢，所以，sizepop取100-200之间较为合适。
（4）经测试可得出，适应度函数维数dim影响函数复杂性，逐步递减时得出的结果同样逐步优秀，在本次测试中，降低至6时已是最优。

5.实验总结

PSO属于仿生算法，全局优化方法，随机搜索算法，隐含并行性，根据个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等。对高维复杂问题，往往会遇到早熟收敛和收敛 性能差的缺点，无法保证收敛到最优点。
PSO有记忆，好的解的知识所有粒子都保存，算法中的粒子仅仅通过当前搜索到最优点进行共享信息，所以很大程度上这是一种单共享项信息机制。没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。已有利用PSO来进行神经网络训练。研究表明PSO是一种很有潜力的神经网络算法。速度较快且有较好的结果。且没有遗传算法碰到的问题。

参考

百度百科
优快云