本项目详细记录了从需求分析到GUI实现的数独程序开发全过程，包括采用矩阵转换法生成数独终盘、回溯算法解题、面向对象设计、单元测试及性能优化等关键步骤。
首先，附上我的所有代码：https://github.com/mwl0811/sudoku（内含GUI部分的可执行程序和代码）
一、预计的PSP表格
| PSP2.1 | Personal Software Progress Stages | 预估耗时（分钟） | 实际耗时（分钟） |
|---|---|---|---|
| Planning | 计划 | 60 | 90 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 30 |
| Development | 开发 | 60 | 90 |
| · Analysis | · 需求分析（包括学习新技术） | 180 | 150 |
| · Design Spec | · 生成设计文档 | 120 | 90 |
| ·Design Review | · 设计复审（和同事审核设计文档） | 60 | 90 |
| · Coding Standard | · 代码规范（为目前的开发制定合适的规范） | 120 | 90 |
| · Design | · 具体设计 | 180 | 180 |
| · Coding | · 具体编码 | 1200 | 1320 |
| · Code Review | · 代码复审 | 300 | 240 |
| · Test | · 测试（自我测试，修改代码，提交更改） | 300 | 300 |
| Reporting | 报告 | 60 | 60 |
| · Test Report | · 测试报告 | 60 | 60 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| · Postmortem & Process Improvement | · 事后总结，并提出过程改进计划 | 180 | 120 |
| 合计 | 2730 | 2930 |
二、解题思路
- 需求分析：
这一部分主要是分析要求，我总结出了如下的要求：
- 生成不重复的数独终局至文件（0<N<=1000000）
- 生成数独题目（0<N<=1000000）（不在最后程序中体现）
- 读取文件内的数独问题，求解并将结果输出到文件（0<N<=1000000）
- 初期思路：
实现三个功能，就需要分三个模块，但是由于第二点生成数独题目并不是需要在这个程序中，所以对于第二点，我单独写了一个程序。经过我的一番考虑，认为还是用面向对象的方式是比较好的选择，这样还可以保护一些私有变量不被外界改变，类与类之间耦合度降低，满足高内聚低耦合的条件。以下用图的形式简单介绍：
- 查阅资料：
- 生成数独终盘：首先，我查阅了如何生成数独终盘的算法，我原本知道的一个方法是回溯法，但是仔细调研过后，发现回溯法并不是一个很快的算法，在数据量很大时，效率很低，所以我决定采用矩阵转换法，简单而言，就是利用矩阵的行或列的变换，在一个模型的基础上，生成新的数据矩阵，这种算法十分高效，并且充分利用了矩阵的特性，是我看来最好的算法。
- 生成数独题目：然后，对于生成数独的题目，也就是随机挖空，我也研究了很多的算法，这是我看到的一些人的讨论：挖空算法，但是由于这并不是主程序需要解决的问题，所以我就决定选择比较容易实现的算法，也就是随机数挖空，保证了没九宫格挖两个空，再随机挖最多42个空（也许会和之前挖过的某些空重复），这样就实现了不少于30个，不多于42个空的数独题目。
- 解数独题目：最后，要解决的的就是解数独题目的算法，在我本来就知道的范围内，我知道的算法依然是回溯法，我也上网查阅了很多资料，虽然说也有稍好一点的算法，但是由于没有具体的解释，所以我最后决定还是采用回溯法，用dfs（深度优先搜索）来解决这个问题。
三、设计实现及代码说明
由于考虑到后续需要单元测试的过程，我把我的代码分成了三个模块，分别是Check.h，Generator.h，Solver.h，还有一个单独的生成数独题的代码question.cpp,它们的功能如下：
- Check.h：主要负责输入的命令部分，对于许多命令输入错误的情况，给出错误的提示，这个部分十分简单，下面是代码部分，有注释解析：
int checkinput()
{
if (argc != 3) //输入格式不正确
{
cout << "Illegal paramater number" << endl;
cout << "Input like this: [sudoku.exe -c n] or [sudoku.exe -s path]" << endl;
return 1;
}
if (!(compare(argv[1], "-c") || compare(argv[1], "-s"))) //字母错误
{
cout << "The first parameter should only be -c or -s" << endl;
cout << "-c means to generate the sudoku to file." << endl;
cout << "-s means to solve the sudoku from the file." << endl;
return 2;
}
if (compare(argv[1], "-c")) //创造数独终盘
{
int sum = 0; //sudoku的个数
size_t len = strlen(argv[2]);
for (int i = 0; i < len; i++)
{
if (!(argv[2][i] >= '0' && argv[2][i] <= '9')) //输入的字符不合法（不是数字）
{
cout << "The third paramater after -c should be number that indicate the sudoku you want." << endl;
if (argv[2][i] == '+' || argv[2][i] == '-' || argv[2][i] == '/' || argv[2][i] == '*')
{
cout << "Please input the number!" << endl;
return 8;
}
return 3;
}
sum = 10 * sum + argv[2][i] - '0';
}
if (sum > MAX || sum < 1) //数字过大
{
cout << "The number is too large,the number should be 1-1000000" << endl;
return 4;
}
FILE* file;
file = freopen("sudoku.txt", "w", stdout); //没有文件时可以创造
Generator generator(sum, file); //调用Generator
generator.generate();
return 5;
}
if (compare(argv[1], "-s")) //解题
{
FILE* ans;
FILE* question; //数独题目
question = freopen(argv[2], "r", stdin);
if (!question)
{
cout << "The file path is not right,please check." << endl;
return 6;
}
ans = freopen("sudoku.txt", "w", stdout);
Solver solver(question, ans); //调用Solver
flag = solver.in();
return 7;
}
}
注：返回的数字是便于后续的单元测试
- Generator.h:主要负责生成数独局的终盘，采用的是矩阵转换法，我的思路流程如下：
整体部分：
矩阵变换部分：
接下来是部分重要的代码：
void generate() //生成函数
{
int number = 0;
while (number < count)
{
Out();
number++;
Line_exchange_floor(&number);
Line_exchange_middle(&number);
Line_exchange_ground(&number); //换行
if (number < count)
{
TransForm();
Change();
}
}
}
注：上面的代码是生成矩阵的函数generate
- Solver.h是用来解决数独题的部分，采用回溯算法，由于回溯法是比较普遍的算法，所以在这里就不过多介绍了，附上我的代码（主要是dfs部分）：
bool dfs(int tot) //dfs搜索方法
{
if (tot > 80)
{
return true;
}
int line = tot / 9;
int col = tot % 9;
if (sudoku[line][col] > 0)
{
return dfs(tot + 1);
}
for(int i = 1;i <= 9;i++)
{
sudoku[line][col] = i;
if (check(line, col, i))
{
if (dfs(tot + 1))
{
return true;
}
}
sudoku[line][col] = 0;
}
return false;
}
- question.cpp是用来生成数独题目的，要求如下：
9乘9的棋盘上，挖空不少于30个，不多于60个，每个3乘3的的小棋盘中，挖空不少于2个。
所以我的算法是这样的：在每个3乘3的小棋盘中先每个随机挖空2个，这样就已经有了18个空，接下来我再随机挖空42个（这42个空有与已经挖好的空重复的可能），那么此时就能满足条件。随机算法如下：（这里用到了rand函数）
void change()
{
int a = 0, b = 2;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
for (int k = 0; k < 2; k++)
{
int ran1 = (rand() % (b - a + 1)) + a;
int ran2 = (rand() % (b - a + 1)) + a;
if ((ran1 + i * 3)*(ran2 + j * 3) != 0)
{
incom_sudoku[ran1 + i * 3][ran2 + j * 3] = 0;
}
}
}
}
a = 0, b = 8;
for (int i = 0; i < 42; i++)
{
int ran1 = (rand() % (b - a + 1)) + a;
int ran2 = (rand() % (b - a + 1)) + a;
if (ran1*ran2 != 0)
{
incom_sudoku[ran1][ran2] = 0;
}
}
}
四、单元测试及代码说明
单元测试的部分我一共写了十个用例，因为对于输入错误的情况有很多，所以测试的输入也要有很多，我一共设计了八个关于输入的测试（也就是对Check.h的测试），然后剩下的两个测试分别是对生成数独终盘（Generator.h）和求解数独（Solver.h）的测试。
由于对于输入的测试比较简单，所以在这里我只介绍对于Generator.h和Solver.h的测试。
- Generator.h的测试：
方法：检查生成的矩阵是否有重复的情况
TEST_METHOD(TestMethod10) //证明Generator没有生成重复的矩阵
{
int sudoku_number = 1000000;
FILE* file;
freopen_s(&file, "sudoku_temp.txt", "w", stdout);
assert(file != NULL);
Generator sudoku_generator(sudoku_number, file);
sudoku_generator.generate();
fclose(stdout);
freopen_s(&file, "sudoku_temp.txt", "r", stdin);
assert(file != NULL);
string s1;
bool end = false;
set<string> container;
while (true)
{
int temp;
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
if (fscanf_s(file, "%d", &temp) == EOF)
{
end = true;
break;
}
s1.push_back(temp + '0');
}
if (end) break;
}
if (end) break;
container.insert(s1);
s1.clear();
}
fclose(stdin);
assert(container.size() != sudoku_number);
}
- Solver.h的测试：
方法：主要是检查生成的数独矩阵是否正确。
TEST_METHOD(TestMethod9) //测试solver生成的矩阵是否正确
{
argc = 3;
argv = new char*[3];
argv[0] = new char[100];
strcpy_s(argv[0], 100, "sudoku.exe");
argv[1] = new char[100];
strcpy_s(argv[1], 100, "-s");
argv[2] = new char[100];
strcpy_s(argv[2], 100, "solver.txt");
Check check7(argc, argv);
assert(check7.flag == 0);
}
注：flag是对于矩阵的检查标志，一旦有某个矩阵出现错误，flag就被置成1，有一个valid函数在Solver.h的内部，用于检查是否有错。
下面是我单元测试的结果，证明我检查的部分都正确了：
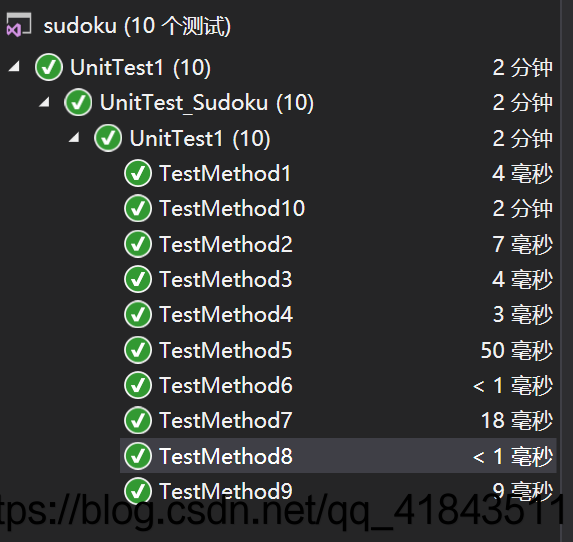
注：方法10的测试比较慢，主要是因为我输入了1000000个矩阵进行测试，证明在最多输入时，也可以得出不重复矩阵，这样可以使得测试更具有说服性。
- 覆盖率展示：
可以看出，测试代码的覆盖还是比较好的。
五、程序性能及质量分析
起初，我选择的生成方法是回溯法，代码是很慢的，生成1000000个数独终盘要花40s的时间，所以我换了矩阵转换的算法，节省了大量的时间，效率非常高，性能上也提高了很多，并且我还删除了一些不必要的循环，最后的算法生成1000000个数独终盘只用了不到4s的时间，性能提高了十倍。下面是我的性能分析：
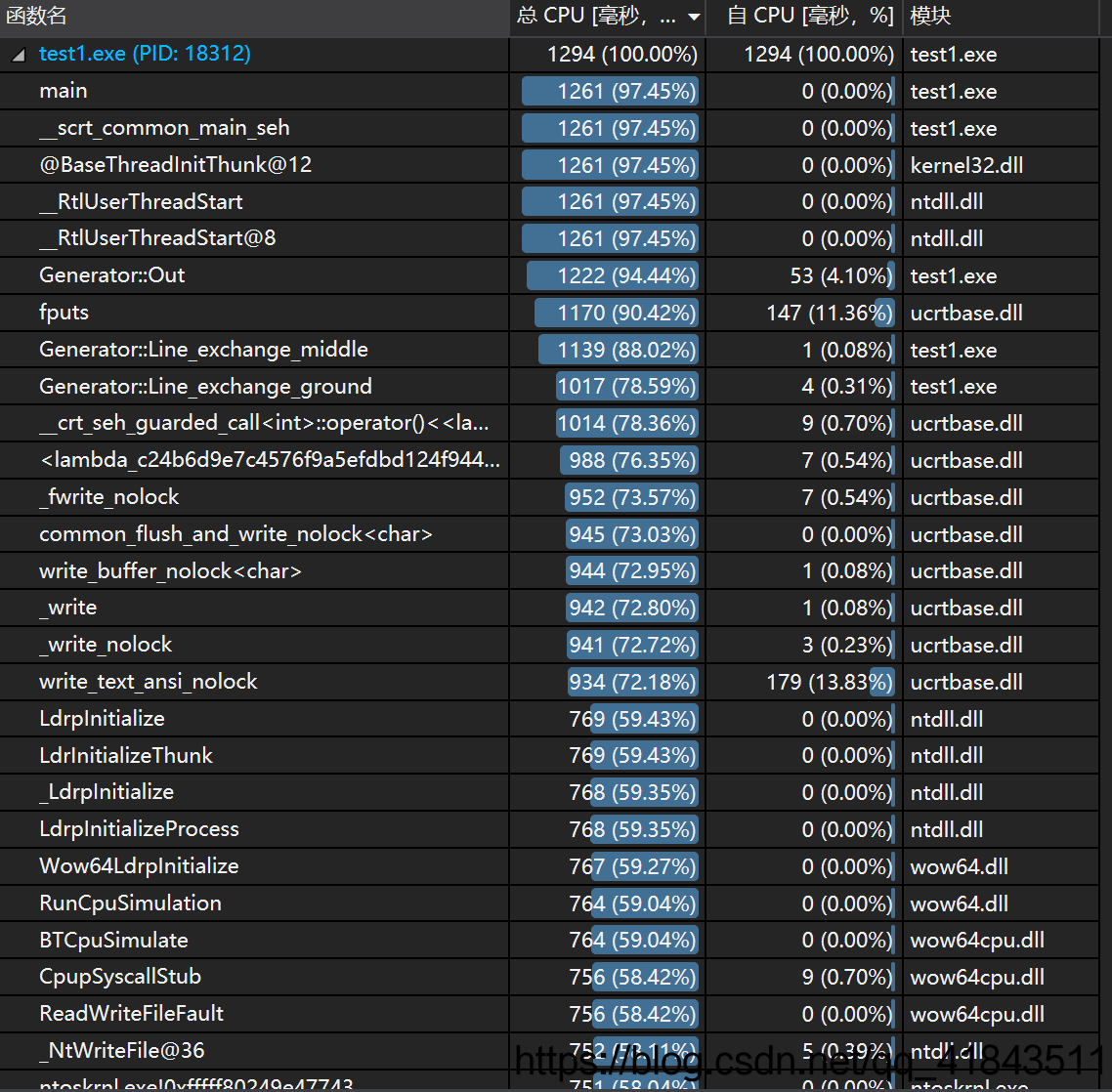
注：我为了便于性能分析，就把原文头文件中的内容全部合成了在一个cpp文件中，文件的名称是test1。
这里可以看到，比较费时间的是Generator类中的out()函数，也就是输出函数，但是这一部分是不可避免的，没有办法再做更好的提升。
为了提高程序的质量，我消除了运行过程中提示的警告，过程如下：
可以看出这里对checkinput某些情况没有返回值，但实际上，根据代码来看，所有的情况都已经讨论完全了，不存在没有返回值的情况，但是为了提高质量，我在这里加了一个返回值，如下：
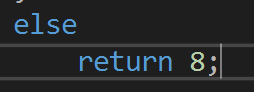
然后再次运行，可以看出，已经没有警告出现：
六、GUI
对于GUI的设计，之前一直听说用QT写比较简单，所以这次就想借这次机会尝试一下，代码部分还是比较容易实现的，生成数独终盘和数独局都是已经写好的代码，在接口中调用即可，然后检查数独正确与否的代码，也是在单元测试中就用到过的回溯法代码，所以，在这个环节中，要实现的就是接口功能。
- 我的思路：我的程序执行方式是，在起初输入想要生成题目的数量，然后调用Generator.h生成对应数量的数独终盘，然后利用question的代码按照要求随机挖空，展示出数独局，最后用valid函数对结果进行正确性判断。
int checkedsd[9][9];
for(int i=0;i<9;i++)
{
for (int j = 0; j < 9; j++)
{
QString s = this->le[i][j].text();
checkedsd[i][j] = s.toInt();
}
}
if (valid(checkedsd) == true)
{
QMessageBox::about(this, tr("提示信息"), tr("You Got it!"));//成功解出
}
else QMessageBox::about(this, tr("提示信息"), tr("Wrong Answer!"));//弹窗提示错误
注：这一段代码是对输入结果的测试，对于正确还是错误给出对应的提示。
以下是程序执行结果的展示：
注：这是数独题目生成的结果。
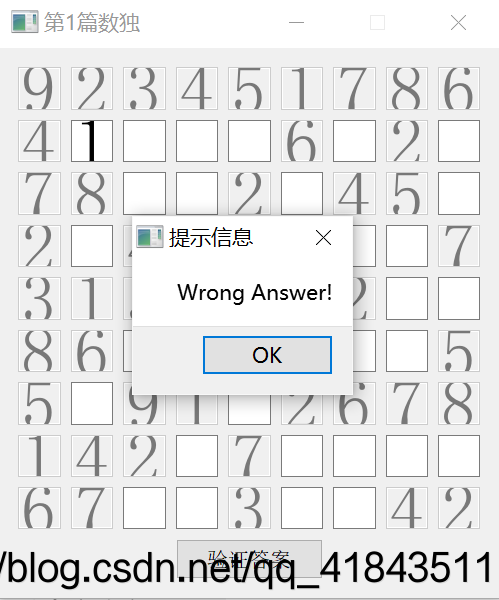
注：这是数独题目填写错误的结果。
注：这是数独题目填写正确的结果。
由于这一部分是用QT编写的，没有连接到GitHub，所以只提交了一次最终结果。
七、总结
这一次的项目，我学到了很多，有很大的收获，下面是我通过这次经历学到的：
- 知道了设计一个程序的前期工作
- 知道了很多代码可以改进的方向和方法
- 明确了代码规范的重要性
- 学会了如何进行单元测试
- 学会了如何使用github管理我的程序代码
- 学会了如何用QT编写GUI
- 学会了如何用优快云撰写博客
扫一扫
837
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
