参考
最近在实现程序化天空盒,到了实现大气散射这一步,索性查漏补缺,把大气散射这块儿的理论知识补充明白了。跟着【实战】从零实现一套完整单次大气散射_一的推荐,学习这块我直接从Volumetric Atmospheric Scattering啃起。
补充一点!本篇文章实际上是作为一个阅读笔记来写的,因此条条框框并没有写的很清晰~以下的图均来自Volumetric Atmospheric Scattering。
同时部分内容还参考了乐乐女神的: [Rendering] 基于物理的大气渲染
1 引入
材质外观会由光是否能穿透材质决定——半透明物体的渲染结果来自于内部结构与光线相互作用的结果。但如果我们想实现玉石这种半透明物体已经有对应的方法了,例如Fast Subsurface Scattering in Unity中展示的方法渲染出的玉石:

但很遗憾,这种通过Ray Tracing仅模拟出表面材质的效果,是难以渲染出一个真实天空的样子的。除了渲染出“outer shell”,还需要考虑大气效应(atmospheric effects)——模拟出光线穿透大气会发生什么(大气散射),那就需要上体积渲染了!体积渲染(Volumetric Rendering)是计算光在物体内传播的渲染方法,而体积渲染常用的Ray Marching和SDF(Signed Distance Functions)用来模拟大气散射也不是很高效(本人没实操过,是参考的文章里的话~),一种更好的模拟固体半透明物体的方法——体积单散射(Volumetric Single Scattering)就被顺利的提出!
1.1 光在介质中传播
为了节约性能实现高效计算,大部分的游戏引擎(Unity&UE)都假设光在真空中传播,这就意味着物体们就成了唯一能影响光线传播的因素。但现实中光是通过介质传播的!这样我们看到的物体的外观就会收到光线穿透程度的影响。地球表层空气密度低,这样稀薄的大气层导致光线需要传播很远我们才能看到,所以很远很远的山脉看上去就像跟天空连为一体,但靠近我们的物体是不会被大气散射所影响的。
复刻大气散射第一步——了解光如何在介质(例如空气)中传播的。由于光线只有进入人眼才能被人眼到看到,因此在图形学学习过程中往往会把人眼比作rendering的相机。而空气中的分子(介质中的粒子)是可以使穿过它们的光线发生偏转的,那么以人眼(相机)是否看得见偏转后的粒子为划分依据,可以把这些粒子影响观察的过程分为外散射(Out-Scattering)和内散射(In-Scattering)。
1.2 外散射 Out-Scattering
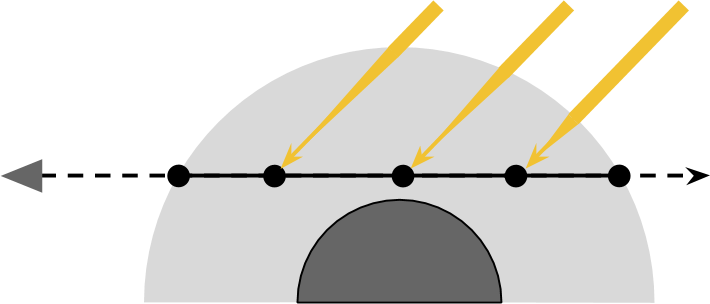
一束射向相机的光线打在了介质粒子上发生偏转,这就是外散射。
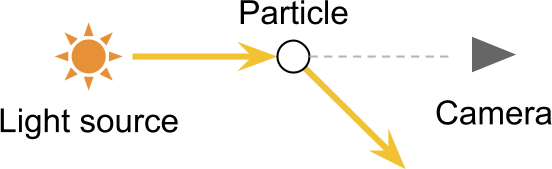
介质密度&传播距离
以上只是一束光线的效果,但真正的光源每秒会发射亿万光子,每个光子都有几率击中介质中的粒子,介质密度越大,光子击中且发生偏转的概率也就越大。

上图体现了一个衰减的过程:向外散射导致光逐渐变暗,传播距离越远越暗。这个变暗的程度是由传播距离和介质密度共同决定的。
1.3 内散射 In-Scattering
有了外散射做参考,内散射就更好理解了:一束本身不是射向相机(其他方向)的光线打在介质粒子上发生偏转后恰好到了朝向相机的方向上,这就是内散射。
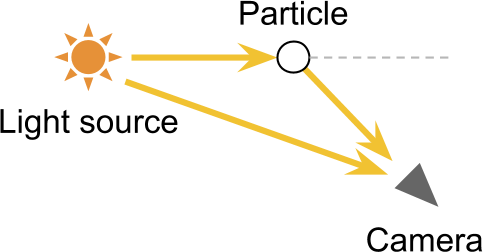
相机会同时接收来自同一个光源的直接和间接光线,放大了收到的光子数量,光源周围的光晕(light halos around light sources)就是这么个道理。
2 单次散射过程
上面提到了光线是如何在介质中传播的,这里我们需要进一步知道光线穿过一个行星的大气层时发生了什么。首先定义一点:接下来说的单次散射仅考虑光线从太阳发出只经过一次散射改变方向后射入相机(人眼),即只考虑沿视线发出的内散射:

当然,肯定有很多其他的传播方式,但就如文章Part1末尾的cheat sheet所述,考虑可能的散射路径越多,计算所需的散射次数将呈指数增长。
2.1 PtoA发生的外散射
首先考虑外散射,那么就要有上面提及的衰减问题,AB上的每个点P都会有几率偏转,如下图所示:
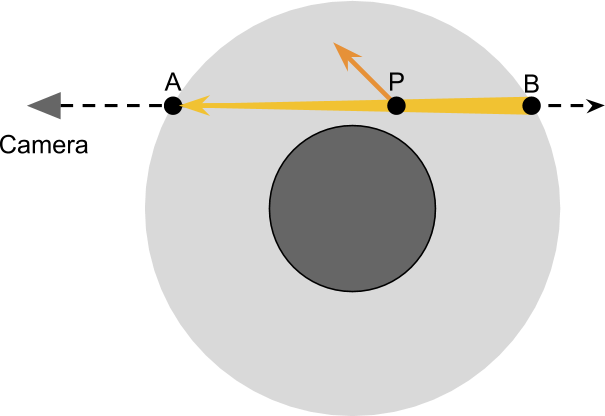
2.2 PtoA发生的内散射
想要计算P点发生的外散射,首先我们需要知道P点到底有多少光:假设只有一个恒星照亮当前这个行星,那就是太阳,这样的话P点的光都来自于太阳了,这些光一部分来自于内散射:
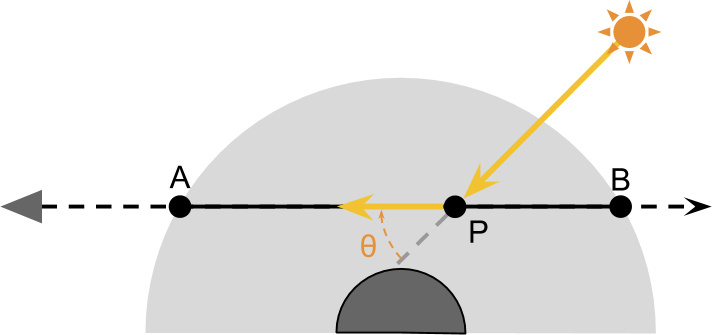
Sun --> P --> Camera这两步骤就足以近似计算模拟出大部分大气效应了。
2.3 SuntoP发生的外散射
但!如果考虑考虑Sun --> P的过程中光线的外散射,things are getting more complicated...如下图,对于AB中的每个点Pi都需要考虑
- Sun --> Pi过程中发生的外散射
- Pi --> Camera过程中发生的外散射
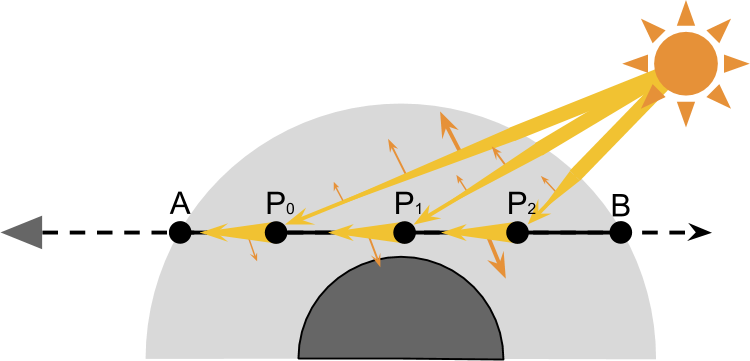
3 理论
3.1 衰减系数T
其实已经来到了这个tutorial的Part2:The Theory Behind Atmospheric Scattering - Alan Zucconi
为了计算肯定要用各种数学参数去模拟上述的这样一个过程,我们从Sun --> P开始,将过程细化成下图,光从太阳出发直到与大气层边缘相交的C点过程中不发生散射,我们定C点的光照强度为,C进入大气层 --> P过程中发生散射,一路经过衰减后到达P点的光照强度为
:
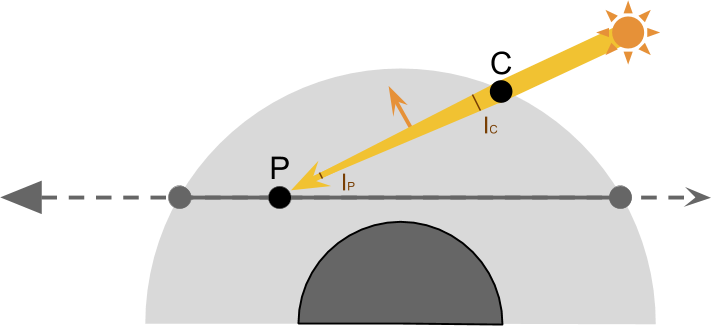
我们将与
比值叫做衰减系数(Transmittance),用以表示某段光线传播路径上光照的衰减程度(没有被散射的光照占比),那么P点接受的光照可以被表示为:
3.2 散射系数S
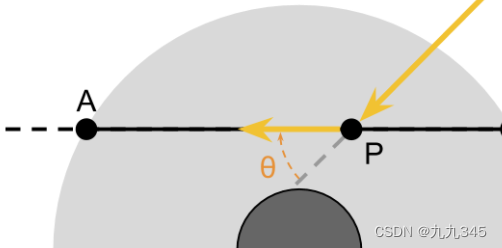
P点的光强知道之后,接下来就是计算P点发生散射后沿着路径PA到达相机的光照,这里我们先引入一个参数,散射系数(Scattering)
用以表示这次散射有多少光被反射到了方向上,
是P点的高度,
是波长。
那么有了散射系数S项+衰减系数T项,我们就能表示P to A的光照强度:
依据此就可以总结出以下4点,我直接截图了文章的总结部分,为了方便后续的回顾~

3.3 对AB每一点进行积分
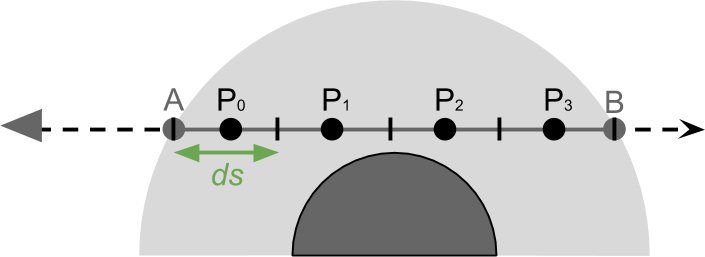
上面一直都是针对AB上的其中一个P,但实际上计算我们需要把每个P点的贡献都考虑进去。A点接收的光强为,理论上讲想要遍历AB上的所有点
是不可能的(AB上有无数个点),想要计算
该怎么做呢?——积分!把AB划分成无数个ds,计算每个ds合起来的结果:
实际上就是求个积分,
两点需要解释的,
- ds越小,取的点就越多,结果也就越精确
- 在后续的shader中会采取遍历
,叠加结果的方式进行计算
将太阳光考虑成平行光
,对于行星大气效应计算来说,我们可以假设太阳光考虑成平行光,那么下图的每个P点对应的C点接收相同强度、相同方向的光。
那么对上述公式可以进行简化:
其中,用替代了
,表示太阳光强度,这样的话其实
也是定值,后面会继续对这个式子进行进一步拓展。
4 Rayleigh散射
由于大气层并不是均匀介质,密度和构成会随着海拔的变化而变化,那就不可能得到一个适合所有情况的计算模型,因此需要针对特定情况提出适合的模型。大多数的行星大气光学效应可以通过Rayleigh散射(Rayleigh Scattering)和Mie散射(Mie Scattering)这两种模型来计算实现。
- Rayleigh散射模拟构成大气层的大部分小分子(氧气、氮气)如何反射光线,我们所看到的天空的颜色(白天的蓝色、日落时的红色)就是由Rayleigh散射决定的
- Mie散射模拟低层大气中悬浮的大分子(花粉、灰尘)如何反射光线,天空中云朵的白色就是由Mie散射决定的
4.1 计算光线占比
光与小分子发生碰撞后,一部分光穿过粒子继续向前;一部分会反弹回来;小部分会向各个方向发散,当然拐弯90°的占比肯定是最小的。下图展示了Rayleigh散射光的分布:
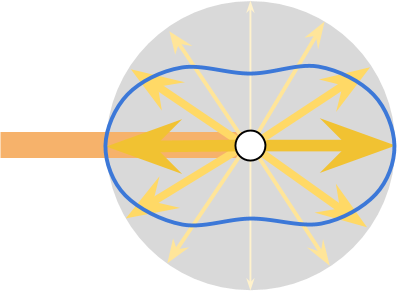
提到某一特定方向上的散射光占比,就能想到我们的散射系数S项:
其中 表示光线与分子碰撞前.紧接着S项可以细化为:
其中, 是入射光波长;
是散射角;
是当前碰撞点的海拔;
是空气折射率,一般取1.00029;
是标准大气密度,一般取
;
是高度为
处的相对大气密度(海平面处为1,随着h的增加不断减少),可以理解成h处真正大气密度/海平面大气密度,一般会使用指数函数进行拟合计算:
其中,H=8500m,是大气厚度
分析
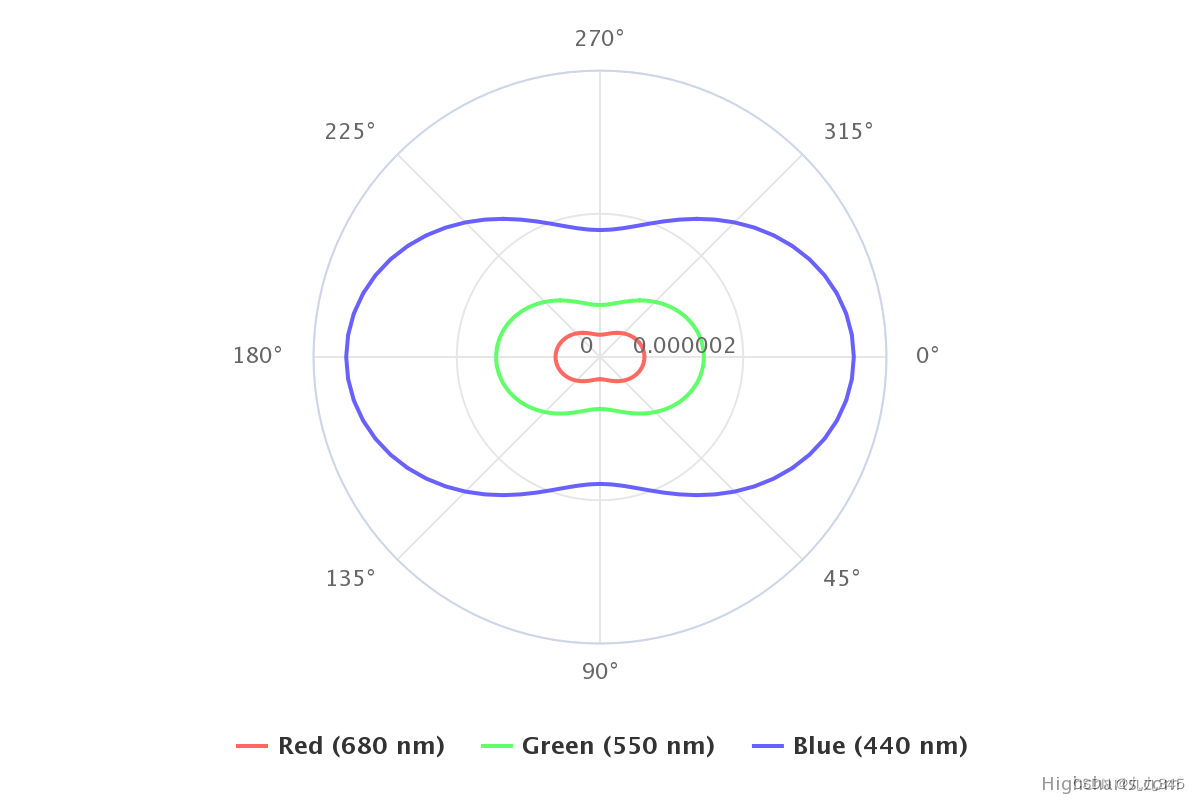
从上面的公式可以看出,首先,某些方向接收的光比其他方向多得多。其次,波长影响占比还挺大的(散射系数和波长的4次幂成反比),波长越短意味着被散射的越厉害,例如原文列举了三种波长的结果(如下图,其中S=0代表着海平面的散射),红 --> 绿 --> 蓝依次波长变小,散射系数变大。
这也正说明了:
- 为什么白天天空是蓝色——蓝光在大气里不断被散射
- 为什么日落的时天空是红色——阳光要穿透更厚的大气层到达人眼,蓝光都被散射出去了,留下了红光
4.2 计算能量占比
计算完被反射到某一特定角度上的光线占比,接下来就是计算经过散射后入射方向上还剩多少光。我们假设经过一次散射损失了占比为的能量,它也被叫做Rayleigh散射系数:
海平面Rayleigh散射系数
上面提到过对上所有的P积分,如果每个ds都要计算一次
,计算量将会非常大!为了节省计算成本,往往会提取出数值不会变的部分-->h=0时的海平面Rayleigh散射系数:
其中,h=0.
分析
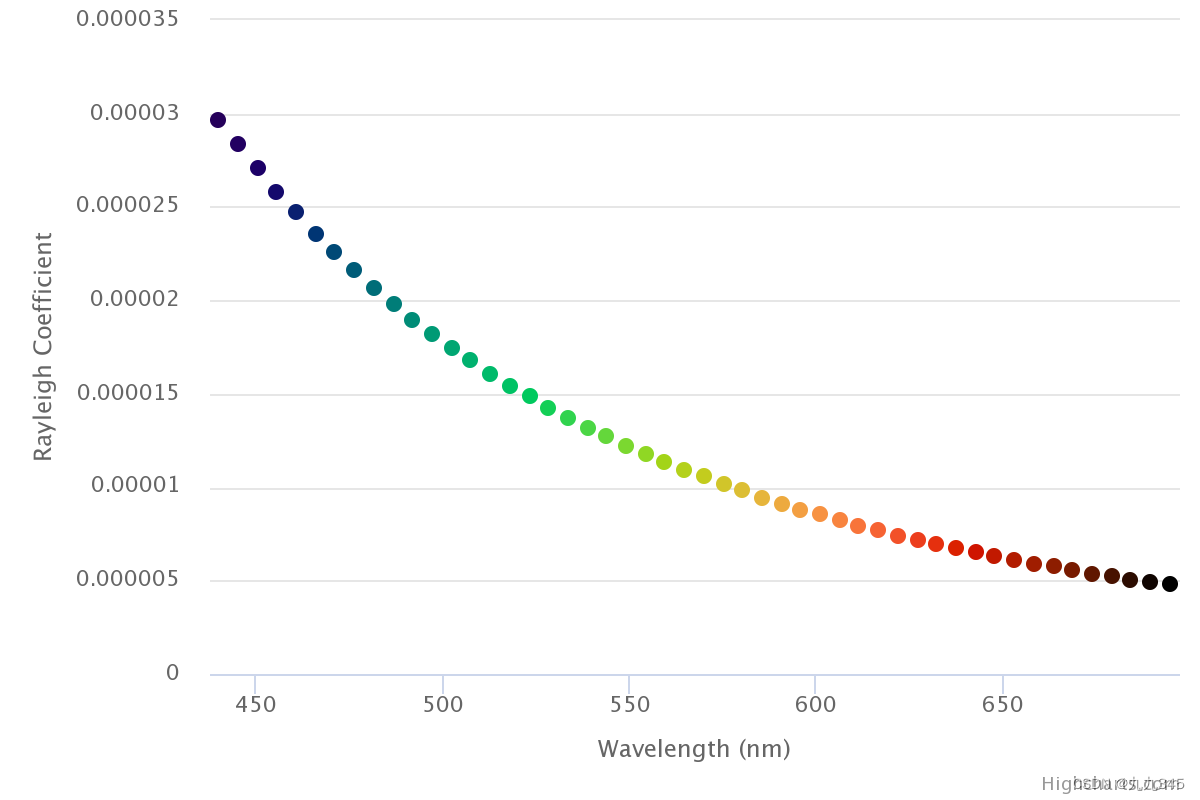
下图是不同颜色(波长)和Rayleigh散射系数的关系图,也是通过和
这样的关系我们才知道:光线最初从太阳发出到达大气层时波长分布是很广的,进入大气层后跟大气层中的小分子碰撞发生Rayleigh散射,与波长更长的红光相比,蓝光更容易被散射。
这也能从另一个角度说明了:
- 为什么白天天空是蓝色——光一到达大气层,蓝光就向各个方向散射出来了
- 为什么日落时天空是红色——日落时分,太阳光穿过大气层几乎平行于海平面传播,拥有很长一段传播光程,在这个过程中蓝光已经被散射的差不多了,到人眼中就只剩下红光啦!
4.3 Rayleigh相位函数
我们的散射系数S项可以被分为两个部分:
- Rayleigh散射系数项
——描述散射强度,就是4.2介绍的
- 散射几何项
——用以描述其方向性,表示被散射的能量中有多少比例被反射到了
方向上,又被叫做Rayleigh散射的相位函数
其中相位函数的推导过程其实很简单,我直接截图原文:

回顾
第4节我们涉及到了:
散射系数
Rayleigh散射系数
海平面的散射系数
Rayleigh散射相位函数
5 相对大气密度
我们进入了第四部分A Journey Through the Atmosphere的学习,探讨了的作用。
5.1 指数衰减关系
理论来讲,密度越大的大气层,发生散射的几率越大。由于大气密度会随着高度急剧降低(对流层的温度和大气压会骤降),Rayleigh散射大部分发生在海拔0-60km的低层大气。
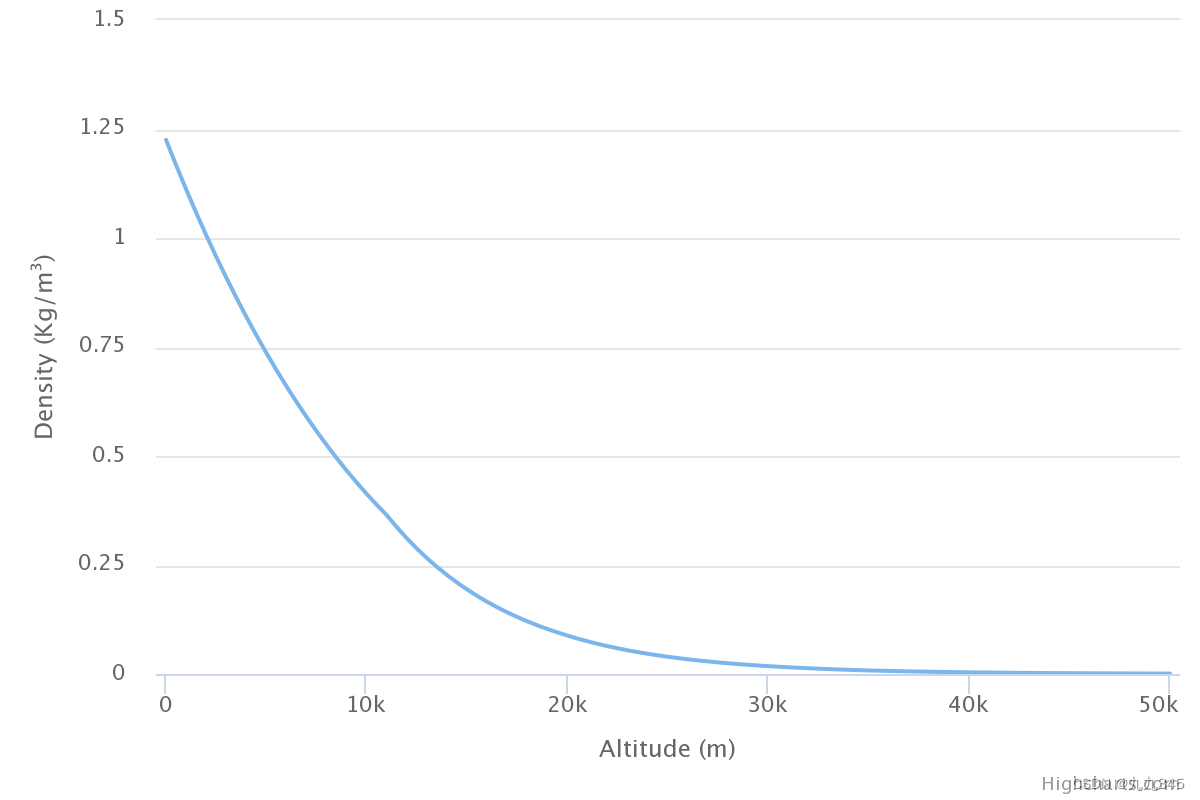
上图是密度与海拔之间的关系,几乎呈指数衰减的关系,而之前说了,
而海平面(h=0)的密度为1,那可以近似将低层大气的相对密度视为指数关系,也就是上文已经介绍过的:

5.2 大气厚度H
Rayleigh散射H一般取8500m,Mie散射一般取1200m左右。
6 再谈衰减系数
我想有必要再唤起之前3.1中提到的衰减系数(原谅我直接粘贴3.1写的内容,省的翻了嘿嘿~):
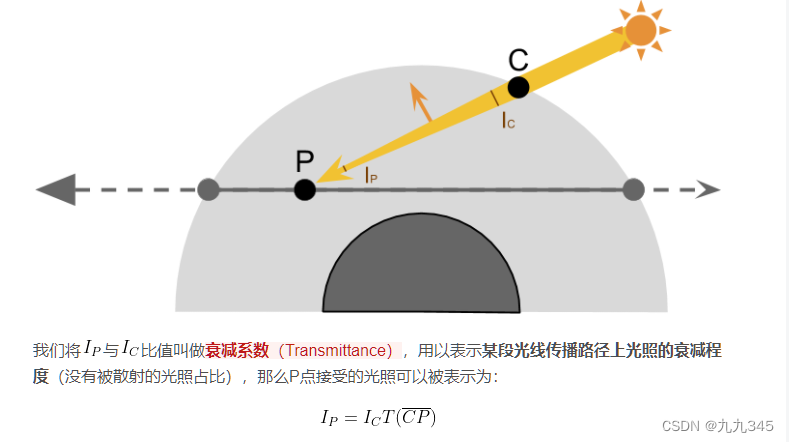
啊!我们好像搞清楚了这个衰减到底是怎么一回事了——指数衰减;每次散射衰减出去的量我们也知道了——,那接下来要做的岂不就是补充完整上面计算
的公式了吗!
开动。
6.1 单一碰撞的衰减
暂且不把散射发生仅仅局限在点C和点P,我们另外定两个参数,原始光照强度和经过外散射能量衰减之后剩下的光强
,我们就能得到适用于单一碰撞的能量衰减公式:
6.2 一段距离x的衰减
参考[Rendering] 基于物理的大气渲染中将简单和复杂情况分开讨论:
简单情况
这里就需要用到微分了,如果我们认为是个定值的话,那么衰减一段距离x后的剩余能量
就是:
具体推导可以看看原文的这个cheat sheet:

复杂情况
这里的复杂就是指会随着
和
变化而变化,就不是定值了,就需要原原本本写成积分的形式:
这也正是符合实际计算的情况。
6.3 计算衰减系数T
还记得在第2节中一共有SuntoP和PtoA两种情况的外散射,二者都需要考虑能量的衰减,都需要考虑衰减系数T。AlanZucconi的文章是从CtpP的角度计算的,也就是,而乐乐女神的文章是从PtoA的角度计算的,也就是
。
两个角度都没什么问题,推导过程就不放上来了,直接截图给上结果(公式太多了不想再打一遍hhhh):
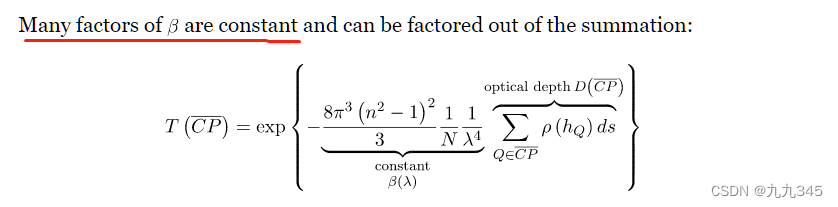
同样这里首先给定了是定值的前提,你会发现这个公式可以被简化写成:
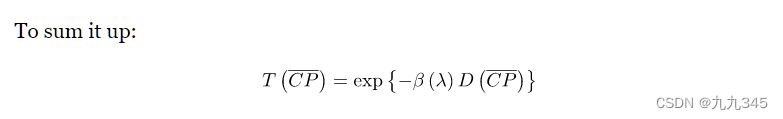
其中,是海平面的Rayleigh散射系数;后者是光学距离(Optical Depth)。
光学距离
对比6.2中简单情况路径取x,这里是更宽泛的CtoP,这部分的积分可以理解为光学距离,也是后续shader中实际需要进行计算的部分,
分析
从上述公式可以看出,
- 随着高度增加,相对大气密度降低,相对密度Rayleigh散射系数不断减小
- 海平面的Rayleigh散射系数只跟波长相关,甚至不需要在传播路径上进行积分!
7 计算PtoA光照贡献最终项
第2节中已经探讨过PtoA有内散射+外散射;6.3中我们给出了A衰减系数T项的计算公式;4.3的最后我们把散射系数S项页拆分成了两项。
那么我们最终的计算就可以按照下述步骤逐步精简(图来自乐乐女神那篇文章的推导过程截图~):

到这里,就完成了单次散射数学模型的推导过程啦!接下来会继续进行整个shader部分的学习,建立大气渲染模型。





 本文深入探讨了大气散射的理论基础,包括光在介质中的传播、外散射与内散射、单次散射过程,以及Rayleigh散射模型。通过解析光的衰减系数、散射系数和相对大气密度等关键概念,阐述了如何模拟大气效果。此外,还介绍了如何计算PtoA光照贡献,为实现程序化天空盒提供了理论支持。
本文深入探讨了大气散射的理论基础,包括光在介质中的传播、外散射与内散射、单次散射过程,以及Rayleigh散射模型。通过解析光的衰减系数、散射系数和相对大气密度等关键概念,阐述了如何模拟大气效果。此外,还介绍了如何计算PtoA光照贡献,为实现程序化天空盒提供了理论支持。

















 337
337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










