菜鸡奋斗路03-树3 Tree Traversals Again

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

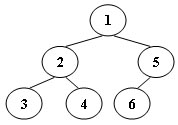
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N$ ($\le 30$) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to $N$). Then $2N$ lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

作者: 陈越

单位: 浙江大学

时间限制: 400ms

内存限制: 64MB

代码长度限制: 16KB

---

个人分析：？？怎么又要遍历树了，emmmmmm。题目给出了目标树中序堆栈遍历的出入栈顺序，要求据此得出目标树的后序遍历顺序并输出，输出老套路，前面各个数都要用空格隔开，最后不能有空格。菜鸡第一想法：根据输入建树，然后写一个后序遍历输出即可。

又是一句这么简单的分析.....现在看越清晰的题目越害怕，弯弯绕不一定就少。

“根据输入建树”这就是第一个弯了，一般来说，可以根据树的前中后序遍历中的二者，求出第三者。然后，题目好像只告诉我们了中序遍历顺序，还信誓旦旦的告诉我们，一定能得出唯一的后序遍历顺序......真是woc啊.....当然，不可能是题目错了，只能是菜鸡还没发现诀窍。

再仔细想想，题目好像确实给了俩个数字序列：push序列+pop序列。有 、意思！emmmm，用样例看看是不是能从这俩个序列里唯一确定一棵树，如图：

 

原来真的可以唯一确定一棵树，想想也应该，因为输入确实“唯一的”遍历了树，不可能有两棵不同的树有同种中序遍历顺序。

问题到这里，本来已经可以写出满足测试的代码了。但是，陈越姥姥曾给我们一个思路：是不是一定要建树？

是否仅仅根据这两行序列，就能直接得到后序遍历的输出？emmmmmm其实确实可以，但是菜鸡当时没那么聪明，还是建树了，再者还想练一下建树的代码。

代码如下：

#include<stdio.h>
#include<stdlib.h>
#define Maxsize 30
int tag=0;  //改变输出格式 
//链式堆栈结构体声明
typedef struct StackNode* Link;
struct StackNode{
	int data;
	Link next;
}; 
//链式树结构体声明
typedef struct TreeNode* BinTree; 
struct TreeNode{
	int data;
	BinTree left;
	BinTree right; 
}; 
//创建树头结点
BinTree CreateTree(int X)
{
	BinTree T=(BinTree)malloc(sizeof(TreeNode));
	T->data=X;
	T->left=NULL;
	T->right=NULL;
	return T;
} 
//建树函数
BinTree BuildTree(int s1[],int s2[],int head,int end,int size,BinTree T,int position)     
//head与end标注当前结点左右儿子在出栈序列中的取值范围 
{	int limit;	
//limit当前结点在出栈序列中的位置,position当前结点在入栈序列中的位置 
	for(int i=0;i<size;i++)
	{
		if(T->data==s2[i])
		{
			limit=i;
			break;
		}
	}
	if(limit>head+1)     //表明当前结点有左儿子 
	{
		BinTree tl=(BinTree)malloc(sizeof(TreeNode));
		tl->data=s1[position+1];
		tl->left=NULL;
		tl->right=NULL;
		T->left=tl; 
		BuildTree(s1,s2,head,limit,size,tl,position+1);
	}
	if(limit<end-1)    //表明当前结点有右儿子
	{
	 	BinTree tr=(BinTree)malloc(sizeof(TreeNode));
	 	tr->data=s1[position+(limit-head)];
	 	tr->left=NULL;
	 	tr->right=NULL;
	 	T->right=tr;
		BuildTree(s1,s2,limit,end,size,tr,position+limit-head);
	} 
	return T;
} 
//堆栈初始化头结点函数
Link CreateStack()
{
	Link P=(Link)malloc(sizeof(StackNode));
	P->next=NULL;
	return P;
} 
//堆栈判空函数
bool IsEmpty(Link T)
{
	if(T->next==NULL)
		return false;
	else
		return true;
} 
//堆栈入栈函数
Link Push(Link T, int X)
{
	Link rear=(Link)malloc(sizeof(StackNode));
	rear->data=X;
	rear->next=T->next;
	T->next=rear;
	return T; 
} 
//堆栈出栈函数
int Pop(Link T)
{	
	if(IsEmpty)
	{
		Link Topitem;
		int Data;
		Topitem=T->next;
		T->next=Topitem->next;
		Data=Topitem->data;
		free(Topitem);
		return Data;	
	}
	else
	{	
		printf("栈空\n");
		return 0; 
	}
}
//树后序遍历函数
void PostOrderTravel(BinTree q)
{	
	if(q){
		PostOrderTravel(q->left);
		PostOrderTravel(q->right);
		if(tag==0)
		{
			printf("%d",q->data);
			tag=1;
		}
		else
		{
			printf(" %d",q->data);
		} 
		
	}
} 
 
int main()
{
	//建立堆栈，根据输入，得到入出栈序列
	int size,number,rear1,rear2;
	rear1=rear2=0;
	Link Top;
	char a[4];
	int s1[Maxsize];//记录入栈序列 
	int s2[Maxsize];//记录出栈序列 
	Top=CreateStack();
	scanf("%d",&size);
	getchar();
	for(int i=0;i<2*size;i++)
	{
		scanf("%s",&a);
		if(a[1]=='u')
		{	
			scanf("%d",&number);
			getchar();
			Push(Top,number);
			s1[rear1]=number; 
			rear1+=1;
		}
		else if(a[1]=='o')
		{
			getchar();
			s2[rear2]=Pop(Top);
			rear2+=1;
		}           
	}
	//根据入出栈序列构造树
	BinTree T=CreateTree(s1[0]);
	BinTree Q=BuildTree(s1,s2,-1,size,size,T,0); 
	//树的后序遍历 
	int tag=0;
	PostOrderTravel(Q); 
} 

测试结果：

总结：苏服啊苏服，还是要去学习一下怎么直接得出后序输出，感觉数学学的更好一点，写的代码能更美更简洁！