时间复杂度（数据结构1）-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_41823495/article/details/133960515

广而告知：博客写得好，Emoji要选好！！🎵 🎶 🔈 🔇 🔉 🔊 🔔 🔕 📣 📢
写博客是知识是巩固和温习，所以在这个信息爆炸的时代，每个人每天都要接收很多讯息，你的记忆是有限的，知识也是有限的，时间也是有限的，既然如此，那是时候磨亮我的五十米大刀了。你很强，上天揽月你不行，你很强，下海捞鱼总行吧！

💀☠💩🤡👹👺👻👽👾🤖 -->渴望知识！！！

1.数据结构和数据库的区别

数据结构：在内存中管理数据。

数据库：在磁盘中管理数据。

2.内存和硬盘存储数据的区别

内存存储速度块，硬盘存储速度慢

内存带电存储，磁盘不需要带电存储。

3.计算中存储方式：内存和磁盘。

4.什么是时间复杂度？

时间复杂度就是找到某条基本语句与问题之间的数字表达式，就是算出了该算法的时间复杂度。

4.1接下来我们看一道题目：

F(N)=N*N+2N+10

N=10,F(N)=130

N=100,F(N)=10210

N=1000,F(N)=1002010

我们时间复杂度是取影响最大的项

大O渐进表示法：估算这道题的复杂度就是O（N^2）

#include <stdio.h>
void func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		for (int j = 0; j < N; ++j)
		{
			++count;
		}
	}
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n",count);
}

int main()
{
	int N = 0;
	//scanf("%d", &N);
	while (scanf("%d", &N) != EOF)
	{
		func1(N);
	}
	return 0;

}

大家可以看一下输入不同的N值，然后输出的结果，是不是满足F(N)=N*N+2*N+10

4.2 接下来我另一道题，时间复杂度是O（N）

F(N)=2N+10

F(10)=2*10+10=30

F(100)=2*100+10=210

F(1000)=2*1000+10=2010

当N是极限大的时候，这个10是可以忽略的，所以时间复杂度就是O(N)

#include <stdio.h>
void func2(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n",count);
}
int main()
{
	int N = 0;
	//scanf("%d", &N);
	while (scanf("%d", &N) != EOF)
	{
		func2(N);
	}
	return 0;
}

看一下编译结果：

4.3 时间复杂度是O(M+N)

O(M+N)

O(MAX(M,N))

如果N>>M(远大于)复杂度就是O（N）

如果M>>n(远大于)复杂度就是O（M）

如果M~=n(约等于)复杂度就是O（M）或O(N)

#include <stdio.h>
void fun3(int M,int N)
{
	int count = 0;
	for (int i = 0; i < M; ++i)
	{
		++count;
	}
	for (int j = 0; j < N; ++j)
	{
		++count;
	}
	printf("%d\n", count);
}
int main()
{
	int M = 0;
	int N = 0;
	//scanf("%d %d", &M, &N);
	while( (scanf("%d%d",&M,&N) != EOF))
	{
		fun3(M,N);
	}
	//fun3(M, N);
	return 0;
}

如果M=10000 N=10

或者N=10,M=10000

4.4 注意O（1）并不是代表一次，而是常数次，最大的项就是常数次。

大O符号，（Big O notation ）:是用于描述函数渐进的数字符号。

那么如何推到大O呢？

4.4.1.用常数1取代运行时间中的所有加法常数

4.4.2.在修改后的运行次数函数中，只保留最高阶项

4.4.3.如果最高阶项存在且不是1，则去除与这个项目相乘的函数，得到的结果就是大O阶。

上题目：

#include <stdio.h>
void fun4(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}
int main()
{
	int N = 0;
	while (scanf("%d", &N) != EOF)
	{
		fun4(N);
	}
	return 0;
}

5.时间复杂度是保守的估计算，取最坏O（N）

最好，最坏，平均

const char *strchr(const char *str,int character)
while (*str)
{
	if (*str == character)
	{
		return str;
	}
	++str;
}

最坏情况：任意输入规模的最大运行次数（上界）

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数（下界）

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索时间复杂度是O（N）

6.冒泡函数的时间复杂度

O（N*(N-1)/2）

7.消失的数字

什么思路求解呢？

7.1思路1：

由于所要找的数字是在0~N之间，那么通过数学关系我们知道，0~N之间的数字之和等于N（N-1）/2 ，想要找到这个区间消失的数字，只需要通过区间数字之和然后减去其他已经出现的数字，那么得到的数字就是消失的那个数字。

？=N(N-1)/2-其他数字；

如果我们把已知的数字存储在nums[10]内，那么只需要使用？=N(N-1)/2-nums[0]-nums[1]-...nums[9]

上代码：

#include <stdio.h>

int missNumber(int* nums, int numsize)
{
	int N = numsize;
	int sum = ((0 + N)*(N+1))/ 2;
	for (int i = 0; i <=numsize; ++i)
	{
		sum =sum -nums[i];
	}
	printf("%d\n", sum);
}
int main()
{
	int nums[10] = { 1,2,3,4,7,9,6,5,0 };
	missNumber(nums, 9);
	return 0;
}

7.2思路2：

通过异或，数字内的每个数字都异或一下就可以将这个数替换掉了。

从而找到那个从未出现过的值。

#include<stdio.h>
int missNumber(int* nums, int numsize)
{
	int x = 0;
	for (int i = 0; i < numsize; ++i)
	{
		x ^= nums[i];
	}

	for (int i = 0; i <=numsize; ++i)  //这里为什么要等于号，那是因为消失的哪一个数字此刻如果要在数组内，那就需要加1，消失的这个值就会被留下来。 
	{
		x ^= i;
	}
	return x;
}
int main()
{
	int c = 0;
	int nums[10] = { 1,2,3,4,7,9,6,5,0 };
	printf("消失的数字是 \n");
	c=missNumber(nums, 9);
	printf("%d\n", c);
	return 0;
}

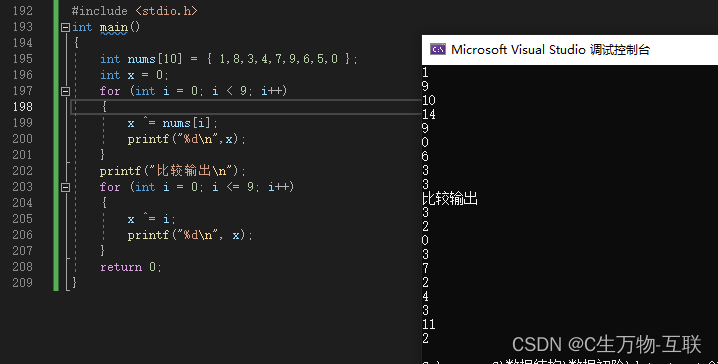
调试看一下：

大家也可以通过下面的方式来调试查看：

#include <stdio.h>
int main()
{
	int nums[10] = { 1,2,3,4,7,9,6,5,0 };
	int x = 0;
	for (int i = 0; i < 9; i++)
	{
		x ^= nums[i];
		printf("%d\n",x);
	}
	printf("比较输出\n");
	for (int i = 0; i <= 9; i++)
	{
		x ^= i;
		printf("%d\n", x);
	}
	return 0;
}

如果数组内拿掉其他数字是不是也可也一样输出：

拿掉2

程序执行之后，找到消失的数字是2

最后，请各位发财的金手指，帮忙点点赞和关注！

💁‍♂️💁‍♀️🙋🙋‍♂️🙋‍♀️🧏🧏‍♂️一赞三连🧏‍♀️🙇🙇‍♂️🙇‍♀️🤦🤦‍♂️🤦‍♀️🤷🤷‍♂️🤷‍♀️

💁‍♂️💁‍♀️🙋🙋‍♂️🙋‍♀️🧏🧏‍♂️一赞三连🧏‍♀️🙇🙇‍♂️🙇‍♀️🤦🤦‍♂️🤦‍♀️🤷🤷‍♂️🤷‍♀️
————————————————
版权声明：本文为优快云博主「C生万物-互联」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/qq_41823495/article/details/133897290