本文深入探讨算法竞赛中的核心技巧，包括快速幂、64位整数乘法、状态压缩、汉密尔顿路径等高级算法的应用。通过具体实例解析，帮助读者掌握高效算法设计与实现，提升算法竞赛水平。
A : [算法竞赛进阶指南]A^B
每一个整数可以唯一表示为若干指数不重复的2的次幂的和。
比如：3^5:5可以表示为:101,3^(1*2^2+0*2^1+1*2^0)
#include <iostream>
#include <algorithm>
using namespace std;
using ll = long long;
// 快速幂
int Pow(int a, int b, int p)
{
int ans = 1 % p;
while (b != 0)
{
if (b & 1)
ans = (ll)ans * a % p;
a = (ll)a * a % p;
b >>= 1;
}
return ans;
}
int main()
{
int a, b, p;
cin >> a >> b >> p;
cout << Pow(a, b, p) << endl;
return 0;
}
B : [算法竞赛进阶指南]64位整数乘法
类似快速幂，把整数b用二进制表示
比如：3*5:3*(1*2^2+0*2^1+1*2^0)
long long mul(long long a, long long b, long long p) {
long long ans = 0;
for (; b; b >>= 1) { // 从低位到高位
if (b & 1) ans = (ans + a) % p; //该位是1，就累加
a = a * 2 % p; // 每一位上，相应的a为2的幂次方
}
return ans;
}
C : A^B II
这道题关键在这一句，防止数据溢出，其他跟快速幂一样
a * b % p = ( a % p ) * ( b % p ) % p;
D : [算法竞赛进阶指南]费解的开关
位进制运算，状态压缩
枚举第一行所有开关的点击状态，然后递推其n-1行的状态
0表示点，1表示不点
#include <iostream>
#include <vector>
using namespace std;
const int INF = 0x3f3f3f3f;
char a[5][6];
int b[5][5];
const int dis[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};
void click(int x, int y)
{
b[x][y] ^= 1;
for (int i = 0; i < 4; i++)
{
int dx = x + dis[i][0];
int dy = y + dis[i][1];
if (dx < 0 || dx >= 5 || dy < 0 || dy >= 5)
continue;
b[dx][dy] ^= 1;
}
}
int main()
{
//freopen("test.txt","r",stdin);
int t;
cin >> t;
while (t--)
{
for (int i = 0; i < 5; i++)
cin >> a[i];
int ans = INF, cnt = 0, flag = 0; //ans表示最少步数，cnt记录当前步数，flag表示当前方案可不可行
for (int i = 0; i < 32; i++) //枚举32种方案
{
for (int k = 0; k < 5; k++)
{
// cout<<a[k]<<endl;
for (int j = 0; j < 5; j++)
b[k][j] = a[k][j] - '0';
}
cnt = 0;
flag = 0;
for (int j = 0; j < 5; j++)
{
if ((i >> j) & 1)
{
cnt++;
click(0, j); //点击第一行的开关
}
}
for (int j = 0; j < 4; j++) //第一行灯亮灭情况固定，改变剩下4行灯的亮灭情况
{
for (int k = 0; k < 5; k++)
{
if (!b[j][k]) //如果前一行某灯是灭的，那通过下一行将前一行灯变亮
{
cnt++;
click(j + 1, k);
}
}
}
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 5; j++)
{
if (!b[i][j]) //遍历所有灯，如果还有未亮的，说明此方案行不通
{
flag = 1;
break;
}
}
if (flag)
break;
}
if (!flag) //说明该方案可行
{
ans = min(ans, cnt);
}
}
//cout<<ans<<endl;
if (ans == INF || ans > 6)
cout << -1 << endl;
else
cout << ans << endl;
}
return 0;
}
E : 获取所有钥匙的最短路径
bfs+状压
这道题多了个状态，每走一步需要记录当前钥匙的状态，可以用二进制01表示没把钥匙的状态。
struct Step
{
int x;
int y;
int ck; //目前手中钥匙的状态
Step(int x,int y,int ck):x(x),y(y),ck(ck){}
};
class Solution {
public:
queue<Step> que;
bool vis[35][35][1<<7]={false}; //标记当前状态是否被拓展
const int dis[4][2]={0,1,1,0,0,-1,-1,0};
int shortestPathAllKeys(vector<string>& grid) {
int len1=grid.size();
int len2=grid[0].length();
int k=0; //记录钥匙的数量
for(int i=0;i<len1;i++)
{
for(int j=0;j<len2;j++)
{
if(grid[i][j]>='a'&&grid[i][j]<='z') k++;
if(grid[i][j]=='@')
{
que.push(Step(i,j,0));
vis[i][j][0]=true;
}
}
}
int steps=0;
while(!que.empty())
{
int l=que.size();
while(l--)
{
Step u=que.front();
que.pop();
for(int i=0;i<4;i++)
{
int dx=u.x+dis[i][0];
int dy=u.y+dis[i][1];
int x=u.ck; //取出当前状态
if(dx>=0&&dx<len1&&dy>=0&&dy<len2)
{
char ch=grid[dx][dy];
if(ch=='#'||vis[dx][dy][x]) continue;
if(ch>='a'&&ch<='z')
{
x=x|(1<<(ch-'a')); //将该位变为1
if(x==((1<<k)-1))
{
return steps+1;
}
}
if(ch>='A'&&ch<='Z')
{
if(!(x>>(ch-'A')&1)) //判断当前位是否是1
{
continue;
}
}
vis[dx][dy][x]=true;
que.push(Step(dx,dy,x));
}
}
}
steps++; //步数加1
}
return -1;
}
};
F : [算法竞赛进阶指南]Hamilton路径
状压dp
dp[i][j]表示在i点处，状态为j下，起点到该点的最短路径
状态0表示不经过，1表示经过
比如dp[3][13],状态13在二进制下是1101，也就是从0到3经过点2，没有过1
在dp过程中，到达该点是从哪个点过来路径最短的，i^1<<j把第j个点的状态取反，即到达第j个点是从状态0101来的
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int INF=0x3f3f3f3f;
int n;
int weight[25][25]; //保存权值
int dp[25][1<<20]; //dp[i][j]表示在i点处，状态为j下，起点到该点最短路径为dp[i][j]
int findMin(int n)
{
memset(dp,INF,sizeof(dp));
dp[0][1]=0; //起点赋初值，只经过了0路径为0
for(int i=1;i<1<<n;i++) //枚举所有状态,在所有状态下，起点到各点的最短路径
{
for(int j=0;j<n;j++)
{
if(i&(1<<j)) //取出状态i中第j个点的状态，如果是1表示经过
{
for(int k=0;k<n;k++) //判断在经过j点前还经过哪些点
{
// i^1<<j把i在二进制下的第j位取反，因为此前还没有到达过j点
if((i^1<<j)>>k&1) //在经过j点前，是否经过第k个点,比如1101，在到达第2个点时，是否经过了第0，1，3点，这个状态表示不经过1点
{
dp[j][i]=min(dp[j][i],dp[k][i^1<<j]+weight[j][k]);
}
}
}
}
}
return dp[n-1][(1<<n)-1];
}
int main()
{
//freopen("test.txt","r",stdin);
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cin>>weight[i][j];
}
}
cout<<findMin(n)<<endl;
return 0;
}
H : [算法竞赛进阶指南]激光炸弹
二维前缀和
5000*5000，卡空间，两个二维数组会爆掉，只能用一个二维数组，先保存数据点，后面直接累加求和。
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + dp[i][j];
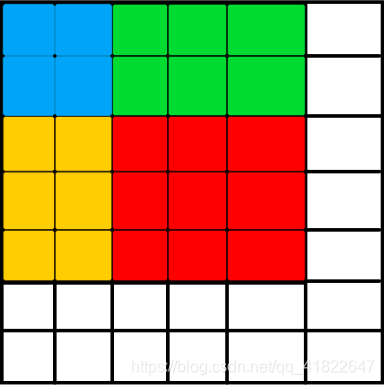
枚举所有边长为R的正方形
ans = max(ans, dp[i][j] - dp[i - m][j] - dp[i][j - m] + dp[i - m][j - m])
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 5005;
// int a[MAXN][MAXN]; //存放价值
int dp[MAXN][MAXN]={0}; //存放二维前缀和
int n, m; //n个目标，边长为m的炸弹，r长度，c宽度
int main()
{
// freopen("test.txt", "r", stdin);
cin >> n >> m;
int len1 = m; //行
int len2 = m; //列
int x, y, k; //坐标，价值
for (int i = 1; i <= n; i++)
{
cin >> x >> y >> k;
dp[x+1][y+1] +=k; //价值累加
len1 = max(len1, x+1);
len2 = max(len2, y+1);
}
for (int i = 1; i <= len1; i++) //二维前缀和,从1开始，方便给边缘的点求和
{
for (int j = 1; j <= len2; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + dp[i][j];
}
}
int ans = 0;
for (int i = m; i <= len1; i++)
{
for (int j = m; j <= len2; j++)
{
ans = max(ans, dp[i][j] - dp[i - m][j] - dp[i][j - m] + dp[i - m][j - m]);
}
}
cout << ans << endl;
return 0;
}
I : [算法竞赛进阶指南]Inc序列
差分
相同的序列，说明最后任意两个数的差为0，可以转成差分使最后序列都为0
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
using ll = long long;
ll nums[100005];
ll dp[100005];
int main()
{
int t;
cin >> t;
for (int i = 1; i <= t; i++)
{
cin >> nums[i];
dp[i] = nums[i] - nums[i - 1];
}
ll s1 = 0, s2 = 0;
for (int i = 2; i <= t; i++)
{
if (dp[i] > 0)
s1 += dp[i]; //需要减1的次数
else
s2 -= dp[i]; //需要加1的次数
}
cout << max(s1, s2) << endl;
cout << abs(s1 - s2) + 1 << endl;
return 0;
}
J : 供暖气
二分查找每间房子到最近暖气的最短距离，最后所有距离取最大值
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int INF=0x3f3f3f3f;
class Solution
{
private:
int n, m;
vector<long long> Heaters;
vector<long long> Houses;
public:
Solution(int n, int m)
{
this->n = n;
this->m = m;
}
void addHouses(int x)
{
Houses.push_back(x);
}
void addHeaters(int x)
{
Heaters.push_back(x);
}
int finfRadius()
{
sort(Heaters.begin(),Heaters.end());
long long ans = 0;
for (int i = 0; i < Houses.size(); i++)
{
long long cur = INF;
// 返回第一个不小于x的迭代器
auto l = lower_bound(Heaters.begin(), Heaters.end(), Houses[i]);
if (l != Heaters.end()) //房子右边有暖气
{
cur = *l - Houses[i];
}
if (l != Heaters.begin()) //房子左边有暖气
{
auto s = l - 1; //左边暖气位置
cur = min(cur, Houses[i] - *s); //两个距离取最小的那个
}
ans = max(cur, ans);
}
return ans;
}
};
int n, m;
int main()
{
freopen("test.txt","r",stdin);
cin >> n >> m;
Solution sol(n, m);
for (int i = 0; i < n; i++)
{
long long a;
cin >> a;
sol.addHouses(a);
}
for (int j = 0; j < m; j++)
{
long long a;
cin >> a;
sol.addHeaters(a);
}
cout << sol.finfRadius() << endl;
return 0;
}
K : 线性筛素数
模版使用
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
const int MAX_N = 10000001;
int v[MAX_N], prime[MAX_N]; //prime数组存放质数，v数组用来标记
void primes(int n)
{
memset(v, 0, sizeof(v)); // 最小质因子
int m = 0; // 质数数量
for (int i = 2; i <= n; i++)
{
if (v[i] == 0)
{ // i是质数
v[i] = i;
prime[++m] = i;
}
// 给当前的数i乘上一个质因子
for (int j = 1; j <= m; j++)
{
// i有比prime[j]更小的质因子，或者超出n的范围
if (prime[j] > v[i] || prime[j] > n / i)
break;
// prime[j]是合数i*prime[j]的最小质因子
v[i * prime[j]] = prime[j];
}
}
}
int n, m;
int main()
{
// freopen("test.txt","r",stdin);
cin >> n >> m;
primes(n);
while (m--)
{
int t;
cin >> t;
if (t == v[t])
cout << "Yes" << endl;
else
cout << "No" << endl;
}
return 0;
}
L : [算法竞赛进阶指南]最佳牛围栏
M : [蓝桥杯][历届试题]最大子阵
降维 动态规划
枚举所有可能的组合情况，按列累加，转变成一维的求最大子序和问题
求最大子序和
class Solution {
public:
int maxSubArray(vector<int>& nums) {
vector<int> dp(nums.size(),0);
int m=0,maxn=nums[0];
for(int i=0;i<nums.size();i++)
{
if(m>0) m+=nums[i]; //m是正数接着往上加
else m=nums[i]; //m是负数那就不要再加了，因为负数会拉低nums[i]的数值
maxn=max(maxn,m);
}
return maxn;
}
};
动态规划做法
-1 -4 3
3 4 -1
-5 -2 8
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
int findMax(int *arr,int n) //转变为求最大子序和的一维问题
{
int maxn=arr[0],m=0;
for(int i=0;i<n;i++)
{
if(m>0) m+=arr[i];
else m=arr[i];
if(maxn<m) maxn=m;
}
return maxn;
}
int dp[505][505];
int arr[505];
int main()
{
// freopen("test.txt","r",stdin);
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>dp[i][j];
}
}
//枚举所有组合情况
int maxn=dp[0][0];
for(int i=0;i<n;i++)
{
fill(arr,arr+n,0); //每次要清0
for(int j=i;j<m;j++)
{
for(int k=0;k<n;k++)
arr[k]+=dp[k][j]; //累加k行j列
int m=findMax(arr,n);
maxn=max(m,maxn);
}
}
cout<<maxn<<endl;
return 0;
}
前缀和+lis
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
int dp[505][505]; //dp[i][j]:j列前i行的前缀和
int n, m;
const int INF = 0x3f3f3f3f;
int main()
{
// freopen("test.txt","r",stdin);
cin >> n >> m;
int maxSum = -INF;
bool flag = false;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> dp[i][j];
if (dp[i][j] < 0)
{
maxSum = max(maxSum, dp[i][j]);
}
else
flag = true; //不全负
dp[i][j] += dp[i - 1][j];
}
}
if (flag == false)
cout << maxSum << endl;
else
{
int ans = 0;
for (int i = 1; i <= n; i++) //枚举所有可能的组合
{
for (int j = i; j <= n; j++)
{
int maxn = 0;
for (int k = 1; k <= m; k++)
{
maxn += (dp[j][k] - dp[i - 1][k]);
if (maxn < 0)
maxn = 0;
ans = max(maxn, ans);
}
}
}
cout << ans << endl;
}
return 0;
}
扫一扫
1046
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
