kaggle竞赛之Hungry Geese比赛

ReEchooo

已于 2022-02-24 09:32:44 修改

阅读量1.6k

点赞数 1

分类专栏：比赛记录文章标签：机器学习 python 人工智能

于 2021-08-11 11:03:19 首次发布

本文链接：https://blog.youkuaiyun.com/qq_41773233/article/details/119137380

版权

比赛记录专栏收录该内容

2 篇文章

订阅专栏

kaggle竞赛之Hungry Geese比赛

1. 比赛内容和规则
- 1.1 比赛内容
- 1.2 比赛规则
2. 强化学习算法思路
- 2.1 HandyRL
- 2.2 蒙特卡罗树搜索
3. 经验总结

本文主要记录参加kaggle竞赛的强化学习赛道的算法思路。此次竞赛我们排名为57/875，获得一枚铜牌。

1. 比赛内容和规则

本章简要介绍Hungry Geese比赛内容和规则，能够让新手快速了解kaggle竞赛的大致流程。

1.1 比赛内容

Hungry Geese比赛（比赛链接）就是我们小时候玩的贪吃蛇游戏，如下图所示，游戏的格子大小为7*11，每局比赛有4只goose和一些随机放置的食物，goose每吃一个食物长度就会加1，每走40步goose长度会减1（goose长度最小为1，此后不再减），游戏持续时间最多200秒（也就是goose最多走两百步），在游戏中会保证每一秒场面上都存在2个食物。

如果一只goose的头撞到自己的身体，或者别的goose的身体，都会立即“死亡”，退出比赛。如果两个goose的头相撞，则同时“死亡”。

评价一局比赛中goose的好坏，是根据goose存活的时间和goose“死亡”时的长度，一般来说，存活时间越长，kaggle平台会认为这个goose越好，在存活时间相同的前提下，才会比较长度。

在这里插入图片描述

每只goose只需要根据当前场面状态，输出 NORTH, SOUTH, EAST, or WEST中的一个动作即可，每个动作的计算时间为1s，超出1s的时间被算作“超出时间”，“超出时间”的累计不能超过60s，否则将取消goose的继续比赛资格。

leaderboard上的评分是根据每局的对局情况进行算分的，初始提交的goose评分为600分，然后kaggle平台会根据当前goose的评分匹配评分相近的对手，也就是自己提交的goose会和三个不同人提交的goose进行比赛，如果在一局比赛中获得第一名评分会增加，获得第四名评分会减少，中间两名有时会增加有时会减少，因为这个评分代表goose能力的均值，比赛次数越少，均值加（减）的越多，方差越大，比赛次数越多，均值加（减）的越少，方差越小。

1.2 比赛规则

比赛要求提交应该是一个python文件，最后一个’def’接受一个obs, 并返回一个action。

比赛的前11名为金牌，11至50名为银牌，50至100名为铜牌。

2. 强化学习算法思路

此次竞赛我们尝试过使用DuelingDQN， DQN，PPO等常用的强化学习算法，但是并没有取得较好的评分，都在700分以下。

此次竞赛长期霸居榜首的参赛者分享了他们的开源库——handyRL，通过此库训练出来的agent在此次竞赛中取得较好的成绩，agent的评分能达到940分，可以说是相当不错了。

下面首先介绍此开源强化学习库——HandyRL，然后介绍基于handyRL的蒙特卡罗树搜索算法。

2.1 HandyRL

HandyRL的GitHub链接为：https://github.com/DeNA/HandyRL，如何配置环境以及如何设置训练参数在GitHub中都已经讲得比较清楚了，这里只做简单介绍。

HandyRL主要提供off-policy的policy gradient算法。使用者可以用一些off-policy变种的更新方法（基于策略目标，和基于价值目标），从传统的更新方法（monte carlo，TD( $\lambda$ )）到新型的更新方法(V-Trace, UPGO)都是可以的。这些选项都可以在config.yaml文件中修改。

HandyRL选择了learner-worker的训练架构，与IMPALA类似（IMPALA的介绍可以参照：【强化学习 44】IMPALA/V-trace）。Learner是训练核心，它用来更新模型并控制worker们。worker们有两个角色，分别是异步地生成episodes (或者说trajectories)，以及评估训练模型。在生成一个episode时，默认使用self-play，即自博弈。

在HandyRL的config.yaml中，我们设置的参数如下（程序需要在8G以上的GPU上运行）：
在这里插入图片描述

这里介绍一下几个关键参数：

gamma是强化学习中的折扣因子，关注未来长期的回报
forward_steps是在做价值估计(状态价值 $v (s)$ , 或者动作价值 $q (s, a)$ ) 或者优势函数估计 $a (s, a) = q (s, a) - v (s)$ 时，需要向后看的步数。以动作价值为例，即：
$q\left( S_t,A_t \right) =R_{t+1}+\gamma R_{t+2}+\cdots +\gamma ^{n-1}R_{t+n}+\gamma ^nq\left( S_{t+n},A_{t+n} \right)$
其中：n即为forward_steps的值
update_episodes代表间隔多少个episode后更新并保存模型，一个epoch是这么多个episode。
minimum_episodes代表经验池中存储的最少episodes的量，因为是off-policy，所以更新后的model可以使用更新前的数据进行学习，这个值最好设大一点，等待经验池有足够多的数据再进行更新。
maximum_episodes代表经验池中存储的最大episodes的量，如果超出这个值，那么最旧的episodes将会被剔除掉。
epochs代表停止训练的epoch次数，如果此值为负，那么会一直训练，每训练一个epoch就回评估并保存一次模型
lambda即为TD( $\lambda$ )中的 $\lambda$ ，当 $\lambda=0$ 时，即为单步TD方法，当 $\lambda=1$ 时，即为monte carlo方法，详情可以参照：强化学习入门第四讲时间差分法（TD方法），和强化学习实践五 SARSA(λ)算法实现。
policy_target代表使用什么方法训练目标策略。这里使用的是TD法。
value_target代表使用什么方法训练目标价值。这里使用的是TD法。
restart_epoch代表重新开始训练的epoch，这个是用来接着继续训练的参数，比如上次训练在epoch12结束，那么这里设置restart_epoch=12，就可以接着上次的继续训练。

值得注意的是，在handyRL的learner类中有一个很重要的属性：model_class，它直接决定了等下需要训练的模型类型。对于HungryGeese游戏，此模型类型为GeeseNet，下面来看GeeseNet的定义。

在这里插入图片描述

GeeseNet网络的forward输出为策略p（即东南西北四个方向的概率）和状态价值v。
在这里插入图片描述

注意forward方法的输入x是经过处理的，处理方式如下。简单来说就是把 $7 * 11$ 的图像变成 $17 * 7 * 11$ 的ndarray数据，其中 $0\sim3$ 是四只goose头的位置， $4\sim7$ 是四只goose尾的位置， $8\sim11$ 是四只goose全身的位置。 $12\sim15$ 是上一次四只goose头的位置，16是食物的位置。

在这里插入图片描述

forward方法中的h变量是对输入进行特征提取，其中采用一个TorusConv2d类（如下图所示），handyRL把它当做神经网络——GeeseNet网络的一个模块。

在这里插入图片描述

此模块表面上看就是一个卷积模块+批归一化处理，但其中还有一个h处理的小细节，即在做卷积前，对nparray数组进行了扩增处理。

以下两句：

        h = torch.cat([x[:,:,:,-self.edge_size[1]:], x, x[:,:,:,:self.edge_size[1]]], dim=3)
        h = torch.cat([h[:,:,-self.edge_size[0]:], h, h[:,:,:self.edge_size[0]]], dim=2)

等效于对一个数组（或者理解为图像）
在这里插入图片描述
扩增后为：

在这里插入图片描述

这个是为Hungry Geese比赛专门设计的，因为7*11的格子中并没有“边界”的概念，当goose在最上面一行再往上走一步时，就会移动到最下面一行，而这个扩展就是为了在后续做卷积时能够真实地反映这个情况，如果这里用卷积常用的边界“补零”操作，很可能训练得到的agent不会选择穿过边框。

继续回到forward方法上来，可以看到特征提取后，还进行了如下操作：

        h_head = (h * x[:,:1]).view(h.size(0), h.size(1), -1).sum(-1)
        h_avg = h.view(h.size(0), h.size(1), -1).mean(-1)

第一行语句是在goose的头部位置收集特征。第二行语句是在goose的所有身体位置收集特征。

需要把头部单独列出来，是因为在《Hungry Geese》中，通常情况下，goose头部周围的状态对于选择行动和生死检测是最重要的，像素距离头部越远，状态的重要性就越低。

但是，对于价值估计来说，包括每只goose的长度在内的全局信息也很重要。这也就是为什么头部特征和平均特征在最后一层估值之前被连接起来。

我们的模型核心就是GeeseNet，至此GeeseNet已介绍完毕，GeeseNet在动作概率（p）估计和状态价值（v）估计上，都有较好的准确性。GeeseNet在训练的时候是采用self-play的方式，也就是自博弈，自己和自己训练的模型对抗，计算价值估计 $V (s)$ 和优势函数估计 $A (s)$ 的方式都是使用TD( $\lambda$ )，同时采用 $\epsilon \times A(s)$ 的方式 进行策略优势估计（因为之前参数选择的是TD( $\lambda$ )方式）。计算loss的方式是用估计值和网络预测值进行比较，用均方差或者F.smooth_l1_loss方式进行计算

详细的训练过程可以参考HandRL源码，部分源码展示如下所示：

计算loss主函数
在这里插入图片描述

在这里插入图片描述

计算loss主函数return的函数
在这里插入图片描述

loss反向传播：
在这里插入图片描述

2.2 蒙特卡罗树搜索

根据前文所述，通过handyRL训练出来的agent不仅能够估计出各个动作（东南西北）运动的概率，还能够估计出当前局面（状态）的价值。如果直接选择agent估计的动作概率最大值作为实际执行的动作，那么得到的agent评分在920分左右，但是加了蒙特卡罗树搜索，agent的评分能达到1100分。究其原因是，蒙特卡罗树搜索是根据实际状态（子节点）的价值和探索次数来综合判定选择哪个动作（对于此竞赛，因为agent还预测了每个动作的概率，所以在搜索过程中还增加了动作概率值这一指标），从而能够做出最优的动作。

如果不了解蒙特卡罗树搜索，可以参考：【最佳实战】蒙特卡洛树搜索算法，如何学习蒙特卡罗树搜索（MCTS），【MCTS】Youtube上迄今为止最好的蒙特卡罗树搜索讲解

蒙特卡罗树搜索（Monte Carlo tree search）的核心是四个：选择(Selection)，拓展(Expansion)，模拟(Simulation，或者说 rollout)，反向传播(Back Propagation)。注意在使用蒙特卡罗树搜索时，不一定要维护一个“树”的数据结构，可以使用“字典”的方式维护。因为此竞赛一个父节点会对应4个子节点，并且会在子节点与子节点的连线上存储“状态动作对的价值”，所以采用字典的方式存储可以避免重复计算此价值。

可以定义一个蒙特卡罗树搜索的类，MCTS，其初始化如下：

在这里插入图片描述

Qsa（由神经网络预测输出）记录(s,a)的价值，对于此竞赛为Qsa[(s,i,a)]，记录(s,i,a)的价值，i为四只goose的编号
Nsa记录访问(s,a)的次数，对于此竞赛为Nsa[(s,i,a)]，记录访问(s,i,a)的次数，i为四只goose的编号
Ns记录访问(s)的次数，对于此竞赛为Ns[s]，记录访问(s)的次数
Ps（由神经网络预测输出）记录状态(s)下采取的策略(即选择四个动作的各自概率)，对于此竞赛为Ps[(s,i)]记录(s,i)下采取的策略，i为四只goose的编号
Vs记录状态(s)的合理移动（或者说可行动作），对于此竞赛，它总是4*1的张量，且由True/Flase组成，对于此竞赛为Vs[(s,i)]记录(s,i)下的合理移动，i为四只goose的编号

然后定义MCTS的动作输出，如下所示：

在这里插入图片描述

它根据在某一状态s下，动作a（东南西北）选取的次数，来决定最后输出的动作概率。如果在曾经的蒙特卡罗树搜索中，某一动作选取的次数最多，那么此动作被选取的概率最大。由于在此竞赛中，为了尽可能地选取最优动作，我们直接选取概率最大的动作作为最终goose的动作，而不再基于概率采样了。

在getActionProb函数中，最核心的代码是：

        while time.time() - start_time < timelimit:
            self.search(obs, self.last_obs)

因为goose在判断选择哪个动作时有时间显示，所以做树搜索时也需要加上时间显示。接下来详细讲述MCTS的search方法。

search方法中完成了蒙特卡罗树搜索的选择，拓展，模拟，反向传播四个操作，我将拆解此代码，并结合“搜索树”讲述如何实现这四个操作。

    def search(self, obs, last_obs):
        s = self.game.stringRepresentation(obs)

        if s not in self.Ns:
            values = [-10] * 4
            for i in range(4):
                if len(obs.geese[i]) == 0:
                    continue
                    
                # leaf node
                self.Ps[(s, i)], values[i] = self.nn_agent.predict(obs, last_obs, i)
                    
                valids = self.game.getValidMoves(obs, last_obs, i)    
                self.Ps[(s, i)] = self.Ps[(s, i)] * valids  # masking invalid moves
                sum_Ps_s = np.sum(self.Ps[(s, i)])
                if sum_Ps_s > 0:
                    self.Ps[(s, i)] /= sum_Ps_s  # renormalize

                self.Vs[(s, i)] = valids
                self.Ns[s] = 0
            return values

        best_acts = [None] * 4
        for i in range(4):
            if len(obs.geese[i]) == 0:
                continue
            
            valids = self.Vs[(s, i)]
            cur_best = -float('inf')
            best_act = self.game.actions[-1]

            # pick the action with the highest upper confidence bound
            for a in range(self.game.getActionSize()):
                if valids[a]:
                    if (s, i, a) in self.Qsa:
                        u = self.Qsa[(s, i, a)] + self.cpuct * self.Ps[(s, i)][a] * math.sqrt(
                                self.Ns[s]) / (1 + self.Nsa[(s, i, a)])
                    else:
                        u = self.cpuct * self.Ps[(s, i)][a] * math.sqrt(
                            self.Ns[s] + self.eps)  # Q = 0 ?

                    if u > cur_best:
                        cur_best = u
                        best_act = self.game.actions[a]
                        
            best_acts[i] = best_act
        
        next_obs = self.game.getNextState(obs, last_obs, best_acts)
        values = self.search(next_obs, obs)

        for i in range(4):
            if len(obs.geese[i]) == 0:
                continue
                
            a = self.game.actions.index(best_acts[i])
            v = values[i]
            if (s, i, a) in self.Qsa:
                self.Qsa[(s, i, a)] = (self.Nsa[(s, i, a)] * self.Qsa[
                    (s, i, a)] + v) / (self.Nsa[(s, i, a)] + 1)
                self.Nsa[(s, i, a)] += 1

            else:
                self.Qsa[(s, i, a)] = v
                self.Nsa[(s, i, a)] = 1

        self.Ns[s] += 1
        return values

如下图所示（下图中的a1，a2，a3，a4分别代表东南西北），假设在初始状态s1时采取了动作a1，进入了状态s2，并且状态s2之前已经见过。

在这里插入图片描述

因为s2见过，所以将直接跳过第一个if判断，进入以下代码：


        # 如果见过，那么从可行动作中选择最佳动作，它不仅考虑自身的最佳动作，还考虑其他goose的最佳动作
        best_acts = [None] * 4
        for i in range(4):
            if len(obs.geese[i]) == 0:
                continue
            
            valids = self.Vs[(s, i)]
            cur_best = -float('inf')
            best_act = self.game.actions[-1]

            # pick the action with the highest upper confidence bound
            for a in range(self.game.getActionSize()):
                if valids[a]:
                    if (s, i, a) in self.Qsa:
                        u = self.Qsa[(s, i, a)] + self.cpuct * self.Ps[(s, i)][a] * math.sqrt(
                                self.Ns[s]) / (1 + self.Nsa[(s, i, a)])
                    else:
                        u = self.cpuct * self.Ps[(s, i)][a] * math.sqrt(
                            self.Ns[s] + self.eps)  # Q = 0 ?

                    if u > cur_best:
                        cur_best = u
                        best_act = self.game.actions[a]
                        
            best_acts[i] = best_act

这段代码对应选择操作，即考虑s2的所有可行动作（这里假设四个动作都可行），对于一只goose在所有可行动作中应该选取哪个动作？它基于以下预测-信任动作上界原则，计算可行动作的u值，选择u值最大的动作：

在这里插入图片描述

这里假设在状态s2下选取动作a2，并且其它的三个goose也按这个原则进行动作选择，这样就可以预测下一游戏局面。下面代码就是进行预测，从而进行树的更深层次的搜索：

        # 考虑所有geese都做了最佳动作后的情形（纳什均衡原则），预测后一步的观测next_obs
        next_obs = self.game.getNextState(obs, last_obs, best_acts)

        # 考虑后一步观测next_obs中所有状态的价值
        values = self.search(next_obs, obs)

值得注意的是，这里又调用了search方法，也就是递归调用。如果预测的下一状态又见过，那么就按照刚才的选择步骤继续，如果没见过，则进入拓展和仿真操作。

如下图所示，假设在状态s2时采取的动作为a2，然后进入了状态s6，但是s6这个状态并没有遇到过，那么就进行树的拓展。树的拓展做三件事情：一是标记这个状态来过（即改变Ns），二是记录这个状态下的合理动作（即改变Vs），三是记录这个状态下的合理动作的选取概率（即改变Ps）。

而仿真则是返回这个状态的价值估计（由handyRL的agent完成）。在原始的蒙特卡罗树搜索的原理中，仿真应该是没有遇到过的状态一直仿真模拟到最终状态，得到一个准确的状态价值，但是这里用神经网络的价值估计代替了。

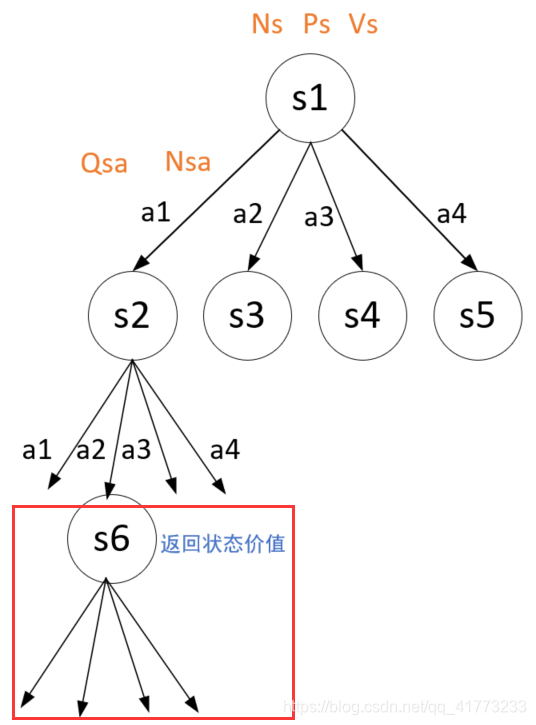
在这里插入图片描述

拓展和仿真操作对应以下代码段落，它也是递归函数的终止条件：


        s = self.game.stringRepresentation(obs) # s代表当前局面中goose的身体位置以及食物位置

        # 如果当前局势s（由各个geese占据的位置和食物位置组成）没有见过，那么加上这个局势，并对这个局势进行估计，返回状态价值
        if s not in self.Ns:
            values = [-10] * 4
            for i in range(4):
                if len(obs.geese[i]) == 0:
                    continue
                    
                # leaf node
                self.Ps[(s, i)], values[i] = self.nn_agent.predict(obs, last_obs, i)
                    
                valids = self.game.getValidMoves(obs, last_obs, i)    
                self.Ps[(s, i)] = self.Ps[(s, i)] * valids  # masking invalid moves，不合理的移动概率直接变为0
                sum_Ps_s = np.sum(self.Ps[(s, i)])
                if sum_Ps_s > 0:
                    self.Ps[(s, i)] /= sum_Ps_s  # renormalize，对于合理的移动，概率重新进行归一化

                self.Vs[(s, i)] = valids # 保存各个动作的合理性
                self.Ns[s] = 0      # 当前局势保存，访问次数初始化为0
            return values

得到未遇见的状态的价值估计后，即进入反向传播操作，开始更新路径上的数据。注意沿途的Qsa值（状态动作对的价值）和Nsa值（状态动作对出现的次数）都需要更新，而这个更新有一个技巧，从代码中可以看到，最后返回的values其实就是前面在仿真simulation中的values，因为沿途上的Q值只需要因为这个s6的价值的出现而更新即可，更新公式即：

$Q\left( s,a \right) =Q\left( s,a \right) +\frac{1}{N\left( s,a \right)}\left( G-Q\left( s,a \right) \right)$

其中G即为values中的一个元素v，因为这里考虑了四条goose，所以values中有四个元素，分别代表各个goose的状态价值。

当然路径上的状态出现次数Ns值也需要更新。

在这里插入图片描述

反向传播操作对应如下代码：



        # 更新状态动作对s-a的价值Qsa，以及访问次数Nsa
        for i in range(4):
            if len(obs.geese[i]) == 0:
                continue
                
            a = self.game.actions.index(best_acts[i])
            v = values[i]
            if (s, i, a) in self.Qsa:
                self.Qsa[(s, i, a)] = (self.Nsa[(s, i, a)] * self.Qsa[
                    (s, i, a)] + v) / (self.Nsa[(s, i, a)] + 1)
                self.Nsa[(s, i, a)] += 1

            else:
                self.Qsa[(s, i, a)] = v
                self.Nsa[(s, i, a)] = 1

        self.Ns[s] += 1

        # 返回后一步观测next_obs中所有状态的价值
        return values