http://codeforces.com/contest/1132/problem/E
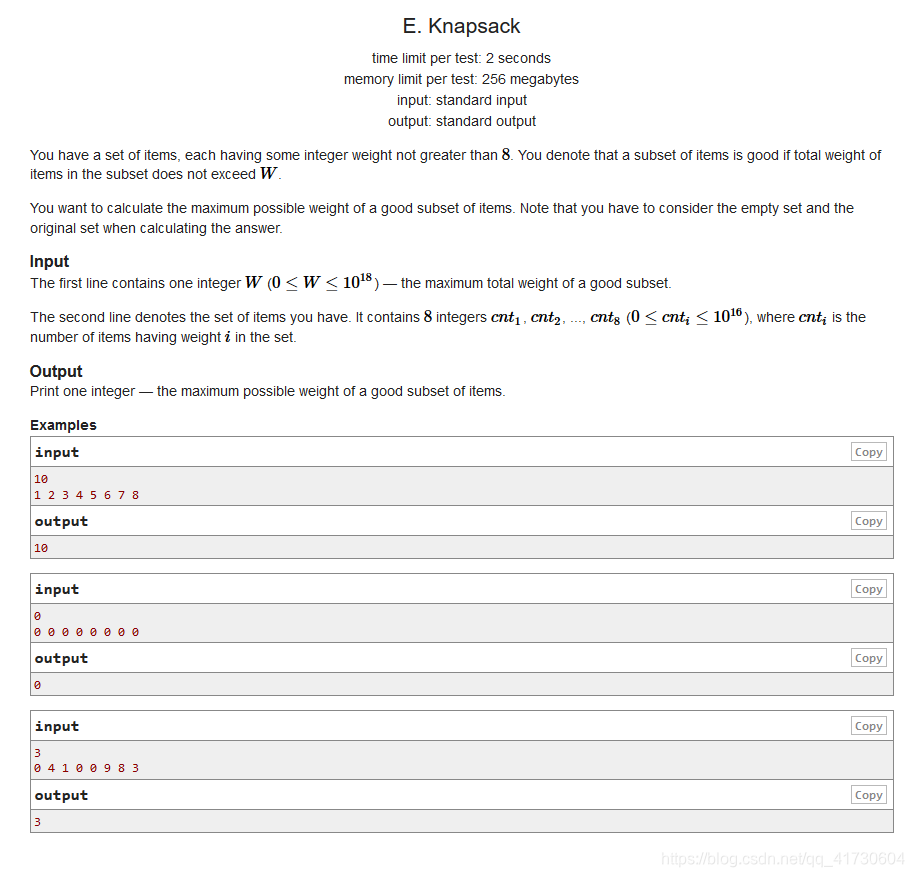
首先,求出(1-8)的LCM,将w分成若干个背包。
令cnt[i]∗i = ki * LCM + qi 。qi的取值范围就是(0-LCM-1)
求出所有的 ∑qi 的情况下,使得 ∑ki 最大。
定义dp[i][j] 到第i个数,背包累计放入j容量时,∑ki的数量。
dp[i][j]=max(dp[i][j],dp[i-1][j-k*i]+(cnt[i]-k)/(lcm/(LL)i));最后遍历i==8时,j的所有情况下,合理答案的最大值。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
const LL lcm=840;
LL w,cnt[10];
LL dp[10][lcm*8+5];
int main(){
ios::sync_with_stdio(false);
cin>>w;
for(int i=1;i<=8;i++) {
cin>>cnt[i];
}
memset(dp,-1,sizeof(dp));
dp[0][0]=0;
for(int i=1;i<=8;i++){
for(int j=0;j<8*lcm;j++){
LL xx=min(lcm/i-1,cnt[i]);
for(int k=0;k<=xx;k++){
if(j-k*i>=0&&dp[i-1][j-k*i]!=-1)
dp[i][j]=max(dp[i][j],dp[i-1][j-k*i]+(cnt[i]-k)/(lcm/(LL)i));
}
}
}
LL ans=0;
for(LL i=0;i<8*lcm;i++){
if(dp[8][i]==-1||i>w) continue;
ans=max(ans,i+lcm*min(dp[8][i],(w-i)/lcm));
}
cout<<ans;
return 0;
}然后还有一种爆搜的办法,比如8个1可以转化为1个8,各种奇怪的转换方式就可以dfs了?
(还没想清楚)
#include <bits/stdc++.h>
using namespace std;
long long cnt[10];
long long w, ans;
void dfs(int pos, long long c){
long long rec;
if (pos > 8){
ans = max(ans, w - c);
return;
}
rec = min(cnt[pos], c / pos);
for (long long i = rec; i >= max(rec - 8, 0LL); i--)
dfs(pos + 1, c - i * pos);
}
int main(){
cin >> w;
for (int i = 1; i <= 8; i++) cin >> cnt[i];
ans = 0;
dfs(1, w);
cout << ans << '\n';
return 0;
}










 本文深入解析 Codeforces 1132E 的背包问题,采用动态规划方法求解最优解,通过计算背包容量与物品数量的关系,找到使∑ki最大的所有∑qi组合。同时探讨了另一种深度优先搜索策略。
本文深入解析 Codeforces 1132E 的背包问题,采用动态规划方法求解最优解,通过计算背包容量与物品数量的关系,找到使∑ki最大的所有∑qi组合。同时探讨了另一种深度优先搜索策略。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








