随机信号处理AR模型Yule_Walker方程直接解法和Levinson_Durbin递推法的MATLAB与Python实现

最新推荐文章于 2025-05-05 12:13:25 发布

Shangzibin666

最新推荐文章于 2025-05-05 12:13:25 发布

阅读量1.8w

点赞数 16

CC 4.0 BY-SA版权

文章标签： AR模型 Yule_Walker Levinson_Durbin MATLAB Python

本文链接：https://blog.youkuaiyun.com/qq_41720125/article/details/93125013

AR模型

AR模型的系统函数H(z)可以表示为：
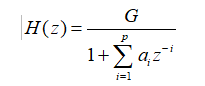
在这里插入图片描述
我们的目的就是要求解系统函数的参数a和增益G。

Yule_Walker方程

矩阵形式
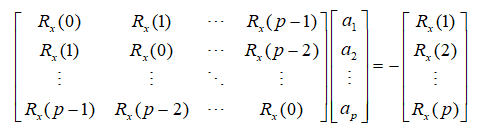
在这里插入图片描述
根据生成的矩阵，可以解出p个参数，再根据自相关函数，可以求出系统增益G。
Yule_Walker方程也可以写成：

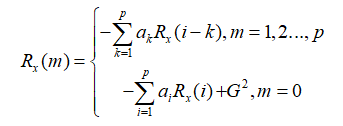
Levinson-Durbin快速递推法

可以看出通过矩阵求逆解Yule-Walker方程的运算量很大，通过观察可以看出Yule_Walker方程的自相关矩阵有一系列良好的性质，可以通过递推的方法求p个参数，从而避免矩阵求逆的运算，减少运算量。
令p=1，可以得到1阶AR模型Yule-Walker方程：
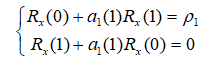
在这里插入图片描述
同理，令p=2，3，4…，将不断变化的p用m表示，可以得到m阶AR模型参数Levinson-Durbin递推算法：

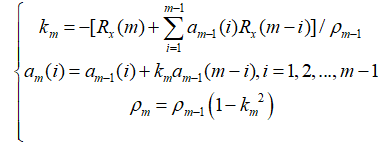
MATLAB实现

Yule_Walker方程

clear
clc
% N = 128;
% p = 64;
N = input('请选择采样点数N:');
p = input('请选择AR模型阶数p（建议N/3<p<N/2):');
n = 0:N-1;
dt = 1;t = n*dt;
xn = 2^0.5*sin(2*pi*0.1*t+pi/3) + 10*sin(2*pi*0.13*t+pi/4); %+ randn(1,N);
R = xcorr(xn,'biased');% 求xn的自相关函数
Rx = zeros(1,p+1);% 预分配内存
% 取对称序列的后半部分
for i = 1:p+1
    Rx(i) = R(i+N-1);
end
Rx
Rmatl = zeros(p,p);
% 生成p个方程对应的矩阵式
for m = 1:p
    for n = 1:p
        Rmatl(m,n) = Rx(max(m,n)-min(m,n)+1);
    end
end
Rmatl
Rmatr = zeros(p,1);
for m = 1:p
    Rmatr(m,1) = -Rx(m+1);
end
% 输出参数ai
ai = (inv(Rmatl)*Rmatr)';% (Rmatl\Rmatr)'
% 根据自相关函数和ai求解系统增益
G = Rx(1);
for i = 1:p
    G = G+ai(i)*Rx(i);
end
fprintf('系统增益G=%f\n',G^0.5);
[H,w] = freqz(G^0.5,[1,ai],N);% 在2*pi范围内N个等分点求系统函数
% Px = (G^0.5)*(abs(H)).^2;
Hf = abs(H);
f = w/(2*pi);
plot(w/(2*pi),Hf);
[magsor,fsor]