B - Closest Common Ancestors(LCA tarjan离线算法)

关于前向星的原理 看这里
关于LCA的tarjan算法戳这里
Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)
Input
The data set, which is read from a the std input, starts with the tree description, in the form:
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 … successorn
…
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) …

The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
Output
For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
For example, for the following tree:

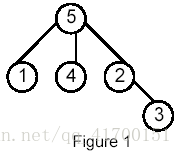
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint
Huge input, scanf is recommended.
题意：找最近公共祖先，如图1和4的是5

基本思路：
1.从根节点开始。
2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。
3.若是v还有子节点，返回2，否则下一步。
4.合并v到u上。
5.寻找与当前点u有询问关系的点v。
6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

Code:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<set>
#include<map>
#include<vector>
using namespace std;
#define ll long long
#define MAX 1000
struct node
{
    int next;
    int to;
} edge[MAX+50];
int head[MAX+50];
bool vis[MAX+50];   //标记数组，标记有没有被访问过
bool root[MAX+50];  //找根节点
int father[MAX+50];  //存的是父亲节点
int ans[MAX+50];    //存的是答案
vector <int> vv[MAX];  //vector相当于二维数组来用
int n;
int cnt;
int roott;


int Find(int x)      
{
    if(x!=father[x])
        father[x]=Find(father[x]);
    return father[x];
}

void Join(int x,int y)
{
    int fx=Find(x),fy=Find(y);
    if(fx!=fy)
        father[fy]=fx;
}

void add_edge(int x,int y)
{
    edge[cnt].to=y;
    edge[cnt].next=head[x];
    head[x]=cnt++;
}

void init()
{
    cnt=0;
    memset(head,-1,sizeof(head));
    memset(vis,false,sizeof(vis));
    memset(root,false,sizeof(root));
    memset(ans,0,sizeof(ans));
 //   scanf("%d",&n);
    for(int i=1; i<=n; i++)
        vv[i].clear();
    for(int i=0; i<=n; i++)
        father[i]=i;
    for(int i=1; i<=n; i++)
    {
        int x,y,m;
        scanf("%d:(%d)",&x,&m);
        if(m==0)
            continue;
        for(int j=0; j<m; j++)
        {
            scanf(" %d",&y);
            add_edge(x,y);
            root[y]=true;
        }
    }
    for(int i=1; i<=n; i++)
        if(root[i]==false)
            roott=i;

}
void LCA(int u)
{
    for(int i=head[u]; ~i; i=edge[i].next)
    {
        int v=edge[i].to;
        LCA(v);
        Join(u,v);
        vis[v]=true;
    }
    for(int i=0; i<vv[u].size(); i++)
    {
        int w=vv[u][i];
        if(vis[w]==true)
        {
            int lca=Find(w);
            ans[lca]++;
        }
    }
}

int main()
{

    while(scanf("%d",&n)!=EOF)
    {
        init();
        int m;
        scanf("%d",&m);
        for(int i=0; i<m; i++)
        {
            int cx,cy;
            scanf(" (%d %d)",&cx,&cy);
            vv[cx].push_back(cy);
            vv[cy].push_back(cx);
        }
        LCA(roott);

        for(int i=1; i<=n; i++)
        {
            if(ans[i]==0)
                continue;
            printf("%d:%d\n",i,ans[i]);
        }

    }


    return 0;
}