逻辑斯蒂回归

一：二元逻辑回归模型

二项逻辑斯蒂回归模型是如下的条件概率分布：

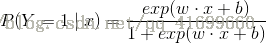
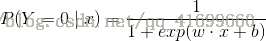
其中，Y为输出，w称为权值向量，b称为偏置。逻辑斯蒂回归比较两个条件概率值的大小，将实例x分到概率值较大的那一类。

一个事件的几率是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是p，那么该事件发生的几率是p/1-p

该事件的对数几率或logit函数是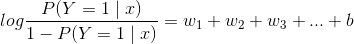

这就是说，在逻辑斯蒂回归模型中，输出Y=1的对数几率是输入x的线性函数。

二：多项逻辑斯蒂回归

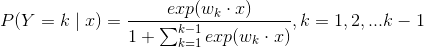
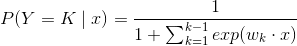
三：模型参数估计

设：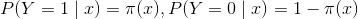

似然函数为  

对数似然函数为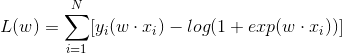 

对L(w）求极大值，得到w的估计值。这样，问题就变成了以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降法及拟牛顿法。

四：线性回归和逻辑斯蒂回归的联系

线性回归是回归问题，逻辑斯蒂回归是分类问题。线性回归通过最小二乘法确定参数，逻辑斯蒂回归通过最大似然估计确定参数。