x是n维实数空间,sign是符号函数,w和b为感知机模型参数,w叫作权值或者权值向量,b叫作偏置。
b.感知机模型的损失函数
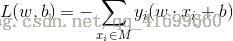
其中M为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。
显然,损失函数L(w,b)是非负的。如果没有误分类点,损失函数值是0
c.感知机模型损失函数的优化方法、以及什么是梯度下降法
感知机学习问题转化为求解损失函数的最优化问题。最优化的方法是随机梯度下降法。
首先,任意选取一个超平面,然后用梯度下降法不断地极小化目标函数。在极小化过程中不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。
假设误分类点集合M是固定的,那么损失函数L(w,b)的梯度由
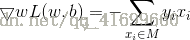
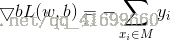
给出。
随机选取一个误分类点(Xi,Yi),对w,b进行更新:
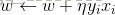
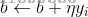
式中η(0<η≤1)是步长,在统计学习中又称为学习率。这样,通过迭代可以期待损失函数L(w,b)不断减小,直到为0.
d.感知机模型算法过程
输入:训练数据集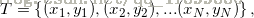 其中
其中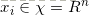 ,
, 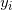 ={-1,+1},i=1,2,...N;学习率η(0<η≤1);
={-1,+1},i=1,2,...N;学习率η(0<η≤1);
输出:w,b;感知机模型
(1)选取初始值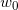 ,
,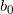
(2)在训练集中选取数据(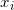 ,
,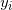 )
)
(3)如果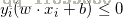
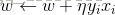
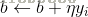
(4)转至2,直至训练集中没有误分类点。
e.感知机模型算法的对偶形式(过程)
输入:训练数据集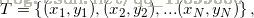 其中
其中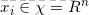 ,
,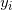 ={-1,+1},i=1,2,...N;学习率η(0<η≤1);
={-1,+1},i=1,2,...N;学习率η(0<η≤1);
输出: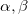 ;感知机模型
;感知机模型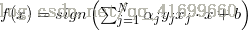 ,其中
,其中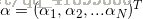
这里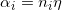
(1)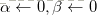
(2)在训练集中选取数据(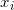 ,
,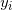 )
)
(3)如果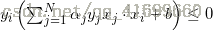
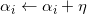

(4)转至(2)直到没有误分类数据。
对偶形式中训练实例仅以內积的形式出现。为了方便,可以预先将训练集中实例间的內积计算出来并以矩阵的形式存储,这个矩阵就是所谓的Gram矩阵
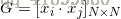







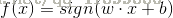
















 1484
1484

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








