量子遗传算法原理与MATLAB仿真程序

最新推荐文章于 2025-04-04 11:14:20 发布

子木呀

最新推荐文章于 2025-04-04 11:14:20 发布

阅读量4k

点赞数 14

文章标签： matlab 遗传算法量子遗传算法智能算法

本文链接：https://blog.youkuaiyun.com/qq_41687938/article/details/122723664

版权

写在前面：

1、其实这些智能算法的思想都差不多，只不过是各自搜寻方式、编码方式、种群更新方式等不一样而已。

量子遗传算法是在遗传算法的基础上使用了一种新的编码方式。

2、直接看前面介绍可能会觉得较难，先浏览概念任何根据案例走一遍就明白了。

3、遗传算法及其他智能算法：

遗传算法的简介与应用 - 知乎写在前面遗传算法是通过大量备选解的变换、迭代和变异，在解空间中并行动态地进行全局搜索的最优化方法．由于遗传算法具有比较完备的数学模型和理论，在解决很多NP—Hard问题上具有良好的性能． 1.因为我也是…https://zhuanlan.zhihu.com/p/49055485 智能优化算法——粒子群算法原理与仿真程序 - 知乎写在前面：粒子群算法很古老了，资料也很多，大部分寻优算法思想类似，本文稍作整理，并在文末分别附上C++、Python、MATLAB程序，如果本文对你有所帮助，请点赞支持一下！这是遗传算法的原理与程序：子木：遗传…https://zhuanlan.zhihu.com/p/460734234

4、如果本文对你有所帮助，请点赞支持一下！

原文链接：

量子遗传算法原理与MATLAB仿真程序 - 知乎写在前面：1、其实这些智能算法的思想都差不多，只不过是各自搜寻方式、编码方式、种群更新方式等不一样而已。量子遗传算法是在遗传算法的基础上使用了一种新的编码方式。 2、直接看前面介绍可能会觉得较难，先浏…https://zhuanlan.zhihu.com/p/462517360

一、量子遗传算法概述

量子遗传算法（quantum genetic algorithm,QGA）是量子计算与遗传算法相结合的产物，是一种新发展起来的概率进化算法。

遗传算法是处理复杂优化问题的一种方法，其基本思想是模拟生物进化的优胜劣汰规则与染色体的交换机制，通过选择、交叉、变异三种基本操作寻找最优个体。由于GA不受问题性质、优化准则形式等因素的限制，仅用目标函数在概率引导下进行全局自适应搜索，能够处理传统优化方法难以解决的复杂问题，具有极高鲁棒性和广泛适用性，因而得到了广泛应用并成为跨学科研究的热点。但是，若选择、交叉、变异的方式不当，GA会表现出迭代次数多、收敛速度慢、易陷入局部极值的现象。

量子计算中采用量子态作为基本的信息单元，利用量子态的叠加、纠缠和干涉等特性，通过量子并行计算可以解决经典计算中的NP问题。1994年Shor提出第一个量子算法，求解了大数质因子分解的经典计算难题，该算法可用于公开密钥系统RSA；1996年Grover 提出随机数据库搜索的量子算法，在量子计算机上可实现对未加整理的数据库 $\sqrt{N}$ 量级的加速搜索。量子计算正以其独特的计算性能迅速成为研究的热点。

量子遗传算法就是基于量子计算原理的一种遗传算法。将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，达到了比常规遗传算法更好的效果。

量子遗传算法建立在量子的态矢量表示的基础之上，将量子比特的几率幅表示应用于染色体的编码，使得一条染色体可以表达多个态的叠加，并利用量子逻辑门实现染色体的更新操作，从而实现了目标的优化求解。

二、量子染色体关键概念

2.1 量子比特编码

(该部分了解即可，看完全文再回来看即知为什么称为量子遗传算法)

在量子计算机中，充当信息存储单元的物理介质是一个双态量子系统，称为量子比特。量子比特与经典位不同就在于它可以同时处在两个量子态的叠加态中，比如：

$|\varphi\rangle=\alpha|0\rangle \beta|1\rangle$

$(\alpha,\beta)$ 是两个幅常数，满足

$|\alpha|^{2}+|\beta|^{2}=1$

其中， $|0\rangle$ 和 $|1\rangle$ 分别表示自旋向下和自旋向上态。所以一个量子比特可同时包含态 $|0\rangle$ 和 $|1\rangle$ 的信息。

在量子遗传算法中，采用量子比特存储和表达一个基因。该基因可以为“0”态或“1”态，或它们的任意叠加态。即该基因所表达的不再是某一确定的信息，而是包含所有可能的信息，对该基因的任一操作也会同时作用于所有可能的信息。

采用量子比特编码使得一个染色体可以同时表达多个态的叠加，使得量子遗传算法比经典遗传算法拥有更好的多样性特征。采用量子比特编码也可以获得较好的收敛性，随着 $|\alpha|^{2}$ 或 $|\beta|^{2}$ 趋于0或1，量子比特编码的染色体将收敛到一个单一态。

2.2 量子门更新

（量子遗传算法中的量子门更新的作用可理解为遗传算法中的变异或交叉操作）

量子门作为演化操作的执行机构，可根据具体问题进行选择，目前已有的量子门有很多种，根据量子遗传算法的计算特点，选择量子旋转门较为合适。量子旋转门的调整操作为：

$\boldsymbol{U}\left(\theta_{i}\right)=\left[\begin{array}{lr} \cos \left(\theta_{i}\right) & -\sin \left(\theta_{i}\right) \\ \sin \left(\theta_{i}\right) & \cos \left(\theta_{i}\right) \end{array}\right]$

其更新过程如下：

$\left[\begin{array}{c} \alpha_{i}^{\prime} \\ \beta_{i}^{\prime} \end{array}\right]=\boldsymbol{U}\left(\theta_{i}\right)\left[\begin{array}{c} \alpha_{i} \\ \beta_{i} \end{array}\right]=\left[\begin{array}{ll} \cos \left(\theta_{i}\right) & -\sin \left(\theta_{i}\right) \\ \sin \left(\theta_{i}\right) & \cos \left(\theta_{i}\right) \end{array}\right]\left[\begin{array}{l} \alpha_{i} \\ \beta_{i} \end{array}\right]$

其中， $\left(\alpha_{i}, \beta_{i}\right)^{\mathrm{T}}$ 和 $\left(\alpha_{i}^{\prime}, \beta_{i}^{\prime}\right)^{\mathrm{T}}$ 代表染色体第i个量子比特旋转门更新前后的概率幅； $\theta_{i}$ 为旋转角，它的大小和符号由事先设计的调整策略确定。

于是可以得出 $\alpha_{i}^{\prime}$ 和 $\beta_{i}^{\prime}$ 分别为：

$\left\{\begin{array}{l} \alpha_{i}^{\prime}=\alpha_{i} \cos \left(\theta_{i}\right)-\beta_{i} \sin \left(\theta_{i}\right) \\ \beta_{i}^{\prime}=\alpha_{i} \sin \left(\theta_{i}\right)+\beta_{i} \cos \left(\theta_{i}\right) \end{array}\right.$

所以

$\left|\alpha_{i}^{\prime}\right|^{2}+\left|\beta_{i}^{\prime}\right|^{2}=\left[\alpha_{i} \cos \left(\theta_{i}\right)-\beta \sin \left(\theta_{i}\right)\right]^{2}+\left[\alpha_{i} \sin \left(\theta_{i}\right)+\beta_{i} \cos \left(\theta_{i}\right)\right]^{2}=\left|\alpha_{i}\right|^{2}+\left|\beta_{i}\right|^{2}=1$

可以看出变换之后 $\left|\alpha_{i}^{\prime}\right|^{2}+\left|\beta_{i}^{\prime}\right|^{2}$ 的值仍为1。

三、量子遗传算法案例分析

3.1 问题描述

对于复杂二元函数求最值

$\max f(x, y)=x \sin (4 \pi x)+y \sin (20 \pi y)$

$\left\{\begin{array}{l} -3.0 \leqslant x\leqslant 12.1 \\ 4.1 \leqslant y \leqslant 5.8 \end{array}\right.$

该函数图像为：

二元函数图像

该图像程序为：

close all;clear;clc;
t1=-3:0.08:12.1;
t2=4.1:0.08:5.8;
x=t1;
y=t2;
[X,Y] = meshgrid(x,y);
Z=X.*sin(4.*pi.*X)+Y.*sin(20.*pi.*Y);
mesh(X,Y,Z);

从图可以看出，该非线性函数在给定范围内分布着许多局部极值，通常的寻优算法极易陷入局部极值或在各局部极值间振荡，比较适合于验证量子遗传算法的性能。

3.2 解题思路及步骤

1、量子遗传算法流程

量子遗传算法的流程如下：

（1）初始化种群 $Q\left(t_{0}\right)$ ，随机生成n个以量子比特为编码的染色体；

（2）对初始种群 $Q\left(t_{0}\right)$ 中的每个个体进行一次测量，得到对应的确定解 $P\left(t_{0}\right)$ ；

（3）对各确定解进行适应度评估；

（4）记录最优个体和对应的适应度；

（5）判断计算过程是否可以结束，若满足结束条件则退出，否则继续计算；

（6）对种群 $Q\left(t\right)$ 中的每个个体实施一次测量，得到相应的确定解；

（7）对各确定解进行适应度评估；

（8）利用量子旋转门 $U\left(t\right)$ 对个体实施调整，得到新的种群 $Q\left(t+1\right)$ ；

（9）记录最优个体和对应的适应度；

（10）将迭代次数t加1，返回步骤（5）。

对应的流程图如图所示。

量子遗传算法求解流程框图

算法步骤（1）是初始化种群 $Q\left(t_{0}\right)$ ，种群中全部染色体的所有基因 $\left(\alpha_{i}^{t}, \beta_{i}^{t}\right)$ 都被初始化为 $\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$ ，这意味着一个染色体所表达的是其全部可能状态的等概率叠加：

$\left|\psi_{q_{j}^{t}}\right\rangle=\sum_{k=1}^{2^{m}} \frac{1}{\sqrt{2}^{m}}\left|S_{k}\right\rangle$

其中， $S_{k}$ 为该染色体的第k种状态，表现形式为一长度为m的二进制串 $(x_{1}, x_{2},...,x_{m})$ , $x_{i}$ 的值为0或者1。

算法的步骤（2）是对初始种群中的个体进行一次测量，以获得一组确定的解 $P(t)=\{p_{1}^{t},p_{2}^{t},\cdot\cdot\cdot,p_{n}^{t}\}$ ，其中， $p_{j}^{t}$ 为第t代种群中第j个解（第j个个体的测量值），表现形式为长度为m的二进制串，其中每一位为0或1，是根据量子比特的概率（ $\left|\alpha_{i}^{t}\right|^{2}$ 或 $\left|\beta_{i}^{t}\right|^{2}$ ，i=1,2，…，m）选择得到的。测量过程为，随机产生一个[0,1]区间的数，若它大于概率幅的平方，则测量结果取值1，否则取值0。然后，对这一组解进行适应度评估，记录下最佳适应度个体作为下一步演化的目标值。

随后，算法进入循环迭代阶段，随着迭代的进行，种群的解逐渐向最优解收敛。在每一次迭代中，首先对种群进行测量，以获得一组确定解 $P\left(t\right)$ ，然后计算每个解的适应度值，再根据当前的演化目标和事先确定的调整策略，利用量子旋转门对种群中的个体进行调整，获得更新后的种群，记录下当前的最优解，并与当前的目标值进行比较，如果大于当前目标值，则以新的最优解作为下一次迭代的目标值，否则保持当前的目标值不变。

2、量子遗传算法实现

（1）量子比特编码

采用遗传算法中的二进制编码，对存在多态的问题进行量子比特编码，如两态用一个量子比特进行编码，四态用两个量子比特进行编码。该方法的优点是通用性好，且实现简单。采用多量子比特编码m个参数的基因如下：

$q_{j}^{t}=\left(\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c} \alpha_{11}^{t} & \alpha_{12}^{t} & \cdots & \alpha_{1 k}^{t} & \alpha_{21}^{t} & \alpha_{22}^{t} & \cdots & \alpha_{2 k}^{t} & \alpha_{m 1}^{t} & \alpha_{m 2}^{t} & \cdots & \alpha_{m k}^{t} \\ \beta_{11}^{t} & \beta_{12}^{t} & \cdots & \beta_{1 k}^{t} & \beta_{21}^{t} & \beta_{22}^{t} & \cdots & \beta_{2 k}^{t} & \beta_{m 1}^{t} & \beta_{m 2}^{t} & \cdots & \beta_{m k}^{t} \end{array}\right)$

其中， $q_{j}^{t}$ 代表第t代，第j个个体的染色体；k为编码每一个基因的量子比特数；m为染色体的基因个数。

将种群各个个体的量子比特编码 $(\alpha,\beta)$ 都初始化为 $\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$ ，这意味着一个染色体所表达的全部可能状态是等概率的。

（2）量子旋转门

量子遗传算法中，旋转门是最终实现演化操作的执行机构。这里使用一种通用的、与问题无关的调整策略，如表所示。

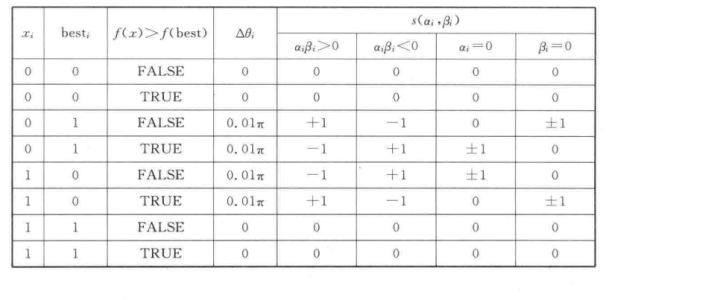
旋转角选择策略

其中， $x_i$ 为当前染色体的第i位； $best_i$ 为当前的最优染色体的第i位； $f(x)$ 为适应度函数； $s(\alpha_i,\beta_i)$ 为旋转角方向； $\Delta\theta_i$ 为旋转角度大小，其值根据表中所列的选择策略确定。该调整策略是将个体 $q_{j}^{t}$ 当前的测量值的适应度 $f(x)$ 与该种群当前最优个体的适应度值 $f(best_i)$ 进行比较，如果 $f(x)>f(best_i)$ ，则调整 $q_{j}^{t}$ 中相应位量子比特，使得几率幅对 $(\alpha_i,\beta_i)$ 向着有利于 $x_i$ 出现的方向演化；反之，如果 $f(x)<f(best_i)$ ，则调整 $q_{j}^{t}$ 中相应位量子比特，使得几率幅对 $(\alpha_i,\beta_i)$ 向着有利于 $best$ 出现的方向演化。

3.3 MATLAB程序实现

1、种群初始化

种群初始化函数为InitPop，其作用是产生初始种群的量子比特编码矩阵chrom。

function chrom=InitPop(M,N)
%% 初始化种群-量子比特编码
% M:为种群大小×2，(α和β)
% N:为量子比特编码长度
for i=1:M
    for j=1:N
        chrom(i,j)=1/sqrt(2);
    end
end

2、测量函数

对种群实施一次测量，得到二进制编码，函数名为collapse。

function binary=collapse(chrom)
%% 对种群实施一次测量 得到二进制编码
% 输入chrom ：为量子比特编码
% 输出binary：二进制编码
[M,N]=size(chrom);  %得到种群大小 和编码长度
M=M/2;  % 种群大小
binary=zeros(M,N);  %二进制编码大小初始化
for i=1:M
    for j=1:N
        pick=rand;  %产生【0,1】随机数
        if pick>(chrom(2.*i-1,j)^2)    % 随机数大于α的平方
            binary(i,j)=1;
        else
            binary(i,j)=0;
        end
    end
end

3、量子旋转门函数

旋转门是最终实现演化操作的执行机构，量子旋转门函数为Qgate，代码如下：

function chrom=Qgate(chrom,fitness,best,binary)
%% 量子旋转门调整策略
% 输入  chrom：更新前的量子比特编码
%     fitness：适应度值
%        best：当前种群中最优个体
%      binary：二进制编码
% 输出  chrom：更新后的量子比特编码
sizepop=size(chrom,1)/2;
lenchrom=size(binary,2);
for i=1:sizepop
    for j=1:lenchrom
        A=chrom(2*i-1,j);   % α
        B=chrom(2*i,j);     % β
        x=binary(i,j);
        b=best.binary(j);
        if ((x==0)&(b==0))||((x==1)&(b==1))
            delta=0;                  % delta为旋转角的大小
            s=0;                        % s为旋转角的符号，即旋转方向
        elseif (x==0)&(b==1)&(fitness(i)<best.fitness)
            delta=0.01*pi;
            if A*B>0
                s=1;
            elseif A*B<0
                s=-1;
            elseif A==0
                s=0;
            elseif B==0
                s=sign(randn);
            end
        elseif (x==0)&(b==1)&(fitness(i)>=best.fitness)
            delta=0.01*pi;
            if A*B>0
                s=-1;
            elseif A*B<0
                s=1;
            elseif A==0
                s=sign(randn);
            elseif B==0
                s=0;
            end
        elseif (x==1)&(b==0)&(fitness(i)<best.fitness)
            delta=0.01*pi;
            if A*B>0
                s=-1;
            elseif A*B<0
                s=1;
            elseif A==0
                s=sign(randn);
            elseif B==0
                s=0;
            end
        elseif (x==1)&(b==0)&(fitness(i)>=best.fitness)
            delta=0.01*pi;
            if A*B>0
                s=1;
            elseif A*B<0
                s=-1;
            elseif A==0
                s=0;
            elseif B==0
                s=sign(randn);
            end
        end
        e=s*delta;       % e为旋转角
        U=[cos(e) -sin(e);sin(e) cos(e)];      % 量子旋转门
        y=U*[A B]';        % y为更新后的量子位
        chrom(2*i-1,j)=y(1);
        chrom(2*i,j)=y(2);
    end
end

4、适应度函数

这里以求解最大值问题为例进行说明。如果是求解最小值问题，可以将之转变成求最大值问题（加个负号即可），目标值越大的个体，其适应度值也应该越大，所以可以直接将所优化的目标函数作为适应度函数。

适应度主函数FitnessFunction的代码如下：

function [fitness,X]=FitnessFunction(binary,lenchrom)
%% 适应度函数
% 输入  binary：二进制编码
%     lenchrom：各变量的二进制位数
% 输出 fitness：适应度
%            X：十进制数（待优化参数）
sizepop=size(binary,1);
fitness=zeros(1,sizepop);
num=size(lenchrom,2);
X=zeros(sizepop,num);
for i=1:sizepop
    [fitness(i),X(i,:)]=Objfunction(binary(i,:),lenchrom);         % 使用目标函数计算适应度
end

其中，函数Objfunction是待优化的目标函数，这里以前面提到的二元函数为例进行说明。函数Objfunction的代码：

function [Y,X]=Objfunction(x,lenchrom)
%% 目标函数
% 输入     x：二进制编码
%   lenchrom：各变量的二进制位数
% 输出     Y：目标值
%          X：十进制数
bound=[-3.0 12.1;4.1 5.8];   % 函数自变量的范围
%% 将binary数组转化成十进制数组
X=bin2decFun(x,lenchrom,bound);
%% 计算适应度-函数值
Y=sin(4*pi*X(1))*X(1)+sin(20*pi*X(2))*X(2);

其中，函数bin2decFun是将二进制编码转换成十进制数。

5、量子遗传算法主函数

量子遗传算法主函数代码如下：

clc;
clear all;
close all;
%----------------参数设置-----------------------
MAXGEN=200;                        % 最大遗传代数
sizepop=40;                        % 种群大小
lenchrom=[20 20];          % 每个变量的二进制长度
trace=zeros(1,MAXGEN);
%--------------------------------------------------------------------------      
best=struct('fitness',0,'X',[],'binary',[],'chrom',[]);   % 最佳个体 记录其适应度值、十进制值、二进制编码、量子比特编码
%% 初始化种群
chrom=InitPop(sizepop*2,sum(lenchrom));
%% 对种群实施一次测量 得到二进制编码
binary=collapse(chrom); 
%% 求种群个体的适应度值，和对应的十进制值
[fitness,X]=FitnessFunction(binary,lenchrom);         % 使用目标函数计算适应度
%% 记录最佳个体到best
[best.fitness bestindex]=max(fitness);     % 找出最大值
best.binary=binary(bestindex,:);
best.chrom=chrom([2*bestindex-1:2*bestindex],:);
best.X=X(bestindex,:);
trace(1)=best.fitness;
fprintf('%d\n',1)
%% 进化
for gen=2:MAXGEN
    fprintf('%d\n',gen)  %提示进化代数
    %% 对种群实施一次测量
    binary=collapse(chrom);
    %% 计算适应度
    [fitness,X]=FitnessFunction(binary,lenchrom);
    %% 量子旋转门
    chrom=Qgate(chrom,fitness,best,binary);
    [newbestfitness,newbestindex]=max(fitness);    % 找到最佳值
    % 记录最佳个体到best
    if newbestfitness>best.fitness
        best.fitness=newbestfitness;
        best.binary=binary(newbestindex,:);
        best.chrom=chrom([2*newbestindex-1:2*newbestindex],:);
        best.X=X(newbestindex,:);
    end
    trace(gen)=best.fitness;
end

%% 画进化曲线
plot(1:MAXGEN,trace);
title('进化过程');
xlabel('进化代数');
ylabel('每代的最佳适应度');

%% 显示优化结果
disp(['最优解X：',num2str(best.X)])
disp(['最大值Y:',num2str(best.fitness)]);

6、结果分析

输出优化结果：

最优解×：11.62555.72504

最大值Y：17.3503

量子遗传算法优化200代得到的进化过程如图所示。

量子遗传算法进化过程图

本例是针对前面所描述的案例进行编写，用户可以根据自己的实际问题修改函数Objfunction（待优化的问题也并不局限在函数优化，可以是一个复杂的运算过程），再简单修改下主函数中的相应变量设置即可。

四、量子遗传算法的拓展思路

前面使用的是未改进的量子遗传算法，该算法可以做一些改进：

（1）前面使用的是固定旋转角策略，可以根据进化进程动态调整量子门的旋转角大小。算法运行初期设置较大的旋转角，随着进化代数的增加逐渐减小旋转角。调整策略是对个体 $q_{j}^{t}$ 进行测量，评估其适应度 $f(x_j)^t$ ，与保留的最优个体的适应度值 $f(best)$ 进行比较，根据比较结果调整 $q_{j}^{t}$ 中相应位量子比特，使得 $(\alpha,\beta)$ 朝着有利于最优确定解的方向进化。

（2）加入量子交叉操作。量子遗传算法中最能体现个体结构信息的是其进化目标，即个体当前最优确定解以及对应的适应度值，因此，可以考虑互换个体的进化目标以实现个体间信息的互换，从而实现量子交叉的目的。其基本操作就是在个体之间暂时交换最优确定解和最优适应度值，个体接受交叉操作后，它的进化方向将受到其他个体的影响，从而获取新的进化信息。

（3）加入量子变异操作。量子变异的作用是轻微地打乱某个个体当前的进化方向，以防止该个体的进化陷入局部最优。量子变异通过操作染色体编码实现，互换量子比特概率幅 $(\alpha,\beta)$ 的值，可将个体的进化方向彻底反转。量子变异操作采用单点变异和多点变异相结合的方式，以增强种群中基因的多样性。

（4）加入量子灾变。当算法经历数代稳定后，最优个体保持稳定时，算法可能陷入了局部最优解，此时采取量子灾变操作，可使其摆脱局部最优解。具体方法是，将种群中部分个体施加大的扰动，重新随机生成部分个体。