目录
Day01
题目1
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。
class Solution {
public int search(int[] nums, int target) {
int low = 0;
int high = nums.length - 1;
while(low <= high)
{
int mid = low + ((high - low) >> 1);
if(nums[mid] > target){
high = mid - 1;
}else if(nums[mid] < target){
low = mid + 1;
}else{
return mid;
}
}
return -1;
}
};class Solution {
public:
int search(vector<int>& nums, int target)
{
int right=nums.size();
int left=-1;//请注意此种情况我们需要查找的区间是(left,right);
int mid= left + ((right - left) >> 1);//这样写是为了防止int型数据过大导致溢出
while(left+1<right) //当left=right-1时易知区间(left,right)为空,需要在此时跳出循环
{
if(nums[mid]==target) return mid;
else if(nums[mid]>target)//证明答案只可能存在于区间(left,mid)中
right=mid;//将要查找的区间改为(left,mid)
else left=mid;//证明答案只可能存在于区间(mid,right)中,将要查找的区间改为(mid,right)
mid=(right-left)/2+left;
}
return -1;
}
};总结:C++中string的size与length的区别
在C++的string类中,有两种函数:length和size。他们的作用都是返回字符串的长度
那么,问题来了,他们两者有什么区别?
为了钻研,我们要先找到他们两者的源代码
让我们先找到length的源代码
首先,我们随便定义一个字符串,并调用length
#include <iostream>
#include <string>
using namespace std;
int main(){
string s;
s.length();
return 0;
}
然后,重点来了!按住Ctrl,点击length,就会跳到C++的库文件(如果看不懂,就选中length,右键到实现)
我们就可以看到length的源代码
length() const _GLIBCXX_NOEXCEPT
{ return _M_rep()->_M_length; }
然后,按照同样的步骤找到size的源代码
size() const _GLIBCXX_NOEXCEPT
{ return _M_rep()->_M_length; }
可以看到两者的源代码一摸一样,所以这两者其实没有区别
但是为什么要搞两个呢?
其实string一开始只有length,这是C语言延续下来的习惯
而size则是在出现STL之后,为了兼容加入了和STL容器求长度的函数一个名字的size,这样就可以方便的使用于STL的算法
模板总结
用C++实现二分查找的算法:
模版三步走
1.设置判别函数check
2.根据check的结果来查看区间更新方式
3.查看区间更新方式来决定是否要+1
算法思路:
假设目标值在闭区间[l, r]中, 每次将区间长度缩小一半,当l = r时,我们就找到了目标值。
版本1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时,其更新操作是r = mid或者l = mid + 1;,计算mid时不需要加1。
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid;,此时为了防止死循环,计算mid时需要加1。
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}假设有一个总区间,经由我们的 check 函数判断后,可分成两部分,
这边以o作 true,.....作 false 示意较好识别
如果我们的目标是下面这个v,那麽就必须使用模板 1
................vooooooooo
假设经由 check 划分后,整个区间的属性与目标v如下,则我们必须使用模板 2
oooooooov...................
所以下次可以观察 check 属性再与模板1 or 2 互相搭配就不会写错啦
模板1和模板2本质上是根据代码来区分的,而不是应用场景。如果写完之后发现是l = mid,那么在计算mid时需要加上1,否则如果写完之后发现是r = mid,那么在计算mid时不能加1。
需不需要“+1”和check没关系,是根据check结束后所得的结果来判定到底是取上整还是取下整,如果取上整则该段程序都取上整,取下整则都取下整。其最终本质都是为了不重复的划分区间以二分找到最后的边界。详见链接
边界 [left, right] 的二分查找模板
int bSearch(vector<int>& arr, int target) {
int left = 0, right = arr.size() - 1;
while (left <= right) {
// 使用下面代码代替 (left + right) >> 1 防止相加后整型数据溢出
// >> 运算符的优先级比较小,要加括号
int mid = left + ((right - left) >> 1);
if (arr[mid] > target) {
right = mid - 1;
}else if (arr[mid] < target) {
left = mid + 1;
}else {
return mid;
}
}
return -1;
}
边界[left, right)的二分查找模板
注意边界条件,[left, right] 和 [left, right) 在处理 while(left <= right) 和 if (arr[mid] > target) 的时候代码有所不同。
模板返回的是找到满足某个条件下的数的下标,如果没找到返回 -1,可以根据题目适当做改变。
变体一:查找第一个值等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == 0) || (a[mid - 1] != value)) return mid;
else high = mid - 1;
}
}
return -1;
}变体二:查找最后一个值等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
else low = mid + 1;
}
}
return -1;
}重点还是第11行代码,如果 a[mid] 这个元素已经是数组中的最后一个元素了,那它肯定是我们要找的;如果或者后一个值不等于给定值,那也说明 a[mid] 就是我们要找的最后一个值等于给定值的元素。
如果我们经过检查之后,发现 a[mid] 后面的一个元素 a[mid+1] 也等于 value,那说明当前的这个 a[mid] 并不是最后一个值等于给定值的元素。我们就更新 low=mid+1,因为要找的元素肯定出现在 [mid+1, high] 之间。
变体三:查找第一个大于等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if ((mid == 0) || (a[mid - 1] < value)) return mid;
else high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}第10行,如果 a[mid] 小于要查找的值 value,那要查找的值肯定在 [mid+1, high] 之间,所以,我们更新 low=mid+1。
对于 a[mid] 大于等于给定值 value 的情况,我们要先看下这个 a[mid] 是不是我们要找的第一个值大于等于给定值的元素。如果 a[mid] 前面已经没有元素,或者前面一个元素小于要查找的值 value,那 a[mid] 就是我们要找的元素。这段逻辑对应的代码是第 7 行。
如果 a[mid-1] 也大于等于要查找的值 value,那说明要查找的元素在 [low, mid-1] 之间,所以,我们将 high 更新为 mid-1。
变体四:查找最后一个小于等于给定值的元素
查找最后一个小于等于给定值的元素。比如,数组中存储了这样一组数据:3,5,6,8,9,10。最后一个小于等于 7 的元素就是 6。是不是有点类似上面那一种?实际上,实现思路也是一样的。
有了前面的基础,你完全可以自己写出来了,所以我就不详细分析了。我把代码贴出来,你可以写完之后对比一下。
public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
else low = mid + 1;
}
}
return -1;
}我们还是重点看第 9 行代码。如果 a[mid] 这个元素已经是数组中的最后一个元素了,那它肯定是我们要找的;如果 a[mid] 的后一个元素 a[mid+1] 大于 value,那也说明 a[mid] 就是我们要找的最后一个值等于给定值的元素。
如果我们经过检查之后,发现 a[mid] 后面的一个元素 a[mid+1] 小于等于 value,那说明当前的这个 a[mid] 并不是最后一个值等于给定值的元素。我们就更新 low=mid+1,因为要找的元素肯定出现在 [mid+1, high] 之间。
练习
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n- 1;
while(left <= right) {
int mid = (left + right)/2;
if(nums[mid] > target) right = mid -1;
else if(nums[mid] < target) left = mid + 1;
else return mid;
}
return right + 1;
}
};题目2
暴力AC
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int size = nums.size();
for(int i = 0; i < size; i++)
{
if(nums[i] == val) {
for(int j = i + 1; j < size; j++){
nums[j - 1] = nums[j];
}
i--;
size--;
}
}
return size;
}
};双指针算法
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int j = 0;
for(int i = 0; i < nums.size(); i++){//i:fastIndex++
if(val != nums[i]){
nums[j++] = nums[i];//j:slowindex//第二个循环,遇到需要删除的元素,将后面的元素一个一个向前移动
}
}
return j;
}
};Day02
题目1 977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
暴力AC法
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
for (int i = 0; i < A.size(); i++) {
A[i] *= A[i];
}
sort(A.begin(), A.end()); // 快速排序
return A;
}
};双指针
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int k = nums.size() - 1;
vector<int> result(nums.size(), 0);
for(int i = 0, j = nums.size() - 1; i <= j; ){// 注意这里要i <= j,因为最后要处理两个元素
if(nums[i] * nums[i] < nums[j] * nums[j]){
result[k--] = nums[j] * nums[j];
j--;
}
else{
result[k--] = nums[i] * nums[i];
i++;
}
}
return result;
}
};题目2 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
滑动窗口
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0;//滑动窗口数值之和
int i = 0;//滑动窗口起始位置
int subLength = 0;//滑动窗口的长度
for(int j = 0; j < nums.size(); j++){
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while(sum >= target) {
subLength = (j - i + 1);//取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; //不断变更i(子序列的起始位置)
}
}
//如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};滑动窗口知识点:
题目3:59. 螺旋矩阵 II
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n , 0));//使用vector定义一个二维数组
int startx = 0, starty = 0;//定义每循环一个圈的起始位置
int loop = n / 2; //每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; //矩阵中间的位置,例如:n 为 3, 中间的位置就是(1,1),n为5,中间的位置为(2,2)
int count = 1;//用来给矩阵中每一个空格赋值
int offset = 1;//需要控制每一条边遍历的长度,每次循环右边界收缩一位;
int i, j;
while(loop --){
i = startx;
j = starty;
//下面开始的四个for就是模拟转了一圈
//模拟填充上行从左到右(左闭右开)
for(j = startx; j < n - offset; j++){
res[startx][j] = count++;
}
//模拟填充右列从上到下(左闭右开)
for(i = startx; i < n - offset; i++){
res[i][j] = count++;
}
//模拟填充下行从右到左(左闭右开)
for(; j > startx; j--){
res[i][j] = count++;
}
//模拟填充左列从下到上(左闭右开)
for( ; i > startx; i--){
res[i][j] = count++;
}
//第二圈开始的时候,起始位置要各自加一, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
startx++;
starty++;
//offset 控制每一圈里每一条边遍历的长度
offset += 1;
}
//如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if(n % 2 ){
res[mid][mid] = count;
}
return res;
}
};Day03
题目1:移除元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
ListNode* cur = dummyHead;
while (cur->next != NULL) {
if(cur->next->val == val) {
ListNode* tmp = cur->next;
cur->next = cur->next->next;
delete tmp;
} else {
cur = cur->next;
}
}
head = dummyHead->next;
delete dummyHead;
return head;
}
};设置一个虚拟头结点在进行移除节点操作:
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作
ListNode* cur = dummyHead;
while (cur->next != NULL) {
if(cur->next->val == val) {
ListNode* tmp = cur->next;
cur->next = cur->next->next;
delete tmp;
} else {
cur = cur->next;
}
}
head = dummyHead->next;
delete dummyHead;
return head;
}
};题目2:设计链表
class MyLinkedList {
public:
//定义链表节点结构体
struct LinkedNode{
int val;
LinkedNode* next;
LinkedNode(int val): val(val), next(nullptr){}
};
//初始化链表
MyLinkedList() {
_dummyHead = new LinkedNode(0);//这里定义的头结点 是一个虚拟的头结点。而不是真正的链表的头结点
_size = 0;
}
//获取到第index个节点数值,如果index是非法数值直接返回-1,注意index是从0开始的,第0个节点就是头结点
int get(int index) {
if(index > (_size - 1) || index < 0){
return -1;
}
LinkedNode* cur = _dummyHead -> next;
while (index){//如果--index 就会陷入死循环 c++的while(n)就是while(n>0)
cur = cur -> next;
index--; //更方便的写法: while(index--){}
}
return cur -> val;
}
//在链表最前面插入一个节点。插入完成后,新插入的节点为链表的新的头结点
void addAtHead(int val) {
LinkedNode* newNode = new LinkedNode(val);//定义新的链表节点
newNode->next = _dummyHead->next;//顺序不能变
_dummyHead->next = newNode;
_size++;
}
//在链表最后面添加一个节点
void addAtTail(int val) {
LinkedNode* newNode = new LinkedNode(val);//默认指向null
LinkedNode* cur = _dummyHead;
while(cur->next != nullptr){//cur->next 不为空,执行遍历,直到找到cur->next为空为止,说明cur临时指针指向尾部节点
cur = cur -> next;
}
cur->next = newNode;
_size++;
}
//在第index个节点之前插入一个新节点,例如index= 0,那么新插入的节点为链表的新头结点,既要知道第n个节点,又要知道第n - 1个节点
//如果index等于链表的长度,则说明是新插入的节点为链表的尾结点
//如果index大于链表的长度,则返回空
void addAtIndex(int index, int val) {
if(index > _size){
return;
}
LinkedNode* newNode = new LinkedNode(val);
LinkedNode* cur = _dummyHead;
while(index--){
cur = cur->next;
}
newNode->next = cur->next;//顺序不能变
cur->next = newNode;
_size++;
}
//删除第index个节点,如果index大于等于链表的长度,直接return,注意index是从0开始的
void deleteAtIndex(int index) {
if(index >= _size || index < 0) {//①合法性判断
return;
}
LinkedNode* cur = _dummyHead;//②创建虚拟结点 第index个节点一定时cur->next,操作cur,来删除cur->next
while(index--){//③遍历。去找第n个节点
cur = cur->next;//设想极端条件处理边界问题(只有一个个节点)
}
LinkedNode* tmp = cur -> next;//c++里面需要对内存进行及时释放
cur -> next = cur -> next -> next;//④删除操作
delete tmp;//c++里面需要对内存进行及时释放
_size--;
}
private:
int _size;
LinkedNode* _dummyHead;
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* MyLinkedList* obj = new MyLinkedList();
* int param_1 = obj->get(index);
* obj->addAtHead(val);
* obj->addAtTail(val);
* obj->addAtIndex(index,val);
* obj->deleteAtIndex(index);
*/题目3 反转链表
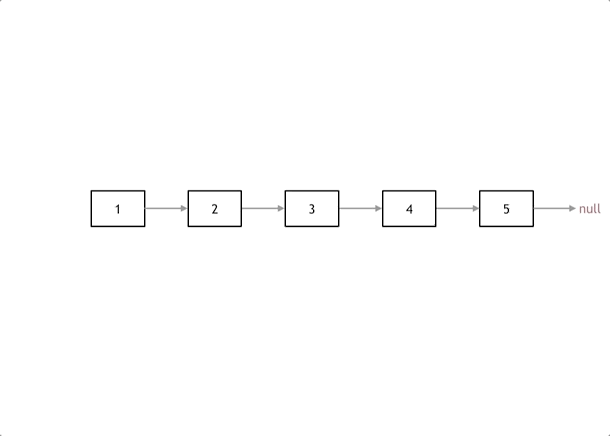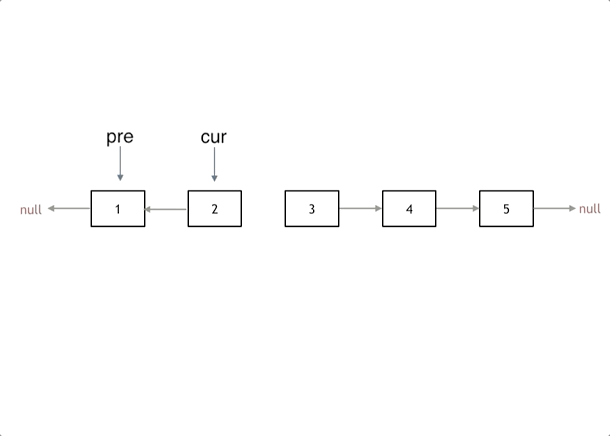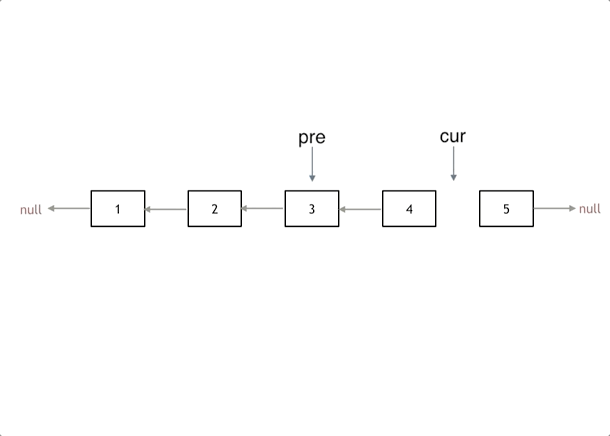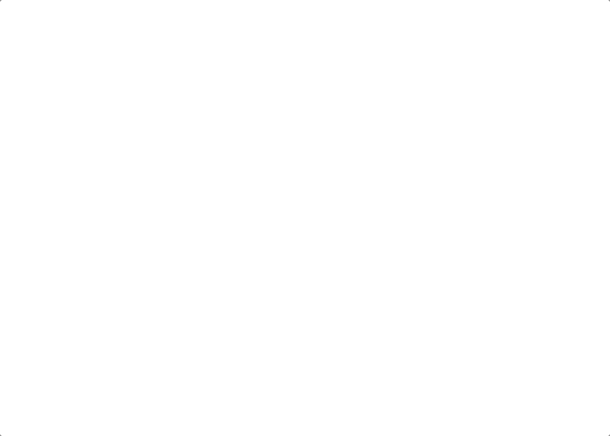
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* temp; //保存cur的下一个节点,因为接下来要改变cur->next
ListNode* cur = head;
ListNode* pre = NULL;
while(cur){
temp = cur->next;
cur->next = pre;//翻转操作
//更新pre 和 cur指针
pre = cur;
cur = temp;
}
return pre;
}
};
//1. temp 保存临时变量
//2. change 改变链表
//3. next 迭代当前指向 Day04
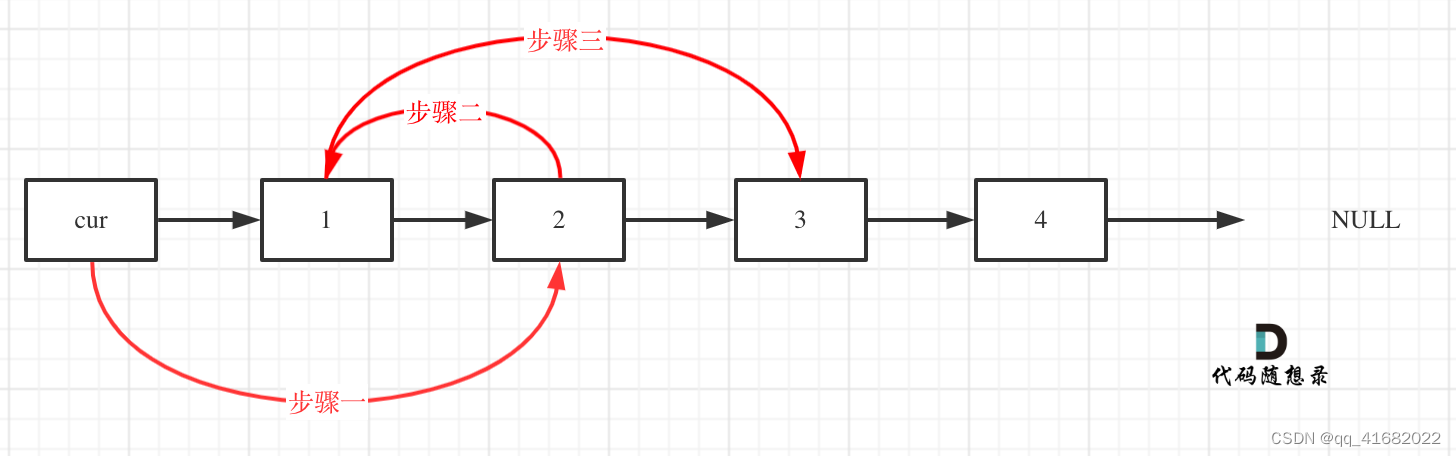
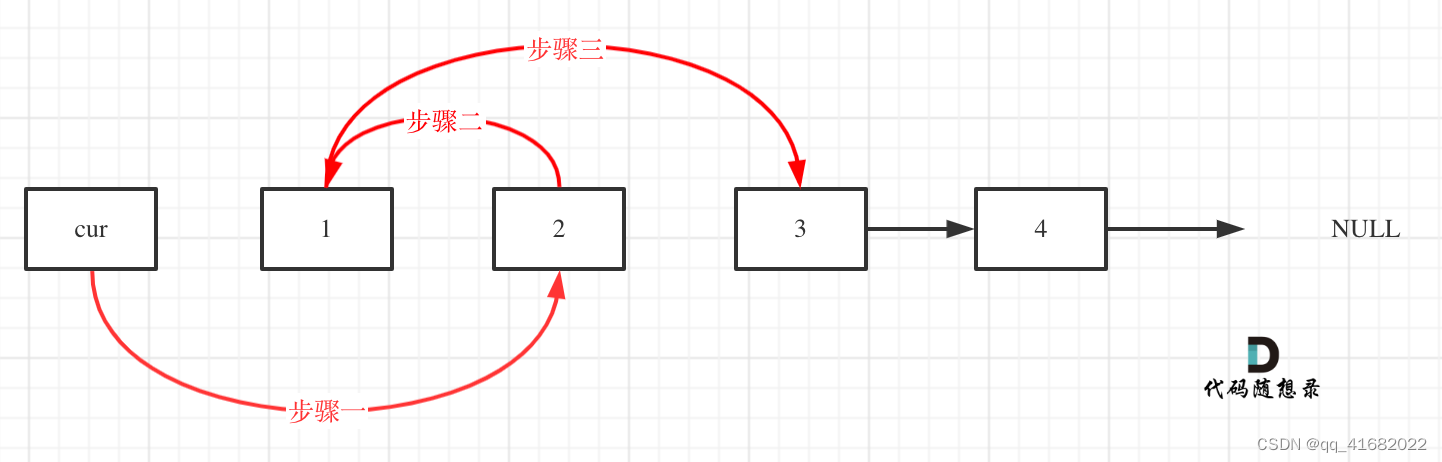
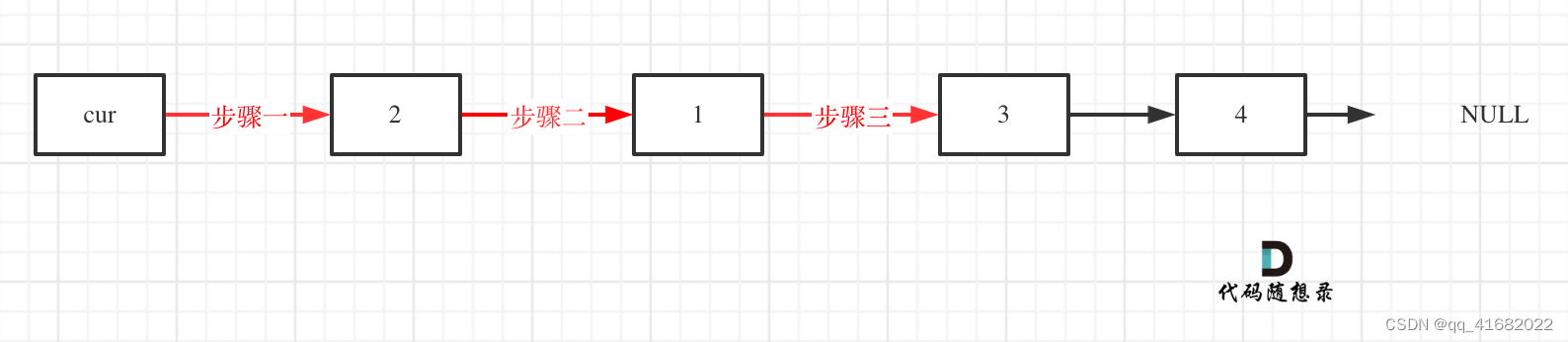
题目1 24. 两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
链表合集:疑问:ListNode结构体 怎么用的
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);//设置一个虚拟头结点;
dummyHead->next = head;//将虚拟头结点指向head,这样方便后面做删除操作;
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr){
ListNode* tmp = cur->next;//记录临时节点
ListNode* tmp1 = cur->next->next->next;//记录临时节点
cur->next = cur->next->next;//步骤一
cur->next->next = tmp;//步骤二
cur->next->next->next = tmp1;//步骤三
cur = cur -> next -> next;// cur移动两位,准备下一轮交换
}
return dummyHead->next;
}
};java null
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if(head == null || head.next == null){//终止条件:本题终止条件很明显,当递归到链表为空或者链表只剩一个元素时,没得交换了。自然终止。
return head;
}
ListNode next = head.next;//现在有一个ListNode 它指向head的后面一个节点
head.next = swapPairs(next.next);
next.next = head;//单次的过程,因为递归是重复做一样的事情,所以从宏观上考虑,只用考虑某一步是怎么完成的。我们假设待交换的两个节点分别为head和next,next的应该接受上一级返回的子链表。就相当于是一个含三个节点的链表交换前两个节点。
return next;//找返回值,返回给上一层递归的值应该是已经交换完成后的子链表;
}
}C++ NULL
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(head == NULL || head->next == NULL){//终止条件:本题终止条件很明显,当递归到链表为空或者链表只剩一个元素时,没得交换了。自然终止。
return head;
}
ListNode* next = head->next;
head->next = swapPairs(next->next);
next->next = head;//单次的过程,因为递归是重复做一样的事情,所以从宏观上考虑,只用考虑某一步是怎么完成的。我们假设待交换的两个节点分别为head和next,next的应该接受上一级返回的子链表。就相当于是一个含三个节点的链表交换前两个节点。
return next;//找返回值,返回给上一层递归的值应该是已经交换完成后的子链表;
}
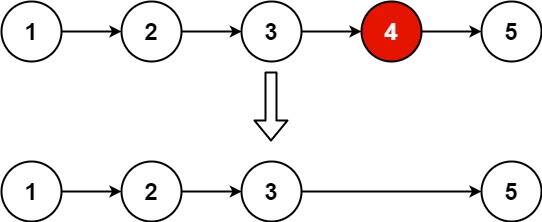
};题目2 19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* slow = dummyHead;
ListNode* fast = dummyHead;//快慢指针
while(n-- && fast != NULL){
fast = fast -> next;
}
fast = fast -> next;
while(fast != NULL){
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;//删除操作
return dummyHead->next;
}
};面试题 02.07. 链表相交
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA;
ListNode* curB = headB;
int lenA = 0, lenB = 0;//初始化
while(curA != NULL){//求链表A长度
lenA++;
curA = curA -> next;
}
while(curB != NULL){//求链表B长度
lenB++;
curB = curB -> next;
}
curA = headA;
curB = headB;
//让curA为最长链表的头,lenA为其长度
if(lenB > lenA){
swap(lenA,lenB);
swap(curA,curB);
}
//求长度差
int gap = lenA - lenB;
//让curA和curB在同一起点上
while(gap--){
curA = curA->next;
}
//遍历curA 和 curB 遇到相同则直接返回
while(curA != NULL){
if(curA == curB){
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};142.环形链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA;
ListNode* curB = headB;
int lenA = 0, lenB = 0;//初始化
while(curA != NULL){//求链表A长度
lenA++;
curA = curA -> next;
}
while(curB != NULL){//求链表B长度
lenB++;
curB = curB -> next;
}
curA = headA;
curB = headB;
//让curA为最长链表的头,lenA为其长度
if(lenB > lenA){
swap(lenA,lenB);
swap(curA,curB);
}
//求长度差
int gap = lenA - lenB;
//让curA和curB在同一起点上
while(gap--){
curA = curA->next;
}
//遍历curA 和 curB 遇到相同则直接返回
while(curA != NULL){
if(curA == curB){
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};Day6 哈希表
242. 有效的字母异位词
class Solution {
public:
bool isAnagram(string s, string t) {
int hash[26] = {0};
for(int i = 0; i < s.size(); i++){
//并不需要记住字符a的ASCII,只要求出一个相对数值就可以了
hash[s[i] - 'a']++;
}
for(int i = 0; i < t.size(); i++){
hash[t[i] - 'a']--;
}
for(int i = 0; i < 26; i++){
if(hash[i] != 0){
//hash数组如果有元素不为0,说明字符串s和t 一定是谁多了字符或者谁少了字符。
return false;
}
}
return true;
}
};349.两个数组的交集
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set;//存放结果,之所以使用unordered_set是为了给结果集去重,而不是使用muti_set,这个去重不了
unordered_set<int> nums_set(nums1.begin(), nums1.end());//使用迭代器,1.begin迭代器:指向第一个元素的位置; 2.end迭代器:指向最后一个元素的末尾;生成指向容器中第一个元素和尾元素之后位置的迭代器。
for(int num : nums2){//foreach的遍历,遍历nums2数组中的每一个成员,num:表示你每遍历集合中一个元素 便存储到该变量中.
// 发现nums2的元素 在nums_set里又出现过
if(nums_set.find(num) != nums_set.end()){
result_set.insert(num);
}
}
return vector<int>(result_set.begin(),result_set.end());
}
};202.快乐数
class Solution {
public:
//取数值各个位上的单数之和
int getSum(int n){
int sum = 0;//初始化
while(n){
sum += (n % 10) * (n % 10);//q取余操作,个位平方
n /= 10;//十位、百位...
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> set;
while(1){//1:条件为真时循环,如果是0则表示条件为假时循环。
int sum = getSum(n);
if(sum == 1){
return true;
}
//如果这个sum曾经出现过,说明已经陷入了无限循环,离开return false;
if(set.find(sum) != set.end()){
return false;
}else{
set.insert(sum);
}
n = sum;
}
}
};1.两数之和
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
std:unordered_map <int, int> map;//<key类型, value类型>
for(int i = 0; i < nums.size(); i++){
//遍历当前元素,并在map中寻找是否有匹配的key
auto iter = map.find(target - nums[i]);
if(iter != map.end()){
return {iter -> second, i};//找到的元素下标 和 当前遍历的元素
}
//如果没有找到匹配对,就把访问过的元素和下标加入到map中;
map.insert(pair<int, int>(nums[i], i));
}
return {};//遍历结束还没找到,return 一个空的集合就行
}
};



 这是一个关于代码随想录训练营的博客,内容涵盖算法练习,主要涉及LeetCode上的问题,如二分查找、链表操作等。博主分享了不同链表问题的解决方案,包括移除元素、设计链表、反转链表等,并探讨了哈希表在解决实际问题中的应用,如查找字母异位词、求两个数组的交集和两数之和。
这是一个关于代码随想录训练营的博客,内容涵盖算法练习,主要涉及LeetCode上的问题,如二分查找、链表操作等。博主分享了不同链表问题的解决方案,包括移除元素、设计链表、反转链表等,并探讨了哈希表在解决实际问题中的应用,如查找字母异位词、求两个数组的交集和两数之和。
 https://code-thinking.cdn.bcebos.com/gifs/977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.gif
https://code-thinking.cdn.bcebos.com/gifs/977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.gif















 1162
1162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








