回溯法 n皇后问题

1 描述

nxn棋盘放n个皇后，要求批次不能攻击
同行、同列or同一斜线上不能放两个皇后
求总共有几种放置方案

2 分析

1. 对于一个按照要求放入的棋子，他所在的行 i ，列 i’, 都被他占据，还有他的斜线，那么在放置下一个棋子的时候，如果有j==i（不能同行）；j’==i’（不能同列），或者是 |i’-i|==|j’-j|（不能在一个斜线上），那么这个和j对应的位置就不能放置，需要寻找下一个位置。

2. 算法思想（回溯）
   backtrace(t)
   1). 若t>n,得到一个完整的放置方案，记录返回
   2). 对于i=：n
   3). | x[t]=i, //在第t行第x[t]列放一个皇后
   4). | 若place(t), 则backtrack(t+1) //约束条件，就是第1步的分析
   <1>. place(t): 确定(t,x[t])与(i,x[i])无冲突(1<=i<=t-1),
   5). backtrace(t+1)

3. 每一层递归就是在放置一个皇后，相当于每一层递归都是在寻找在这一层列的方向上有几种放置方式，所以不用考虑行的影响，
   考虑斜线是列方向的差值是正数，但是行方向上的差值可能是正，也可能是负，所以加上绝对值号

3 代码

//代码考虑的是8个皇后的情况
#include <cstring>
#include <iostream>
#include <math.h>
using namespace std;

int  n, tot;
int  C[8];  //第i个皇后放置在了c[i]列，也就是说它的位置是  （i，c[i]）
void backtrace(int level)
{
    if(level == n)
        tot++;  // 递归边界. 只要走到这里,所有皇后必然不冲突
    else
        for(int i = 0; i < n; i++) {  //对于这一行的每一个位置都要检查是否符合条件
            int ok = 1;
            for(int j = 0; j < level; j++)  // 对已经放置的0~level-1行验证
            {  // 验证列:第j行的列是否等于第level行的列
                // 验证对角线: 行-列的差是否相等
                if(i == C[j] || level - j == abs(i - C[j])) {  // 再验证放的位置是否符合要求
                    ok = 0;
                    break;  //只要属于其中一个皇后的势力范围，这个点不能放，直接返回找下一个点
                }
            }
            if(ok) {
                C[level] = i;  // 第level行的皇后放在第i列
                backtrace(level + 1);
            }
        }
}

int main()
{
    n   = 8;
    tot = 0;
    backtrace(0);
    printf("sum: %d\n", tot);
    return 0;
}

结果：

4 补充

之前在看到有另一种解法，算法是一样的，但是在判断某个位置是否能放置的时候有差异，刚开始一直没看懂，后来明白了
先贴代码

#include <iostream>
using namespace std;
#define N 8
int  column[N + 1];  // 同栏是否有皇后，1表示有
int  rup[2 * N + 1];  // 右上至左下是否有皇后
int  lup[2 * N + 1];  // 左上至右下是否有皇后
int  queen[N + 1] = {0};
int  num;  // 解答编号
void backtrack(int);  // 递归求解
int  main(void)
{
    int i;
    num = 0;
    for(i = 1; i <= N; i++)
        column[i] = 1;
    for(i = 1; i <= 2 * N; i++)
        rup[i] = lup[i] = 1;
    backtrack(1);
    cout << endl
         << N << "个皇后在棋盘上总共有" << num << "种排法" << endl;
    return 0;
}

void backtrack(int i)
{
    int j;
    if(i > N) {
        num++;
        return;
    }
    else {
        for(j = 1; j <= N; j++) {
            if(column[j] == 1 && rup[i + j] == 1 && lup[i - j + N + 1] == 1) {
                queen[i] = j;
                // 设定为占用
                column[j] = rup[i + j] = lup[i - j + N + 1] = 0;
                backtrack(i + 1);
                column[j] = rup[i + j] = lup[i - j + N + 1] = 1;
            }
        }
    }
}

对于其中的这一行

 if(column[j] == 1 && rup[i + j] == 1 && lup[i - j + N + 1] == 1) 

为什么能实现判断的效果，占位信息是怎么存在数组中的
想了好久应该是给斜线进行了编号

1. rup这个数组

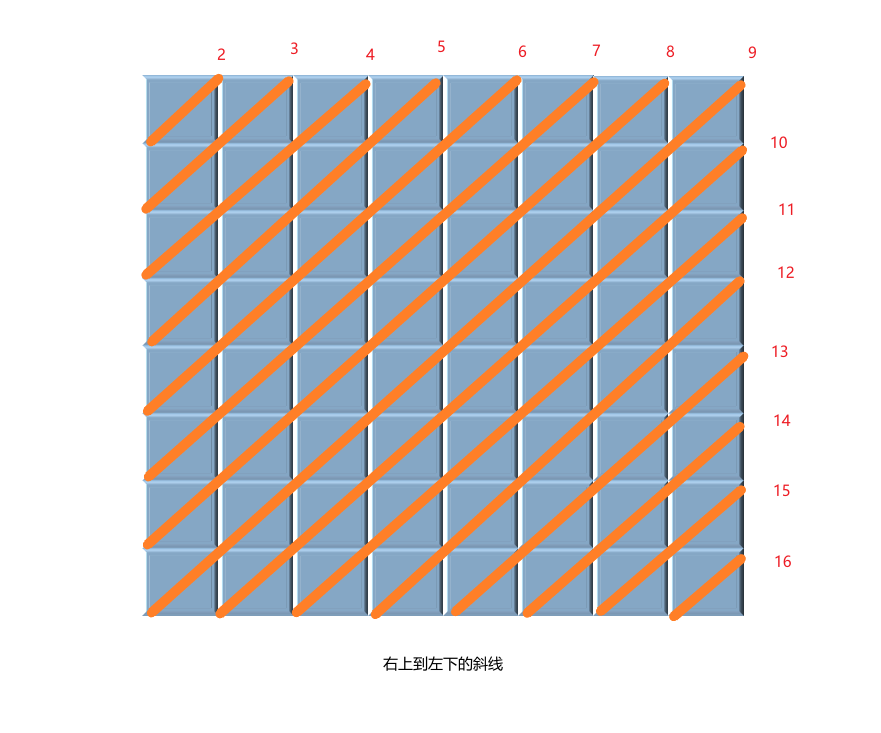
这样就对应上了，下标从2开始是因为1+1为2，最小就是2
比如说第2行第3列的格子对应的斜线就是rup[2+3]；

2. lup这个数组也是一样

这样所有的斜线就遍布了每一个格子
后面这个其实可以从1开始编号的，但是为了统一我就都从2开始了，带来的后果是增加了一步基础操作，每一次判断都多了一个**-1**操作