杭电ACM学习笔记（2）-----1005&1006

最新推荐文章于 2024-08-07 14:16:33 发布

原创最新推荐文章于 2024-08-07 14:16:33 发布 · 238 阅读

0 ·

CC 4.0 BY-SA版权

杭电ACM 专栏收录该内容

2 篇文章

订阅专栏

这篇博客探讨了杭电ACM竞赛中的两道题目1005和1006。博主提出利用递归思路转化为数组计算的方法，避免时间限制，同时发现结果存在周期性，c[n]==c[n%49]。尽管通过精度处理，模拟解法仍可能超时。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

//Author:ZJQ
//find repeated position
#include <stdio.h>
#include <stdlib.h>
int main()
{
    int a,b,n,i;
    int c[100];
    c[1]=1;
    c[2]=1;
    while(~scanf("%d %d %d",&a,&b,&n)&&(a!=0&&b!=0&&n!=0))
    {
        printf("1 %d\n",c[1]);
        printf("2 %d\n",c[2]);
        for(i=3;i<=n;i++)
        {
            c[i]=(a*c[i-1]+b*c[i-2])%7;
            printf("%d %d\n",i,c[i]);
        }
    }
}

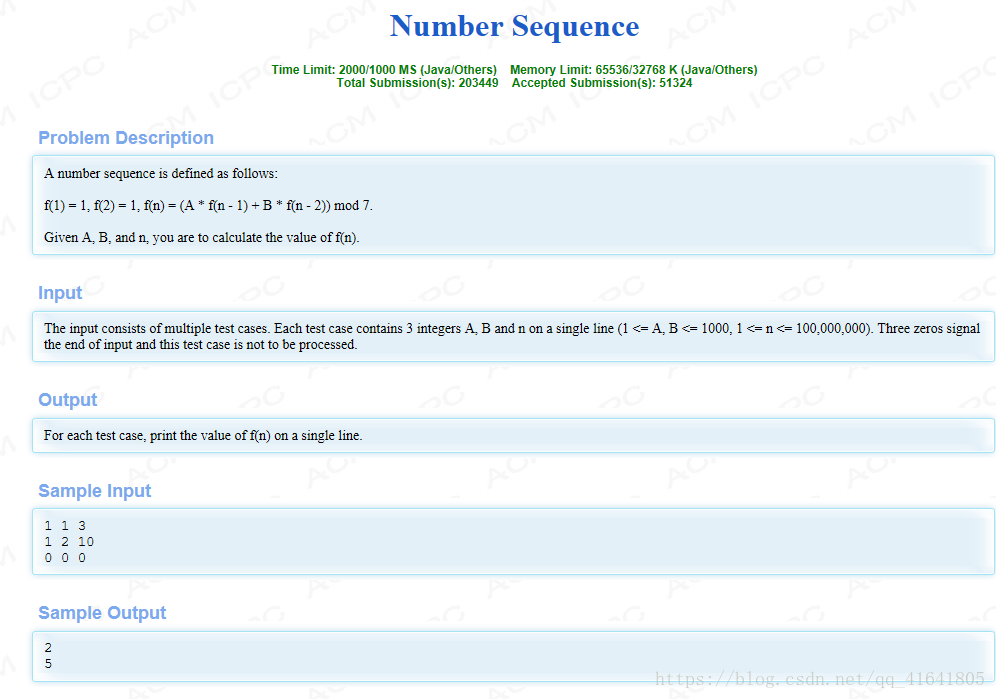
该题显然具有递归的思路，可以考虑将不同输入对应不同的函数结果转换成数组形式，数组每个位置存放对应的结果，计算时即可省去递归，直接从数组中取出相关值进行运算即可。（用空间换时间！）

但是如果暴力运算，会出现Time Limited，所以应尽量找出规律，即找出从第几个开始结果出现重复以简化代码。

上面的代码可以用来找到重复位置，发现：c[n]==c[n%49]！！

下面贴出简化后的代码：

//Author:ZJQ
#include <stdio.h>
#include <stdlib.h>
int main()
{
    int a,b,n,i;
    int c[100];
    c[1]=1;
    c[2]=1;
    while(~scanf("%d %d %d",&a,&b,&n)&&(a!=0&&b!=0&&n!=0))
    {
        for(i=3;i<=49;i++)
        {
            c[i]=(a*c[i-1]+b*c[i-2])%7;
        }
        printf("%d\n",c[n%49]);
    }
}

//Author:ZJQ
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
    int d,i;
    double dm,df,ds;
    int t;
    while(~scanf("%d",&d)&&d!=-1)
    {
        t=0;
        for(i=1;i<=3600*12*11;i++)//提高精度*11
        {
            dm=(360.0*i)/(60.0*11);
            df=(360.0*i)/(3600.0*11);
            ds=(360.0*i)/(3600*12.0*11);
            int n1=(int)(dm/360.0);
            int n2=(int)(df/360.0);
            int n3=(int)(ds/360.0);
            double hh1=fabs((dm-n1*360.0)-(df-n2*360.0));
            double hh2=fabs((dm-n1*360.0)-(ds-n3*360.0));
            double hh3=fabs((df-n2*360.0)-(ds-n3*360.0));
            if(hh1>180)
                hh1=360.0-hh1;
            if(hh2>180)
                hh2=360.0-hh2;
            if(hh3>180)
                hh3=360.0-hh3;
            if(hh1>=d&&hh2>=d&&hh3>=d)
            {
                t+=1;
            }
        }
        printf("%.3lf\n",t*100/(3600*12.0*11));
    }
}

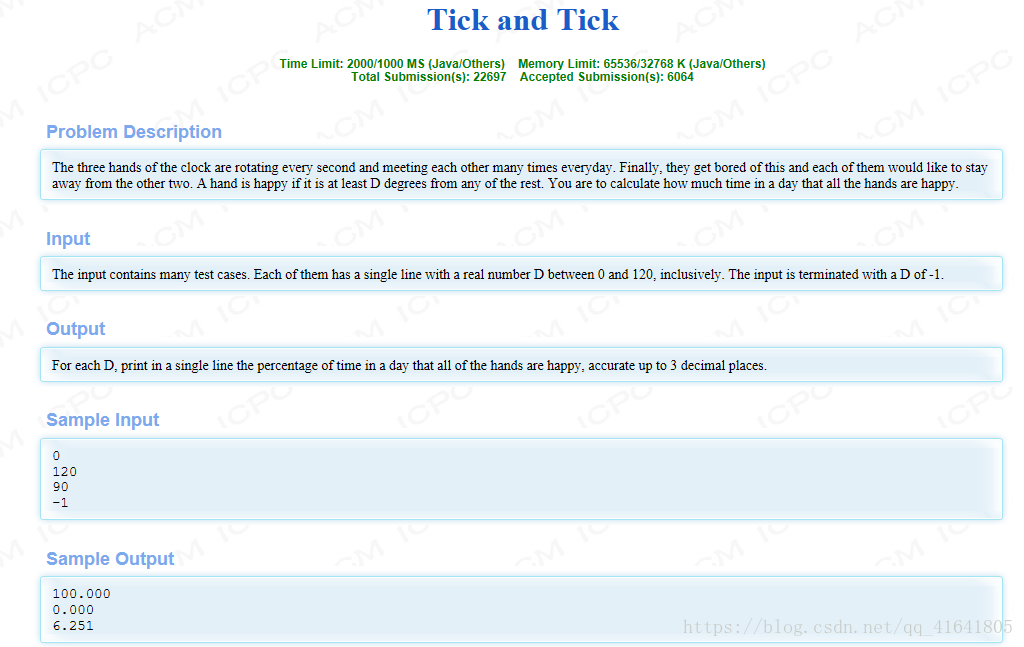
该题简直是100%纯天然的数学题，若用模拟，要不精度出问题，要不Time Limited，但个人认为本题实在无需过于纠结唯一的答案，故列出的代码依然是模拟，不过作了精度处理，使得答案一样，但还是超出时间。