本文深入解析scipy.optimize.fminbound函数的工作原理，包括参数分析、Brent方法及抛物线内插法的应用，并提供了从Python到C语言的移植示例。
为什么要做这个分析？
我试图用c语言翻译scipy.signal中的iirfilter函数，其中用到了fminbound。当使用我自定义的求极小值函数时，得到的传递函数系数值在小数点后四到五位有误差，但是得到的滤波器幅频响应差别很大，很不理想。强行翻译fminbound后无法正确输出。因此还是决定先理解，再编程。可把宝宝为难坏了。
scipy.optimize.fminbound官方说明
参考书：《C++数值算法》普雷斯著
scipy.optimize.fminbound
参数分析
def fminbound(func, x1, x2, args=(), xtol=1e-5, maxfun=500,
full_output=0, disp=1):
options = {'xatol': xtol,
'maxiter': maxfun,
'disp': disp}
res = _minimize_scalar_bounded(func, (x1, x2), args, **options)
if full_output:
return res['x'], res['fun'], res['status'], res['nfev']
else:
return res['x']
Parameters
-
func: callable f(x, *args)
Objective function to be minimized (must accept and return scalars).
欲取极小值的目标函数（必须接受并返回标量） -
x1, x2: float or array scalar
The optimization bounds.
取极小值的区间 -
args: tuple, optional
Extra arguments passed to functions.
目标函数的其他输入参数 -
xtop: float, optional
The convergence tolerance.
收敛容差，我理解是一个很小的常量 -
maxfun: int, optional
Maximum number of function evaluations allowed.
最大循环次数，如果在此次数之间没有得到极小值则跳出循环 -
full_output: bool, optional
If true, return optional outputs. -
disp: int, optional
If non-zero, print messages.
0: no message printing.
1: non-convergence notification messages only.
2: print a message on convergence too.
3: print iteration results.
Returns
-
xopt: ndarray
Parameters (over given interval) which minimize the objective function.
res[‘x’] 输出极小值的x值 -
fval: number
The function value at the minimum point
res[‘fun’] 极小值的y值 -
ierr: int
An error flag (0 if converged, 1 if maximum number of function calls reached).
res[‘status’] -
numfunc: int
The number of function calls made.
res[‘nfev’]
_minimize_scalar_bounded
这个函数非常长，因此我决定分步进行。
def _minimize_scalar_bounded(func, bounds, args=(),
xatol=1e-5, maxiter=500, disp=0,
**unknown_options):
Parameters
-
maxiter : int
Maximum number of iterations to perform.
最大迭代次数 -
disp: int, optional
If non-zero, print messages.
0 : no message printing.
1 : non-convergence notification messages only.
2 : print a message on convergence too.
3 : print iteration results. -
xatol : float
Absolute error in solutionxoptacceptable for convergence.
循环外
循环外定义以下参数：
常数
- xatol = 1e-5 # 收敛容差，为恰巧为0的极小值情况而设置的一个相对精确的小数
- maxfun = maxfun = 500 # 最大迭代次数
- sqrt_eps = sqrt(2.2e-16) # eps的开方，机器浮点精度的平方根，返回值的相对精度
- golden_mean = 0.5 * (3.0 - sqrt(5.0)) # 黄金分割点
变量
储存x与y值的变量
- fulc, nfc, xf, x # 储存x
- ffulc, fnfc, fx, fu # 储存y
其他变量
- a, b # 取值区间
- num # 迭代次数
- fmin_data = (1, x, y) # 储存当前迭代的次数以及x, y值
- flag = 0 # 状态判定
- xm = 0.5 * (a + b) # 当前范围的中点
- rat = e = 0.0 # 步长？
- tol1, tol2 # 判别值，其中tol1中唯一的变量为xf
循环内分析
Brent方法：x, y, a, b
# 用某种方式更新x, fu
x = xf + si * np.maximum(np.abs(rat), tol1)
fu = func(x, *args)
num += 1 # 更新迭代次数
fmin_data = (num, x, fu) # 储存当前值
if disp > 2:
print("%5.0f %12.6g %12.6g %s" % (fmin_data + (step,)))
# 以下为x, y, a, b的更新
if fu <= fx: # 条件 1
if x >= xf: # 条件 1-1
a = xf
else: # 条件 1-2
b = xf
fulc, ffulc = nfc, fnfc
nfc, fnfc = xf, fx
xf, fx = x, fu
else: # 条件 2
if x < xf: # 条件 2-1
a = x
else: # 条件 2-2
b = x
if (fu <= fnfc) or (nfc == xf): # 条件 2-1-1 或 2-2-1
fulc, ffulc = nfc, fnfc
nfc, fnfc = x, fu
elif (fu <= ffulc) or (fulc == xf) or (fulc == nfc): # 条件 2-1-2 或 2-2-2
fulc, ffulc = x, fu
-
开始循环之前：
- 设(x0, y0), [a0, b0]。有：
代表x的值：
fulc = nfc = xf = x = x0
代表y的值：
ffulc = fnfc = fx = y0
fu = np.inf
- 设(x0, y0), [a0, b0]。有：
-
第一次循环：
- 生成新的(x, fu) → (x1, y1)
- 更新：若满足条件 1-1:
fu <= fx & x < xf 函数下降
a1 = xf = x0, b1 = b0 (a1, b1) → (x0, b0)
fulc, ffulc = nfc, fnfc (fulc, ffulc) → (x0, y0) 对应位置a1
nfc, fnfc = xf, fx (nfc, fnfc) → (x0, y0) 对应位置a1
xf, fx= x, fu (fulc, ffulc) → (x1, y1) 对应位置为a1b1之间
-
第二次循环：
- 生成新的(x, fu) → (x2, y2)
- 更新：若满足条件 1-2:
fu <= fx & x > xf 函数上升
a2 = a1 = x0, b2 = xf = x1 (a1, b1) → (x0, x1)
fulc, ffulc = nfc, fnfc (fulc, ffulc) → (x0, y0) 对应位置a2
nfc, fnfc = xf, fx (nfc, fnfc) → (x1, y1) 对应位置b2
xf, fx= x, fu (fulc, ffulc) → (x2, y2) 对应位置为a2b2之间
-
第三次循环：
- 生成新的(x, fu) → (x3, y3)
- 更新：若满足条件 2-1-1:
fu > fx & x < xf 函数下降
a3 = x = x3, b3 = b2 = x1 (a3, b3) → (x3, x1)
fu <= fnfc (y3 <= y1) or nfc == xf (x1 == x2)
fulc, ffulc = nfc, fnfc (fulc, ffulc) → (x1, y1) 对应位置b3
nfc, fnfc = x, fu (nfc, fnfc) → (x3, y3) 对应位置a3
xf, fx (fulc, ffulc) → (x2, y2) 对应位置为a3b3之间
-
第四次循环：
- 生成新的(x, fu) → (x4, y4)
- 更新：若满足条件 2-2-2:
fu > fx & x 》= xf 函数上升
a4 = a3 = x3, b4 = x = x4 (a3, b3) → (x3, x4)
fu <= ffulc (y4 <= y1) or fulc == xf (x1 == x2) or fulc == nfc (x1 == x3)
fulc, ffulc = x, fu (fulc, ffulc) → (x4, y4) 对应位置a4
nfc, fnfc (nfc, fnfc) → (x3, y3) 对应位置b4
xf, fx (fulc, ffulc) → (x2, y2) 对应位置为a4b4之间
-
小结：
由以上过程可知：(fulc, ffulc)， (nfc, fnfc) 分别保存两个端点(a, b) 的函数值；(xf, fx) 保存两者之间的一个函数值，也可以说是目前最佳的迭代结果。而 fmin_data 却不如它名字那般是储存最小值，而是最新一次迭代的结果，在条件 2-x-x 中，它并不是最佳的迭代结果。fmin_data 在整个函数中唯一的作用是打印当前迭代结果，在翻译时可以忽略。
抛物线内插法：r, q, p
if np.abs(e) > tol1:
golden = 0
r = (xf - nfc) * (fx - ffulc)
q = (xf - fulc) * (fx - fnfc)
p = (xf - fulc) * q - (xf - nfc) * r
q = 2.0 * (q - r)
if q > 0.0:
p = -p
q = np.abs(q)
r = e
e = rat
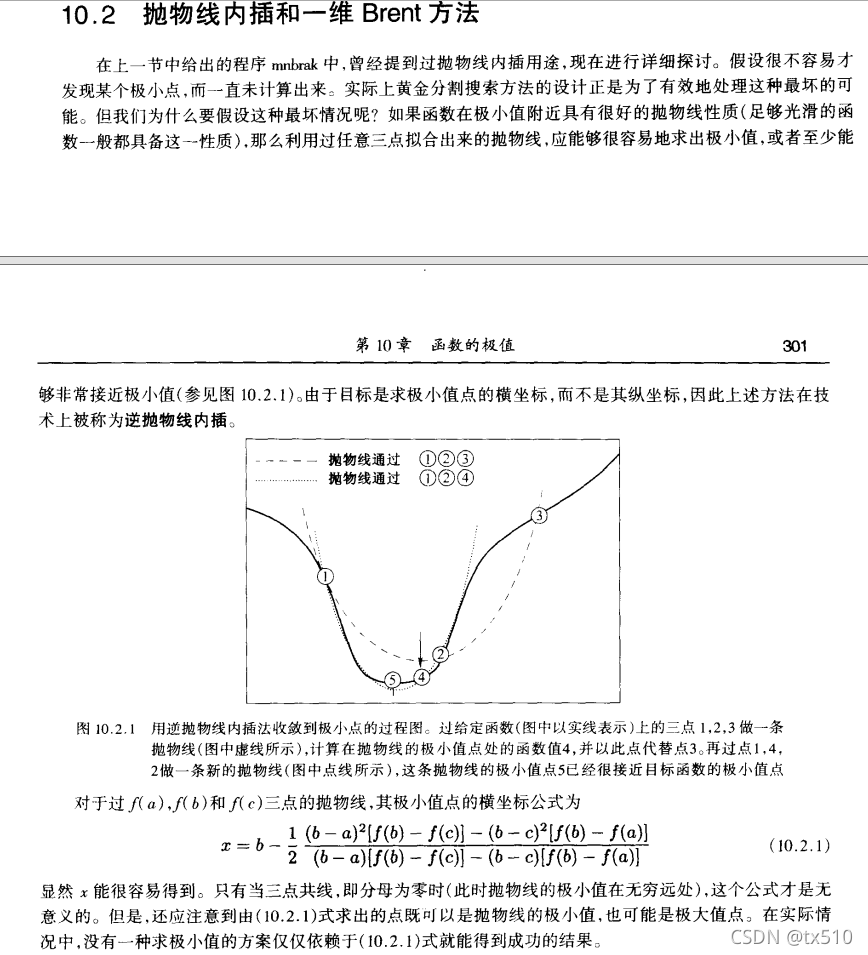
已知逆抛物线内插法公式：
对于过
f
(
a
)
f(a)
f(a)，
f
(
b
)
f(b)
f(b) 和
f
(
c
)
f(c)
f(c) 三点的抛物线，其极小值点的横坐标公式为
x
=
b
−
1
2
(
b
−
a
)
2
[
f
(
b
)
−
f
(
c
)
]
−
(
b
−
c
)
2
[
f
(
b
)
−
f
(
a
)
]
(
b
−
a
)
[
f
(
b
)
−
f
(
c
)
]
−
(
b
−
c
)
[
f
(
b
)
−
f
(
a
)
]
x = b - \frac{1}{2}\frac{(b - a)^2 [f(b) - f(c)] - (b - c)^2 [f(b) - f(a)]}{(b - a) [f(b) - f(c)] - (b - c)[f(b) - f(a)]}
x=b−21(b−a)[f(b)−f(c)]−(b−c)[f(b)−f(a)](b−a)2[f(b)−f(c)]−(b−c)2[f(b)−f(a)]
，其中
a
<
b
<
c
a < b < c
a<b<c 且
f
(
b
)
<
f
(
a
)
f(b) < f(a)
f(b)<f(a)，
f
(
b
)
<
f
(
c
)
f(b) < f(c)
f(b)<f(c)。
利用这个公式来理解r, q, p。
设 (fulc, ffulc) = (a, f(a))
(xf, fx) = (b, f(b))
(nfc, fnfc) = (c, f(c ))
其中 a < b < c，f(b) < f(a)，f(b) < f(c )
r = (xf - nfc) * (fx - ffulc) # = (b - c) * [f(b) - f(a)]
q = (xf - fulc) * (fx - fnfc) # = (b - a) * [f(b) - f(c)]
p = (xf - fulc) * q - (xf - nfc) * r
# = (b - a) * q - (b - c) * r
# = (b - a) ** 2 * [f(b) - f(c)] - (b - c) ** 2 * [f(b) - f(a)]
# 即内插公式的分子
q = 2.0 * (q - r) # 即内插公式的分母
if q > 0.0:
p = -p
q = np.abs(q)
# 这三行等同于：
# if q > 0.0: p = -p, q = q
# else: p = p, q = -q
# 这样保证 p / q 的结果前面为负号，而q非负
-
小结
这一部分是构造一个试探用的抛物线拟合。整个算法的思路就是：当函数不配合抛物线拟合的时候，用另一种收敛速度缓慢但很可靠的技巧（比如黄金分割搜索方法，即Brent算法）来求解，而在目标函数允许的情况下，转而使用逆抛物线内插法求解。
据此，下一个步骤为：判断抛物线内插是否合适。若合适，采用抛物线内插法；若不合适，在较长区间段采用黄金分割法。
判断是否使用抛物线内插法
# Check for acceptability of parabola
if ((np.abs(p) < np.abs(0.5*q*r)) and (p > q*(a - xf)) and
(p < q * (b - xf))):
rat = (p + 0.0) / q
x = xf + rat
step = ' parabolic'
if ((x - a) < tol2) or ((b - x) < tol2):
si = np.sign(xm - xf) + ((xm - xf) == 0)
rat = tol1 * si
else: # do a golden-section step
golden = 1
已知q非负。分析if内条件：（设逆抛物线内插法所得横坐标为 x0 ）
-
∣
p
∣
<
∣
0.5
×
q
×
r
∣
|p| < |0.5 × q × r|
∣p∣<∣0.5×q×r∣ 相当于
∣
p
∣
2
q
<
∣
r
∣
\frac{|p|}{2q} < |r|
2q∣p∣<∣r∣，即
x 0 = x f − p 2 q ∈ [ x f − ∣ r ∣ , x f + ∣ r ∣ ] x_0 = xf - \frac{p}{2q} \in [xf - |r|, xf + |r|] x0=xf−2qp∈[xf−∣r∣,xf+∣r∣] -
p
>
q
×
(
a
−
x
f
)
∪
p
<
q
×
(
b
−
x
f
)
p > q × (a - xf) \cup p < q× (b - xf)
p>q×(a−xf)∪p<q×(b−xf) 相当于
a − x f < p q < b − x f a - xf < \frac{p}{q} < b - xf a−xf<qp<b−xf
即
x f − b − x f 2 < x 0 < x f + x f − a 2 xf - \frac{b - xf}{2} < x_0 < xf + \frac{xf - a}{2} xf−2b−xf<x0<xf+2xf−a
根据参考书所说：
为了达到求解目的，抛物线必须满足：(i) 在限定区域(a, b)内下降；(ii) 从当前最佳值x移动的步长能够小于前面第二步移动步长的一半。后一条准则保证了内插步骤可以有效地收敛到某点，而不会在某一非收敛的有限范围内跳跃。
判定结果即满足条件 (ii) 。如果判定为真，则进行逆抛物线内插法，否则进行黄金分割法。
python.scipy._minimize_scalar_bounded 源代码
def _minimize_scalar_bounded(func, bounds, args=(),
xatol=1e-5, maxiter=500, disp=0,
**unknown_options):
"""
Options
-------
maxiter : int
Maximum number of iterations to perform.
disp: int, optional
If non-zero, print messages.
0 : no message printing.
1 : non-convergence notification messages only.
2 : print a message on convergence too.
3 : print iteration results.
xatol : float
Absolute error in solution `xopt` acceptable for convergence.
"""
_check_unknown_options(unknown_options)
maxfun = maxiter
# Test bounds are of correct form
if len(bounds) != 2:
raise ValueError('bounds must have two elements.')
x1, x2 = bounds
if not (is_array_scalar(x1) and is_array_scalar(x2)):
raise ValueError("Optimization bounds must be scalars"
" or array scalars.")
if x1 > x2:
raise ValueError("The lower bound exceeds the upper bound.")
flag = 0
header = ' Func-count x f(x) Procedure'
step = ' initial'
sqrt_eps = sqrt(2.2e-16)
golden_mean = 0.5 * (3.0 - sqrt(5.0))
a, b = x1, x2
fulc = a + golden_mean * (b - a)
nfc, xf = fulc, fulc
rat = e = 0.0
x = xf
fx = func(x, *args)
num = 1
fmin_data = (1, xf, fx)
fu = np.inf
ffulc = fnfc = fx
xm = 0.5 * (a + b)
tol1 = sqrt_eps * np.abs(xf) + xatol / 3.0
tol2 = 2.0 * tol1
if disp > 2:
print(" ")
print(header)
print("%5.0f %12.6g %12.6g %s" % (fmin_data + (step,)))
while (np.abs(xf - xm) > (tol2 - 0.5 * (b - a))):
golden = 1
# Check for parabolic fit
if np.abs(e) > tol1:
golden = 0
r = (xf - nfc) * (fx - ffulc)
q = (xf - fulc) * (fx - fnfc)
p = (xf - fulc) * q - (xf - nfc) * r
q = 2.0 * (q - r)
if q > 0.0:
p = -p
q = np.abs(q)
r = e
e = rat
# Check for acceptability of parabola
if ((np.abs(p) < np.abs(0.5*q*r)) and (p > q*(a - xf)) and
(p < q * (b - xf))):
rat = (p + 0.0) / q
x = xf + rat
step = ' parabolic'
if ((x - a) < tol2) or ((b - x) < tol2):
si = np.sign(xm - xf) + ((xm - xf) == 0)
rat = tol1 * si
else: # do a golden-section step
golden = 1
if golden: # do a golden-section step
if xf >= xm:
e = a - xf
else:
e = b - xf
rat = golden_mean*e
step = ' golden'
si = np.sign(rat) + (rat == 0)
x = xf + si * np.maximum(np.abs(rat), tol1)
fu = func(x, *args)
num += 1
fmin_data = (num, x, fu)
if disp > 2:
print("%5.0f %12.6g %12.6g %s" % (fmin_data + (step,)))
if fu <= fx:
if x >= xf:
a = xf
else:
b = xf
fulc, ffulc = nfc, fnfc
nfc, fnfc = xf, fx
xf, fx = x, fu
else:
if x < xf:
a = x
else:
b = x
if (fu <= fnfc) or (nfc == xf):
fulc, ffulc = nfc, fnfc
nfc, fnfc = x, fu
elif (fu <= ffulc) or (fulc == xf) or (fulc == nfc):
fulc, ffulc = x, fu
xm = 0.5 * (a + b)
tol1 = sqrt_eps * np.abs(xf) + xatol / 3.0
tol2 = 2.0 * tol1
if num >= maxfun:
flag = 1
break
if np.isnan(xf) or np.isnan(fx) or np.isnan(fu):
flag = 2
fval = fx
if disp > 0:
_endprint(x, flag, fval, maxfun, xatol, disp)
result = OptimizeResult(fun=fval, status=flag, success=(flag == 0),
message={0: 'Solution found.',
1: 'Maximum number of function calls '
'reached.',
2: _status_message['nan']}.get(flag, ''),
x=xf, nfev=num)
return result
翻译的c函数：(其中传递的函数指针只有一个double形参，如果函数还有其他形参，需要加上)
double sign(double x)
{
return (x >= 0.) ? 1. : -1.;
}
double MinimizerBrent(double (*func)(double), double x1, double x2)
{
double xatol, maxiter, sqrt_eps, golden_mean;
xatol = 1e-5;
maxiter = 500;
sqrt_eps = sqrt(2.2e-16);
golden_mean = 0.5 * (3. - sqrt(5.));
int flag = 0;
double a, b;
a = x1;
b = x2;
// x
double x, xf, fx, fulc, nfc;
fulc = a + golden_mean * (b - a);
x = xf = nfc = fulc;
fx = func(x);
double rat, e;
rat = e = 0.;
int num = 1;
// y
double fu, ffulc, fnfc;
ffulc = fnfc = fx;
double xm = 0.5 * (a + b);
double tol1, tol2;
tol1 = sqrt_eps * fabs(xf) + xatol / 3.;
tol2 = 2. * tol1;
int golden;
double r, q, p, si;
while (fabs(xf - xm) > (tol2 - 0.5 * (b - a)))
{
golden = 1;
if (fabs(e) > tol1)
{
golden = 0;
r = (xf - nfc) * (fx - ffulc);
q = (xf - fulc) * (fx - fnfc);
p = (xf - fulc) * q - (xf - nfc) * r;
q = 2. * (q - r);
if (q > 0.)
p = -p;
q = fabs(q);
r = e;
e = rat;
// Check for acceptability of parabola
if ((fabs(p) < fabs(0.5 * q * r)) && (p > q * (a - xf)) &&
(p < q * (b - xf)))
{
rat = (p + 0.) / q;
x = xf + rat;
if (((x - a) < tol2) || ((b - x) < tol2))
{
si = sign(xm - xf);
rat = tol1 * si;
}
}
else
golden = 1;
}
if (golden != 0)
{
if (xf > xm)
e = a - xf;
else
e = b - xf;
rat = golden_mean * e;
}
si = sign(rat);
x = xf + si * MAX(fabs(rat), tol1);
fu = func(x);
num++;
if (fu <= fx)
{
if (x > xf)
a = xf;
else
b = xf;
fulc = nfc;
ffulc = fnfc;
nfc = xf;
fnfc = fx;
xf = x;
fx = fu;
}
else
{
if (x < xf)
a = x;
else
b = x;
if ((fu <= fnfc) || (nfc == xf))
{
fulc = nfc;
ffulc = fnfc;
nfc = x;
fnfc = fu;
}
else if ((fu <= ffulc) || (fulc == xf) || (fulc == nfc))
{
fulc = x;
ffulc = fu;
}
}
xm = 0.5 * (a + b);
tol1 = sqrt_eps * fabs(xf) + xatol / 3.;
tol2 = 2. * tol1;
if (num >= maxiter)
{
flag = 1;
break;
}
}
// optimize result
if (flag == 0) printf("Success\n");
if (flag == 1) printf("Maxmimum number of function calls reached\n");
return xf;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
