LLMs-from-scratch ：embeddings 与 linear-layers 的对比

代码链接：https://github.com/rasbt/LLMs-from-scratch/blob/main/ch02/03_bonus_embedding-vs-matmul/embeddings-and-linear-layers.ipynb

《从零开始构建大型语言模型》一书的补充代码，作者：Sebastian Raschka 代码仓库：https://github.com/rasbt/LLMs-from-scratch

理解嵌入层和线性层之间的区别

• PyTorch 中的嵌入层与执行矩阵乘法的线性层实现相同的功能；我们使用嵌入层的原因是计算效率
• 我们将使用 PyTorch 中的代码示例逐步了解这种关系

import torch

print("PyTorch version:", torch.__version__)

PyTorch version: 2.5.1+cu124

 

使用 nn.Embedding

# 假设我们有以下 3 个训练示例，
# 它们可能代表 LLM 上下文中的标记 ID
idx = torch.tensor([2, 3, 1])

# 嵌入矩阵中的行数可以通过
# 获取最大标记 ID + 1 来确定。
# 如果最高标记 ID 是 3，那么我们需要 4 行，用于可能的
# 标记 ID 0, 1, 2, 3
num_idx = max(idx)+1

# 所需的嵌入维度是一个超参数
out_dim = 5

idx 

tensor([2, 3, 1])

num_idx

tensor(4)

• 让我们实现一个简单的嵌入层：

# 我们使用随机种子来保证可重现性，因为
# 嵌入层中的权重是用小的随机值初始化的
torch.manual_seed(123)

embedding = torch.nn.Embedding(num_idx, out_dim)

我们可以选择性地查看嵌入权重：

embedding.weight

Parameter containing:
tensor([[ 0.3374, -0.1778, -0.3035, -0.5880,  1.5810],
        [ 1.3010,  1.2753, -0.2010, -0.1606, -0.4015],
        [ 0.6957, -1.8061, -1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096, -0.4076,  0.7953]], requires_grad=True)

• 然后我们可以使用嵌入层来获取 ID 为 1 的训练示例的向量表示：

embedding(torch.tensor([1]))

tensor([[ 1.3010,  1.2753, -0.2010, -0.1606, -0.4015]],
       grad_fn=<EmbeddingBackward0>)

• 下面是底层发生的事情的可视化：

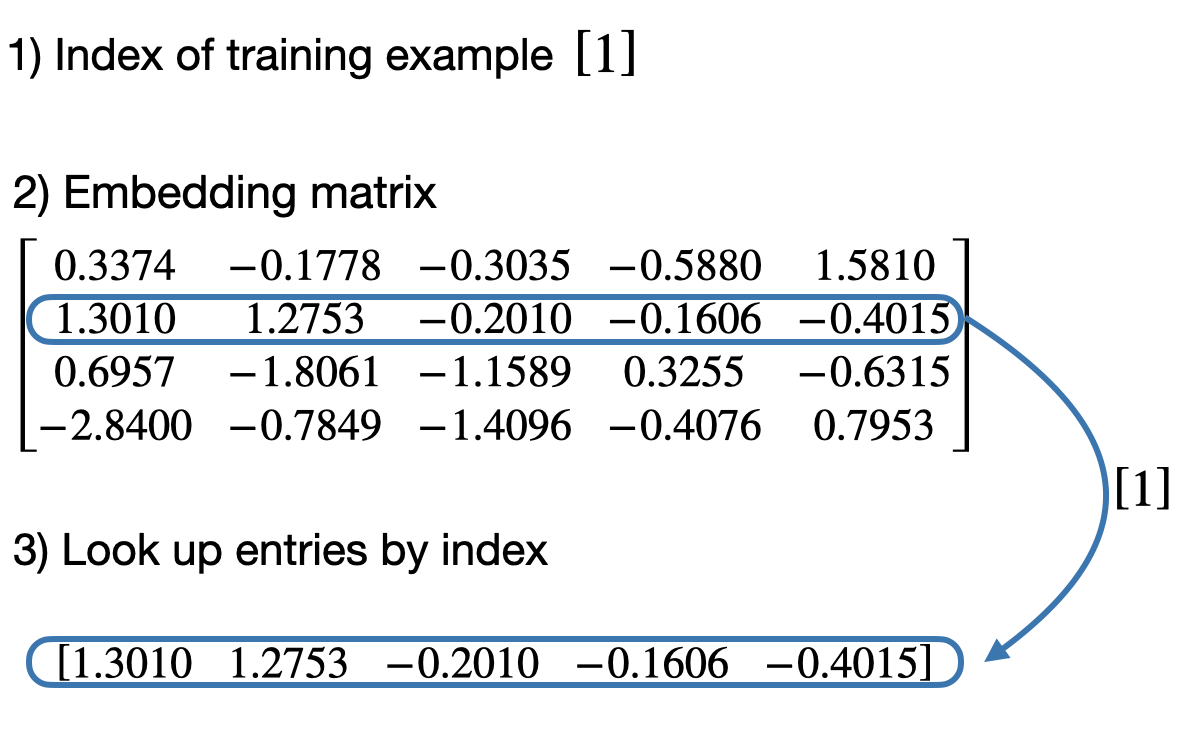
• 类似地，我们可以使用嵌入层来获取 ID 为 2 的训练示例的向量表示：

embedding(torch.tensor([2]))

tensor([[ 0.6957, -1.8061, -1.1589,  0.3255, -0.6315]],
       grad_fn=<EmbeddingBackward0>)

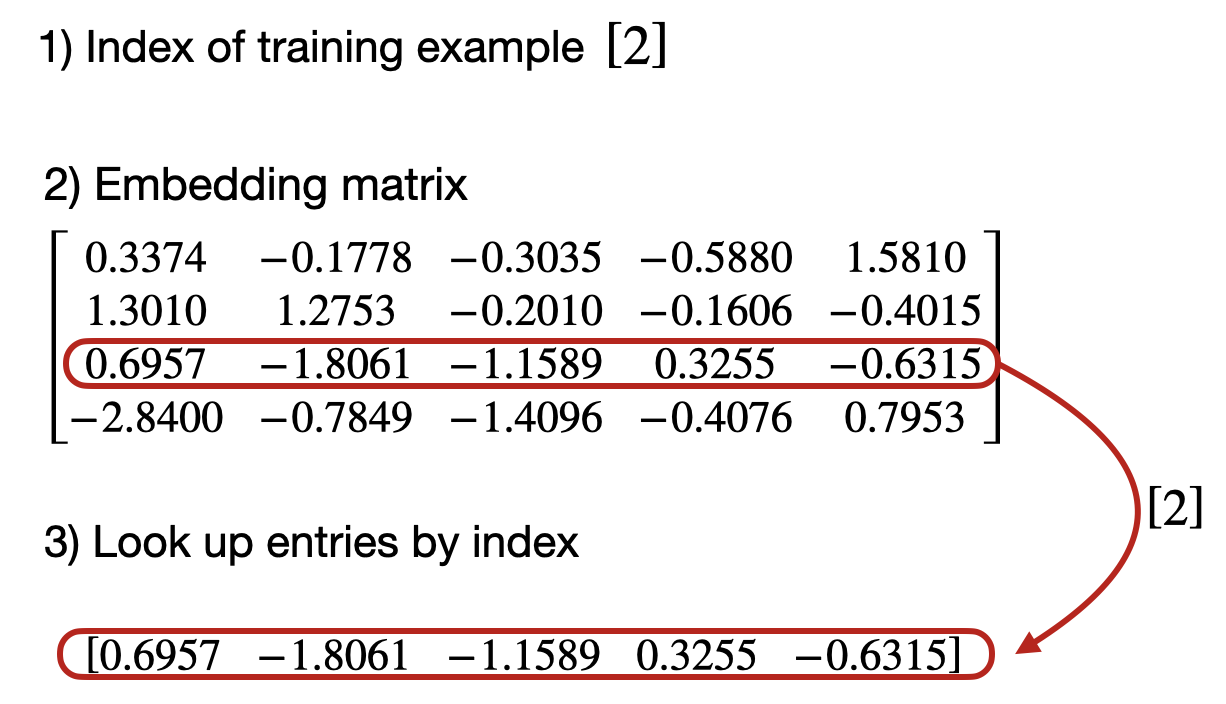
• 现在，让我们转换之前定义的所有训练示例：

idx = torch.tensor([2, 3, 1])
embedding(idx)

tensor([[ 0.6957, -1.8061, -1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096, -0.4076,  0.7953],
        [ 1.3010,  1.2753, -0.2010, -0.1606, -0.4015]],
       grad_fn=<EmbeddingBackward0>)

• 在底层，它仍然是相同的查找概念：

 

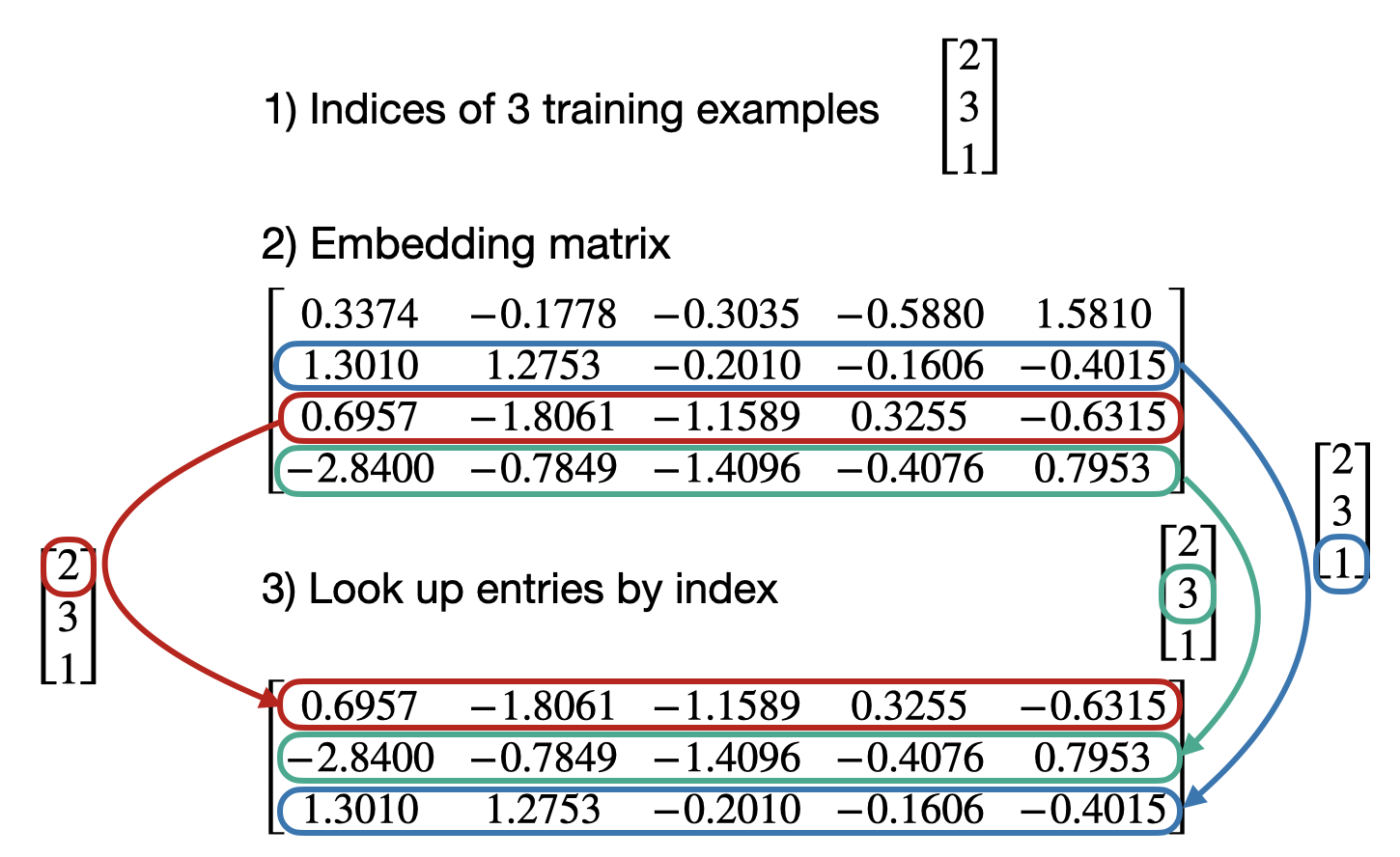
使用 nn.Linear

• 现在，我们将演示上面的嵌入层与在 PyTorch 中对独热编码表示使用 nn.Linear 层完全相同
• 首先，让我们将标记 ID 转换为独热表示：

onehot = torch.nn.functional.one_hot(idx)
onehot

tensor([[0, 0, 1, 0],
        [0, 0, 0, 1],
        [0, 1, 0, 0]])

• 接下来，我们初始化一个 Linear 层，它执行矩阵乘法 $X{W}^{\top }$：

torch.manual_seed(123)
linear = torch.nn.Linear(num_idx, out_dim, bias=False)
linear.weight

Parameter containing:
tensor([[-0.2039,  0.0166, -0.2483,  0.1886],
        [-0.4260,  0.3665, -0.3634, -0.3975],
        [-0.3159,  0.2264, -0.1847,  0.1871],
        [-0.4244, -0.3034, -0.1836, -0.0983],
        [-0.3814,  0.3274, -0.1179,  0.1605]], requires_grad=True)

• 请注意，PyTorch 中的线性层也是用小的随机权重初始化的；为了直接与上面的 Embedding 层进行比较，我们必须使用相同的小随机权重，这就是我们在这里重新分配它们的原因：

linear.weight = torch.nn.Parameter(embedding.weight.T)

linear.weight

Parameter containing:
tensor([[ 0.3374,  1.3010,  0.6957, -2.8400],
        [-0.1778,  1.2753, -1.8061, -0.7849],
        [-0.3035, -0.2010, -1.1589, -1.4096],
        [-0.5880, -0.1606,  0.3255, -0.4076],
        [ 1.5810, -0.4015, -0.6315,  0.7953]], requires_grad=True)

• 现在我们可以在输入的独热编码表示上使用线性层：

linear(onehot.float())

tensor([[ 0.6957, -1.8061, -1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096, -0.4076,  0.7953],
        [ 1.3010,  1.2753, -0.2010, -0.1606, -0.4015]], grad_fn=<MmBackward0>)

正如我们所看到的，这与我们使用嵌入层时得到的结果完全相同：

embedding(idx)

tensor([[ 0.6957, -1.8061, -1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096, -0.4076,  0.7953],
        [ 1.3010,  1.2753, -0.2010, -0.1606, -0.4015]],
       grad_fn=<EmbeddingBackward0>)

• 对于第一个训练示例的标记 ID，底层发生的计算如下：

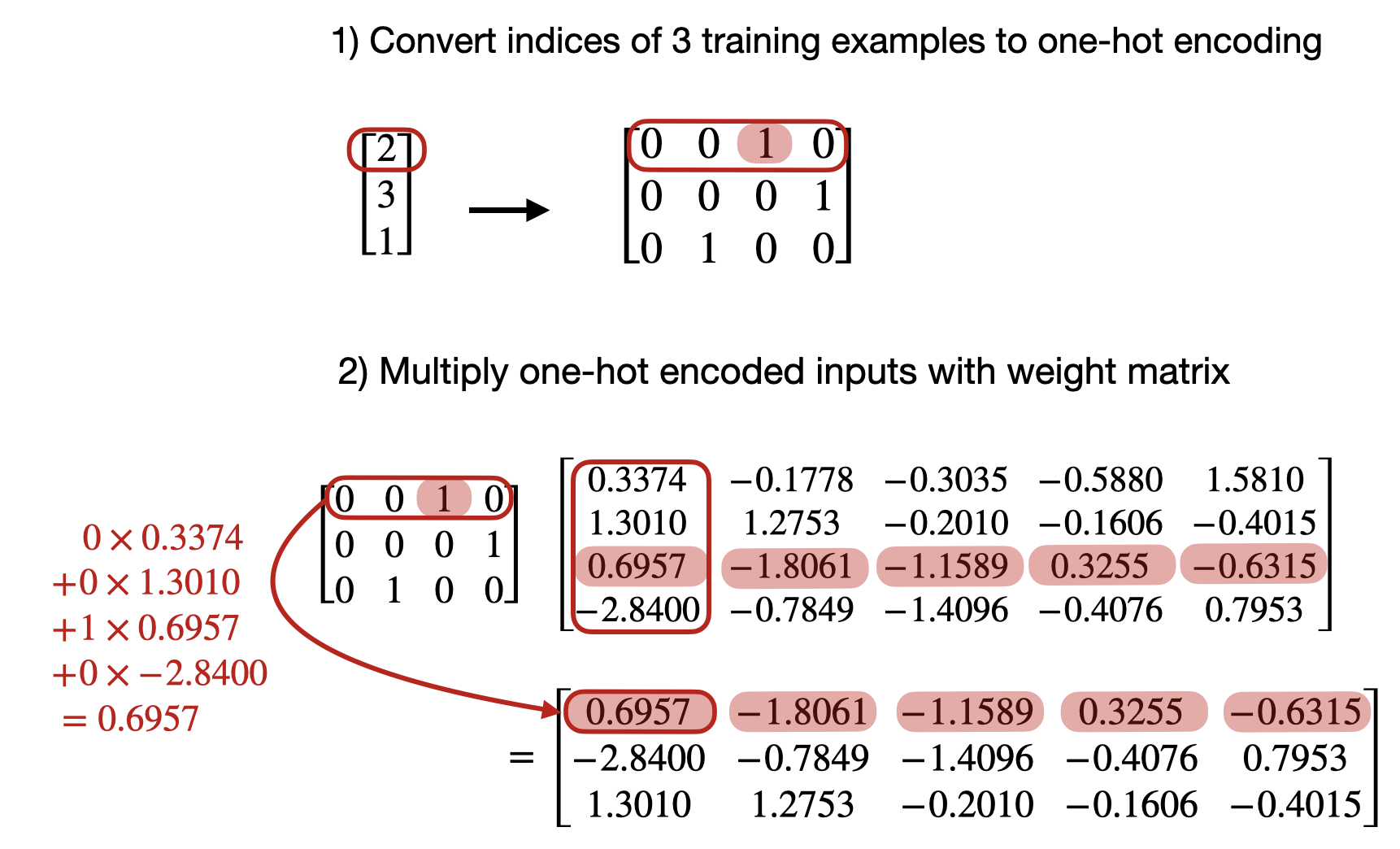
• 对于第二个训练示例的标记 ID：

• 由于每个独热编码行中除了一个索引外的所有索引都是 0（按设计），这种矩阵乘法本质上与独热元素的查找相同
• 这种在独热编码上使用矩阵乘法等价于嵌入层查找，但如果我们处理大型嵌入矩阵，可能会效率低下，因为有很多浪费的零乘法运算