动态规划

一、动态规划概论：

1、动态规划的基本要素：

（1）最优子结构性质：在一块块的子问题中，需要最优的解

（2）重叠子问题性质：子问题可能需要重复计算

2、动态规划算法的步骤：

·(1)找出最优解的性质，并刻划其结构特征。

·(2)递归地定义最优值。

·(3)以自底向上的方式计算出最优值。

·(4)根据计算最优值时得到的信息，构造最优解。

3、算法的思想：

（1）将整个问题划分成若干个子问题，整个问题的解依赖于子问题的解。

（2）子问题可能需要重复计算，因此可以使用一张表格来记录已经算出来的解

二、矩阵连乘问题

1、问题描述：有n个已经排好序的矩阵，确保是可以连乘的，求一个最优划分的方式来相乘，可以让所需要的相乘次数最少

2、理论基础：（1）两个AmsBsn相乘，所需要的乘法次数是msn

(2)一大堆矩阵相乘Ams……Bsn，相乘得到的矩阵的长和宽是Cmn

3、解题的思路：

（1）搞清楚最优解的性质和结构关系：

一段长度的矩阵连乘得到的最优解是：将该段矩阵从某处（这一处需要循环的计算来选择出来min的那个）断成两截相乘，其中每一节的相乘次数也是最优的。

（2）写出递归关系：

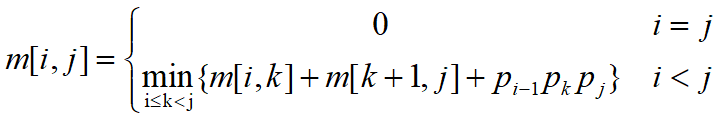
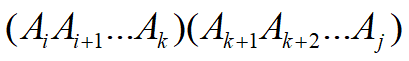
其中数组p的下标代表的是第i个数组的宽

（3）计算最优值：

列两个表格，一个s,一个m:

s:断开位置；m:最优的相乘次数

（4）计算最优解：查表。先查找最终的，再递归进行查找分开的两部分如何构造的。

4、时间复杂度：O(n^3)

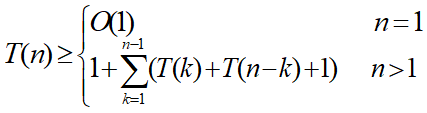
5、

•递归算法求解时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称