机器学习——线性回归算法

模型表示

为了建立将来使用的符号，我们将使用x^ (i)表示“输入”变量(本例中的区域)，也称为输入特征，以及y^(i)表示我们试图预测的“产量”或目标变量。一对(x,y)称为训练示例，我们将使用的数据集—m个训练示例的列表(x(i)，y(i));i=1，…，m称为训练集。注意，符号中的上标“(i)”只是训练集的索引，与取幂无关。我们还将使用X表示输入值的空间，Y表示输出值的空间。

假设函数

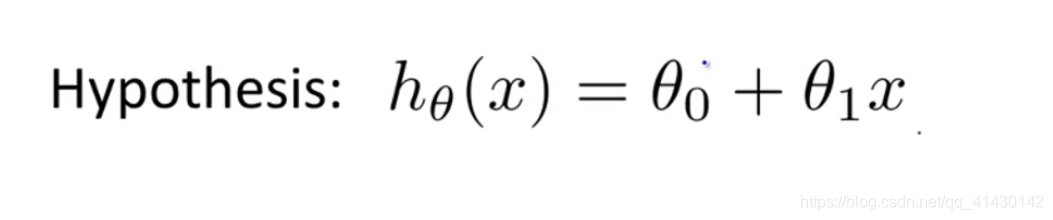
代价函数

我们可以用代价函数来衡量假设函数的准确性。它取假设的所有结果的平均值差(实际上是平均值的更准确的版本)，其中输入x，实际输出y。

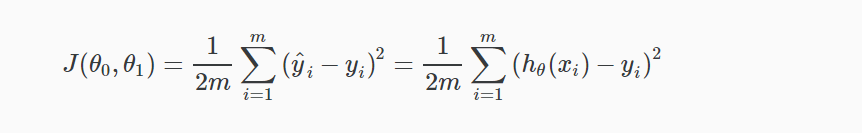
我们最终的目的是找到合适的(θ0,θ1)使代价取到最小。

1. 简化的单变量只有θ1时，假设函数的图像是一条过原点的直线。而代价函数则是一条二次函数的图像曲线，y轴代表的是代价函数J(θ)的值，X轴代表的是θ1的值，我们只需要找到图像最低点对应的θ1值即可。
2. 当取值为双变量时，即变量有θ0，θ1时。代价函数图像如下：
   

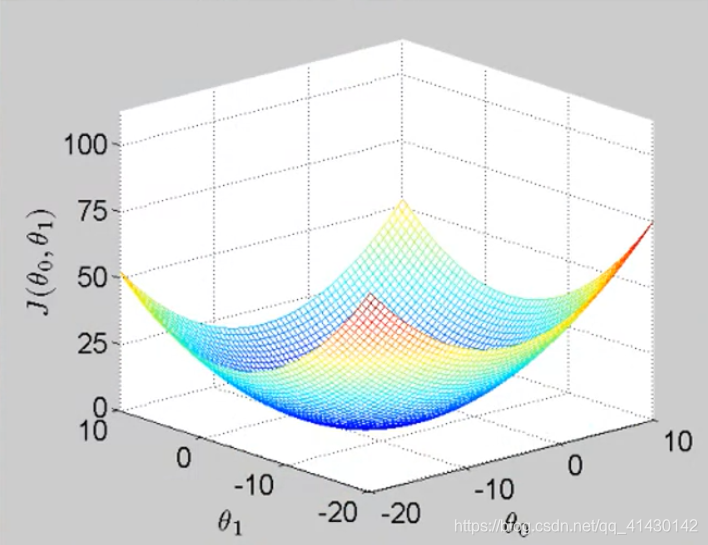
为了简化这种三维图像，我们引入等高线图这个图像概念。
等高线图是包含许多等高线的图形。双变量函数的等高线在同一行的所有点处具有恒定值。这种图表的一个例子如下：

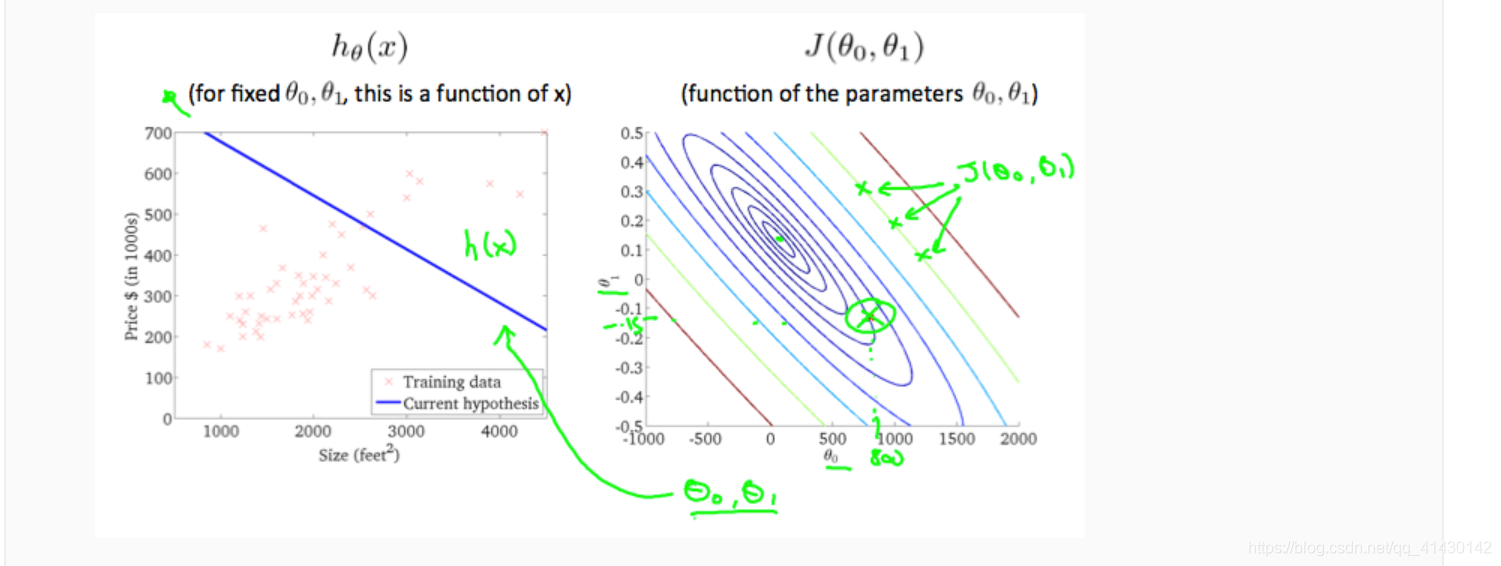
采用任何颜色并沿着’圆’，人们可以期望得到相同的成本函数值。例如，上面绿线上的三个绿点具有相同的值J(θ0,θ1)作为结果，它们沿同一条线中。带圆圈的x显示左侧图形的成本函数的值θ0=800和θ1=–0.15。从图中我们可以看到得到的假设函数图像和我们的数据拟合的很不好。

取另一个h（x）并绘制其等高线图，可得到以下图表：

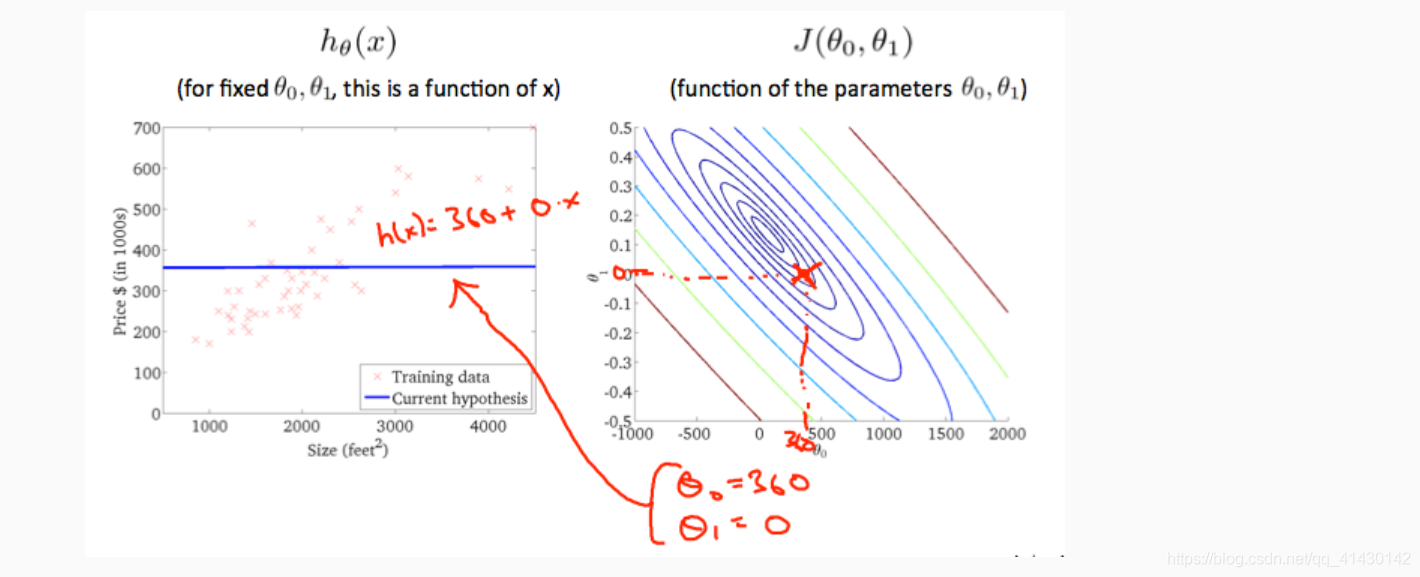
这时θ0=360和θ1=0，在等高线图中靠近中心，从而减少了代价函数的误差，现在得到的假设函数略微拟合我们的数据。

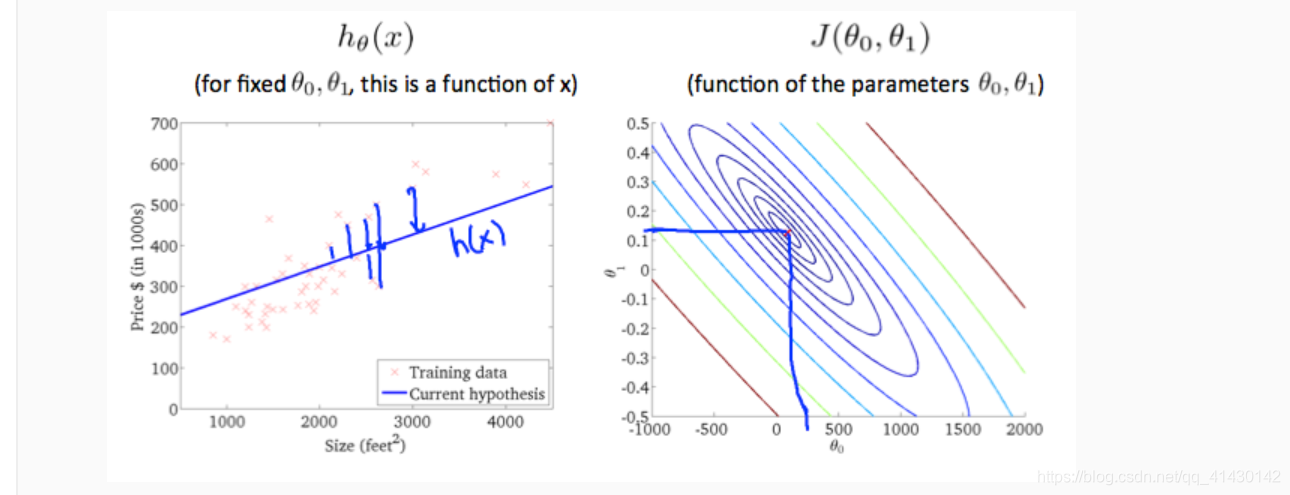
上图最大限度地降低了成本函数，从而最终使结果最小化 θ1，θ0约为0.12和250。在我们的图表右侧绘制这些值似乎将我们的观点置于最内圈“圆圈”的中心。

梯度下降算法

我们已经定义了代价函数J。下面介绍梯度下降这种算法，种算法可以将代价函数J最小化，梯度下降是很常用的算法，它不仅被用在线性回归上，它实际上被广泛的应用于机器学习领域中的众多领域。
梯度下降算法讲解