本文探讨了在不同定期存款利率下，如何通过算法计算出最优的存款策略，以实现20年后收益最大化。通过分析不同存款期限的复利效应，文章提供了具体的C语言代码实现，展示了如何遍历所有可能的存款组合，找出最佳方案。
银行定期存款有3月期，半年期，一年期，2年期，3年期，5年期等多种，不同存期的年利水平是不同的。
0.36 期限=活期 1.71 期限=3个月 1.98 期限=6个月 2.25 期限=1年
2.79 期限=2年 3.33 期限=3年 3.60 期限=5年
假设在银行存1万元，计划存款期限为20年，这是可以有多种方案，例如
按5年期存，每满5年又将本利再存5年，这样，可以存4次
按3年期存，每满3年又将本利再存3年，这样，可以连续存6次，最后剩下2年再存2年期1次
按1年期存，每满5年又将本利再存续存，这样，可以存20次
利息=本金*月息利率*12*存款年限
现在某人手中又1万元钱，请通过计算选择一种存钱方案，使得存入银行20年后得到的利息最多(假定银行对超过存款期限的那一部分时间不付利息)。
分析：假设用1万本金连续存5年期4次，基本合计可用下面的公式计算
第一期：10000*(1+5*3.6/100)
第二期：10000*(1+5*3.6/100)²
第三期：10000*(1+5*3.6/100)³
第四期：10000*(1+5*3.6/100)⁴
#include<stdio.h>
#include<math.h>
int main()
{
double rate[7];
//保存6种整存整取的利率(活期，3个月，半年，一年，三年，五年)
double money,total,temp; //计划存入金额
int month,j; //计划存钱的总月数
int y5,y3,y2,y1,y01,y02,y03; //分别表示使用不同档存钱的次数
int timer[7];
//按题目的内容设置利率,也可以自己输入
rate[0]=0.36;
rate[1]=1.71;
rate[2]=1.98;
rate[3]=2.25;
rate[4]=2.79;
rate[5]=3.33;
rate[6]=3.60;
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 存钱利息最大化 *\n");
printf("\t* *\n");
printf("\t****************************\n");
printf("输入存款总数:");
scanf("%lf",&money);
printf("输入存款总月数:");
scanf("%d",&month);
for(j=0;j<=6;j++){
rate[j]=rate[j]/12/100;
}
total=money;
y5=0;
do{
y3=0;
do{
y2=0;
do{
y1=0;
do{
y01=0;
do{
y02=0;
do{
//剩余月数按活期算
y03=month-60*y5-36*y3-24*y2-12*y1-6*y01-3*y02;
if(y03<0)
break; //如果存款月份超过总月数，跳出循环
temp=money*pow(1+rate[1]*3,(double)y02)
*pow(1+rate[2]*6,(double)y01)
*pow(1+rate[3]*12,(double)y1)
*pow(1+rate[4]*12*2,(double)y2)
*pow(1+rate[5]*12*3,(double)y3)
*pow(1+rate[6]*12*5,(double)y5)
*pow(1+rate[0],(double)y03);
if(temp>total){
total=temp;
timer[0]=y03;
timer[1]=y02;
timer[2]=y01;
timer[3]=y1;
timer[4]=y2;
timer[5]=y3;
timer[6]=y5;
}
y02++; //增加一次3月期
}while(y02<=(month-60*y5-36*y3-24*y2-12*y1-6*y01)/3);
y01++; //增加一次半年期
}while(y01<=(month-60*y5-36*y3-24*y2-12*y1));
y1++; //增加一次1年期
}while(y1<=(month-60*y5-36*y3-24*y2)/12);
y2++; //增加一次2年期
}while(y2<=(month-60*y5-36*y3)/24);
y3++; //增加一次3年期
}while(y3<=(month-60*y5)/36);
y5++; //增加一次5年期
}while(y5<=month/60);
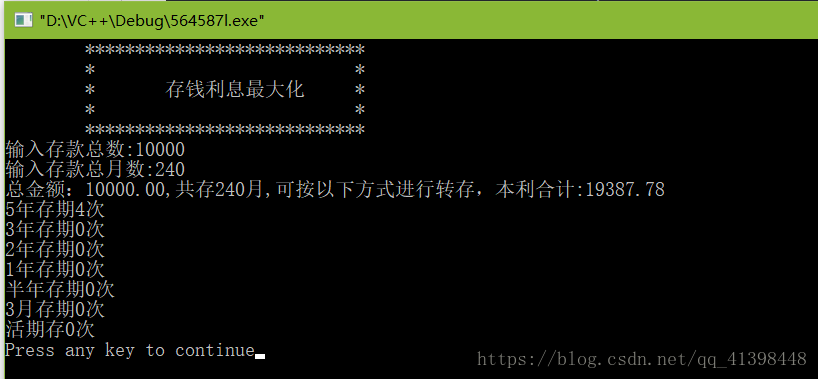
printf("总金额：%.2lf,共存%d月,可按以下方式进行转存，本利合计:%.2lf\n",money,month,total);
printf("5年存期%d次\n",timer[6]);
printf("3年存期%d次\n",timer[5]);
printf("2年存期%d次\n",timer[4]);
printf("1年存期%d次\n",timer[3]);
printf("半年存期%d次\n",timer[2]);
printf("3月存期%d次\n",timer[1]);
printf("活期存%d次\n",timer[0]);
return 0;
}
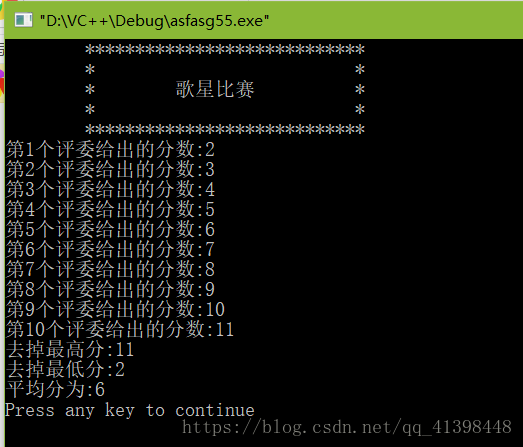
在歌星大赛种，有10个评委为参赛的选手打分，分数为1~100分。选手最后得分为：去掉一个最高分和一个最低分去其余8个分数的平均值。
#include<stdio.h>
void main()
{
int integer,i,max,min,sum;
max=-32768; //假设当前的最大值max为C语言整型数的最小值
min=32767; //假设当前的最大值min为C语言整型数的最大值
sum=0;
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 歌星比赛 *\n");
printf("\t* *\n");
printf("\t****************************\n");
for(i=1;i<=10;i++){
printf("第%d个评委给出的分数:",i);
scanf("%d",&integer);
sum+=integer;
if(integer>max)
max=integer;
if(integer<min)
min=integer;
}
printf("去掉最高分:%d\n",max);
printf("去掉最低分:%d\n",min);
printf("平均分为:%d\n",(sum-max-min)/8);
}
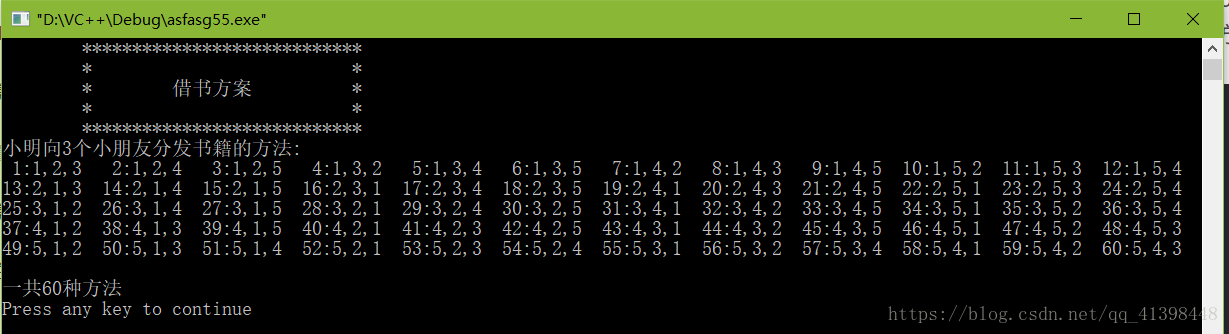
小明有5本新书，要借给A,B,C三位小朋友，若每人每次只能借一本，则可以有多少种不同的借法？
分析：本问题实际上是一个排列问题，即从5个中取3个进行排列的方法的总数。首先先对5本书从1到5进行编号，然后使用穷举法。假设3个人分别借这5本书中的一本，党3个人所借的书的编号不相同时，就是满足题意的一种借阅方法。
#include<stdio.h>
void main()
{
int a,b,c,count=0;
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 借书方案 *\n");
printf("\t* *\n");
printf("\t****************************\n");
printf("小明向3个小朋友分发书籍的方法:\n");
for(a=1;a<=5;a++){ //穷举第一个人借5本书中的一本的全部情况
for(b=1;b<=5;b++){ //穷举第二个人借5本书中的一本的全部情况
for(c=1;a!=b&&c<=5;c++){ //当前两个人借不同的书时，穷举第3个人借5本书中的一本的全部情况
if(c!=a&&c!=b){
printf(count%8?"%2d:%d,%d,%d ":"%2d:%d,%d,%d ",++count,a,b,c);
}
}
}
}
printf("\n一共%d种方法\n",count);
}
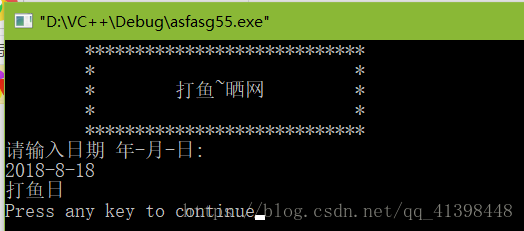
中国有句俗语“三天打鱼两天晒网”。某人从1990年1月1日开始“三天打鱼两天晒网”，问这个人在以后的某一天中是“打鱼”还是“晒网”？
分析：根据题意可以将解题步骤分为3步
(1)计算从1990年1月1日开始至指定日期共有多少天；
(2)由于"打鱼"和"晒网"的周期为5天，所以将计算出的天数用5天去除；
(3)根据余数判断他是在"打鱼",否则是在"晒网"
如果余数是1 2 3 则是在"打鱼"，否则是在"晒网"
#include<stdio.h>
#define YEAR 1990
#define DAYS 365
int a[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int TotalDays(int year,int month,int day)
{
int i=year-YEAR;
int i_month=1;
int totalday=day;
if(year%4==0&&year%100!=0){
a[2]=29;
}
while(i_month<month){
totalday+=a[i_month++];
}
if(i>0){
totalday+=DAYS*i+(i-1)/4+1;
}
return totalday;
}
void main()
{
int totalday;
int year,month,day;
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 打鱼~晒网 *\n");
printf("\t* *\n");
printf("\t****************************\n");
printf("请输入日期 年-月-日:\n");
scanf("%d-%d-%d",&year,&month,&day);
totalday=TotalDays(year,month,day);
if(totalday%5==0||totalday%5==4){
printf("晒网日\n");
}
else{
printf("打鱼日\n");
}
}
某天夜里，A,B,C,D,E五人一块去捕鱼，到第二天凌晨时都疲惫不堪，于是各自找地方睡觉。天亮了，A第一个醒来，他将鱼分成5份，把多余的一条鱼扔掉，拿走自己的一份。B第二个醒来，也将鱼分为5份，把多余的一条鱼扔掉，也拿走了自己的一份。C,D,E一次醒来，也按同样的方法拿走鱼。问他们合捕了多少条鱼？
分析:根据题意，总计将所有的鱼进行了5次平均分配，每次分配时的策略是相同的，即扔掉一条鱼正好分成5份，然后拿走自己的一份，余下其他的4份。
假定鱼的总数为X，则X可以按照题目的要求进行5次分配：X-1后可被5整除，余下的鱼为4*(X-1)/5。若X满足上述要求，则X就是题目的解
#include<stdio.h>
void main()
{
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 捕鱼和分鱼 *\n");
printf("\t* *\n");
printf("\t****************************\n");
int n,i,x,flag=1;
for(n=6;flag!=0;n++){ //采用试探的方法。令试探值n逐步加大
for(x=n,i=1&&flag;i<=5;i++)
if((x-1)%5==0)
x=4*(x-1)/5;
else
flag=0; //若步能分配则置标记flag=0退出分配
if(flag)
break; //若分配过程正常结束则找到结果则退出试探的过程
else
flag=1; //否则继续试探下一个数
}
printf("他们一共捕捉了%d条鱼\n",n);
}
鱼商A将养的一缸金鱼分5次出售，第一次卖出全部的一半加二分之一条；第二次卖出余下的三分之一加三分之一条；第三次卖出余下的四分之一加四分之一条；第4次卖出余下的五分之一加五分之一条；最后卖出余下的11条。问原来鱼缸共有多少条金鱼？
分析：题目中所有的鱼是分5次出售的，每次卖出的策略相同；第j次卖剩下的1/(j+1)再加1/(j+1)条。第5次将第4次余下的11条全卖完了
假定第j次鱼的总数为X，则第j次留下： x-(x+1)/(j+1)
当第4次出售完毕时，应该剩下11条。若X满足上述要求，则X就是题目的解
应该注意的是：(x+1)/(j+1)应该满足整除条件。试探X的初值可以从23开始，试探的步长为2，因为X的值一定为奇数
#include<stdio.h>
void main()
{
int i,j,flag=0,x;
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 鱼缸的鱼 *\n");
printf("\t* *\n");
printf("\t****************************\n");
for(i=23;flag==0;i+=2){ //控制试探的步长和过程
for(j=1,x=i;j<=4&&x>=11;j++) //完成4次出售的操作
if((x+1)%(j+1)==0){ //若满足整除条件则进行实际的出售操作
x-=(x+1)/(j+1);
}
else{ //否则停止计算过程
x=0;
break;
}
if(j==5&&x==11){ //若第4次余下11条则满足题意
printf("鱼缸原来有%d条鱼\n",i);
flag=1;
}
}
}
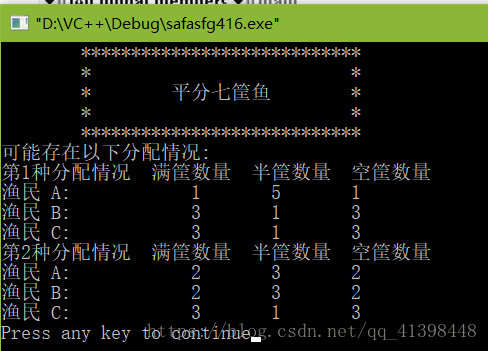
甲,乙,丙3位预付出海打鱼，他们随船带了21只箩筐。返航时发现有7筐装满了鱼，还有7筐装满了鱼，另外7筐是空的，由于他们没有称，只好通过目测认为7个满眶鱼的重量是相等的，7个半筐鱼的重量是相等的。在不将鱼倒出来的前提下，怎样和筐平为3筐份？
分析：根据题意可知：每个人应分得7个箩筐，其中有3.5筐鱼。使用一个3*3数组a来表示3个人分到得东西。其中每个人对应数组a得一行，数组得第0列放分到的鱼的整数筐，数组的第1列放分到的半筐数，数组的第2列放分到的空筐数。由题目可以退出：
数组的每行或每列的元素之和都为7
对数组的行来说，满筐数加半筐数=3.5
每个人所得的满筐数不能超过3筐
每个人都必须至少由1个半筐，且半筐数一定为奇数
#include<stdio.h>
int a[3][3],count=0;
void main()
{
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 平分七筐鱼 *\n");
printf("\t* *\n");
printf("\t****************************\n");
int i,j,k,m,n,flag;
printf("可能存在以下分配情况:\n");
for(i=0;i<=3;i++){ //试探第一个人满筐a[0][0]的值，满筐数不能>3
a[0][0]=i;
for(j=i;j<=7-i&&j<=3;j++){ //试探第二个人满筐a[1][0]的值,满筐数不能>3
a[1][0]=j;
if((a[2][0]=7-j-a[0][0])>3) //第3个人满筐数不能>3
continue;
if(a[2][0]<a[1][0]) //要求最后一个人分的筐数>=前一个人，排除重复情况
break;
for(k=1;k<=5;k+=2){ //试探半筐a[0][1]的值，半筐数为奇数
a[0][1]=k;
for(m=1;m<7-k;m+=2){
a[1][1]=m;
a[2][1]=7-k-m;
for(flag=1,n=0;flag&&n<3;n++)
//判断每个人分到的鱼是3.5筐,flag为满足的题意的标记变量
if(a[n][0]+a[n][1]<7&&a[n][0]*2+a[n][1]==7)
a[n][2]=7-a[n][0]-a[n][1]; //计算应得到的空筐量
else
flag=0; //不符合题意则置标记为0
if(flag){
printf("第%d种分配情况 满筐数量 半筐数量 空筐数量\n",++count);
for(n=0;n<3;n++){
printf("渔民 %c: \t%4d\t%4d\t%4d\n",'A'+n,a[n][0],a[n][1],a[n][2]);
}
}
}
}
}
}
}
背包问题
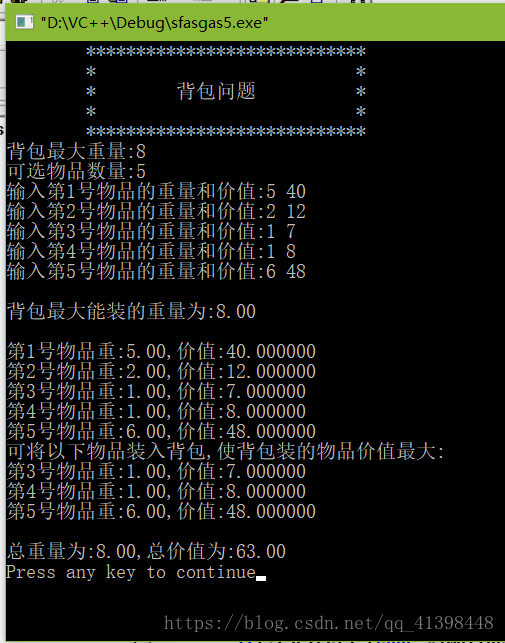
有一个背包最多能装8kg物品,假设要使背包能装下下面的水果，并要求背包里面的水果价值最大，问应该装哪些水果符合要求？
苹果：5kg,40元
梨:2kg,12元
桃:1kg,7元
葡萄:1lg,8元
香蕉:6kg,48元
#include<stdio.h>
#include<stdlib.h>
//定义结构goods，用于保存水果的的相关信息
typedef struct goods
{
double *weight; //重量
double *value; //价值
char *select; //是否选择方案
int num; //物品数量
double limitw; //限制重量
}GOODS;
//定义全局变量
double maxvalue,totalvalue; //方案最大价值，物品总价值
char *select1; //临时数组
//定义函数backpack(),通过递归方法完成背包的装入
void backpack(GOODS *g,int i,double tw,double tv)
//参数为物品i，当前选择已经达到得重量tw,本方案可能达到的总价值
{
int k;
if(tw+g->weight[i]<=g->limitw){
//参数为物品i包含在当前方案，且重量小于等于限制重量
select1[i]=1; //选中第i个物品
if(i<g->num-1){ //若物品i不是最后一个物品
backpack(g,i+1,tw+g->weight[i],tv); //递归调用，继续添加下一个物品
}
else{ //已经到最后一个物品
for(k=0;k<g->num;++k) //将状态标志复制到option数组中
g->select[k]=select1[k];
maxvalue=tv; //保存当前方案的最大价值
}
}
select1[i]=0; //取消物品i的选择状态
if(tv-g->value[i]>maxvalue){
//若物品总价减去物品i的价值还大于maxv方案已有的价值，说明还可以继续向方案中添加物品
if(i<g->num-1) //物品i不是最后一个物品
backpack(g,i+1,tw,tv-g->value[i]); //递归调用，继续添加下一个物品
else{ //若已经到最后一个物品
for(k=0;k<g->num;++k) //将状态标志复制到option数组中
g->select[k]=select1[k];
maxvalue=tv-g->value[i];//保存当前方案的最大价值(从物品总价值中减去物品i的价值)
}
}
}
void main()
{
printf("\t****************************\n");
printf("\t* *\n");
printf("\t* 背包问题 *\n");
printf("\t* *\n");
printf("\t****************************\n");
double sumweight;
GOODS g;
int i;
printf("背包最大重量:");
scanf("%lf",&g.limitw);
printf("可选物品数量:");
scanf("%d",&g.num);
if(!(g.value=(double *)malloc(sizeof(double)*g.num))){ //分配内存保存物品价值
printf("内存分配失败");
exit(0);
}
if(!(g.weight=(double *)malloc(sizeof(double)*g.num))){ //分配内存保存物品的重量
printf("内存分配失败\n");
exit(0);
}
if(!(g.select=(char *)malloc(sizeof(char)*g.num))){ //分配内存保存物品的重量
printf("内存分配失败\n");
exit(0);
}
if(!(select1=(char *)malloc(sizeof(char)*g.num))){ //分配内存保存物品的重量
printf("内存分配失败\n");
exit(0);
}
totalvalue=0;
for(i=0;i<g.num;i++){
printf("输入第%d号物品的重量和价值:",i+1);
scanf("%lf%lf",&g.weight[i],&g.value[i]);
totalvalue+=g.value[i]; //统计所有物品的价值总和
}
printf("\n背包最大能装的重量为:%.2f\n\n",g.limitw);
for(i=0;i<g.num;i++)
printf("第%d号物品重:%.2f,价值:%2f\n",i+1,g.weight[i],g.value[i]);
for(i=0;i<g.num;i++)
select1[i]=0; //初始设各物品都没有加入选择集
maxvalue=0; //加入方案物品的总价值
backpack(&g,0,0.0,totalvalue);
//第0号物品加入方案，总重量为0，所有物品价值为totalvalue
sumweight=0;
printf("可将以下物品装入背包,使背包装的物品价值最大:\n");
for(i=0;i<g.num;++i){
if(g.select[i]){
printf("第%d号物品重:%.2f,价值:%2f\n",i+1,g.weight[i],g.value[i]);
sumweight+=g.weight[i];
}
}
printf("\n总重量为:%.2f,总价值为:%.2f\n",sumweight,maxvalue);
}
扫一扫
2124
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
