分治算法

大数相乘

实现大数相乘，即计算两个大数的积

算法思想：例如123*456的分治算法如下。

第一次拆分为：12和45

设 char *a="123",*b="456",对a实现t=strlen(a),t/2得12（0，1位置）余3(2位置)为3和6。同理，对另一部分b来说也是相同的，即拆分为456.

使用递归求解：12*45，求得12*45的结果左移两位补0右边，因为实际上是120*450。

12*6（同上左移一位其实是120*6）.

3*45（3*450）。

3*6（3*6解的结果不移动）。

第二次：12和45，说明如下：

1和4：交叉相乘并将结果相加，1*4左移两位为400，1*5左移一位为50，2*4左移一位为80，2*5不移位为10.

2和5：相加得400+50+80+10=540.

另外几个不需要拆分得72，135，18，所以：54000+720+1350+18=56088。

由此可见，整个解法得难点是对分治的理解，以及结果的调整和对结果的合并。

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<string.h>

char *result='\0';
int pr=1;

void getFill(char *a,char *b,int ia,int ja,int ib,int jb,int tbool,int move)
{
     int r,m,n,s,j,t;
	 char *stack;
	 
	 m=a[ia]-48;
	 if(tbool){   //直接从结果数组得标志位填入，这里用了栈堆思想
	     r=(jb-ib>ja-ia)?(jb-ib):(ja-ia);
		 stack=(char*)malloc(r+4);
		 for(r=j=0,s=jb;s>=ib;r++,s--){
		       n=b[s]-48;
			   stack[r]=(m*n+j)%10;
			   j=(m*n+j)/10;
		 }
		 if(j){
		       stack[r]=j;
			   r++;
		 }
		 for(r--;r>=0;r--,pr++){
		       result[pr]=stack[r];
		 }
     free(stack);
	 for(move=move+pr;pr<move;pr++){
	     result[pr]='\0';
	     }
	    }
	 else{  //与结果得某几位相加，这里不改变标志位pr的值
	      r=pr-move-1;
		  for(s=jb,j=0;s>=ib;r--,s--){
		      n=b[s]-48;
			  t=m*n+j+result[r];
			  result[r]=t%10;
			  j=t/10;
		   }
		   for(;j;r--){
		      t=j+result[r];
			  result[r]=t%10;
			  j=t/10;
		   }
	}
}

int get(char *a,char *b,int ia,int ja,int ib,int jb,int t,int move){
    int m,n,s,j;
	if(ia==ja){
	    getFill(a,b,ia,ja,ib,jb,t,move);
		return 1;
	}
	else if(ib==jb){
	    getFill(b,a,ib,jb,ia,ja,t,move);
		return 1;
	}
	else{
	   m=(ja+ia)/2;
	   n=(jb+ib)/2;
	   s=ja-m;
	   j=jb-n;
	   get(a,b,ia,m,ib,n,t,s+j+move);
	   get(a,b,ia,m,n+1,jb,0,s+move);
	   get(a,b,m+1,ja,ib,n,0,j+move);
	   get(a,b,m+1,ja,n+1,jb,0,0+move);
	}
	return 0;
}

void main()
{
  char *a,*b;
  int n,flag;
  a=(char*)malloc(1000);
  b=(char*)malloc(1000);
  printf("The program will computer a*b\n");
  printf("Enter a b:");
  scanf("%s %s",a,b);
  result=(char*)malloc(strlen(a)+strlen(b)+2);
  flag=pr=1;
  result[0]='\0';
  if(a[0]=='-'&&b[0]=='-'){
       get(a,b,1,strlen(a)-1,1,strlen(b)-1,1,0);
  }
  if(a[0]=='-'&&b[0]!='-'){
       flag=0;
	   get(a,b,1,strlen(a)-1,0,strlen(b)-1,1,0);
  }
  if(a[0]!='-'&&b[0]=='-'){
       flag=0;
	   get(a,b,0,strlen(a)-1,1,strlen(b)-1,1,0);
  }
  if(a[0]!='-'&&b[0]!='-'){
       get(a,b,0,strlen(a)-1,0,strlen(b)-1,1,0);
  }
  if(!flag){
       printf("-");
  }
  if(result[0]){
       printf("%d",result[0]);
  }
  for(n=1;n<pr;n++){
       printf("%d",result[n]);
  }
  printf("\n");
  free(a);
  free(b);
  free(result);
}

世界杯比赛日程安排

四年一度的世界杯，在初赛阶段采用循环制，设共有n个队参加，初赛共进行n-1天，每队要和其他各队进行一场比赛，然后按照最后积分选拔进入决赛的球队。要求每队每天只能进行一场比赛，并不能轮空。请按照上述需求安排比赛日程，决定每天各队的对手。

算法思想：根据分治法思路，将所有参赛队伍分为两半，则n个队的比赛日程表可以通过n/2个队的比赛日程来决定。然后继续按上述一分为二的方法对参赛队进行划分，直到只剩余最后2队时为止。

假设n个队的编号为1，2，3，....n,将比赛日程表制作成一个二维表格，每行表示每个队每天所对阵的编号。例如8支球队7天比死哎的日程表如下。

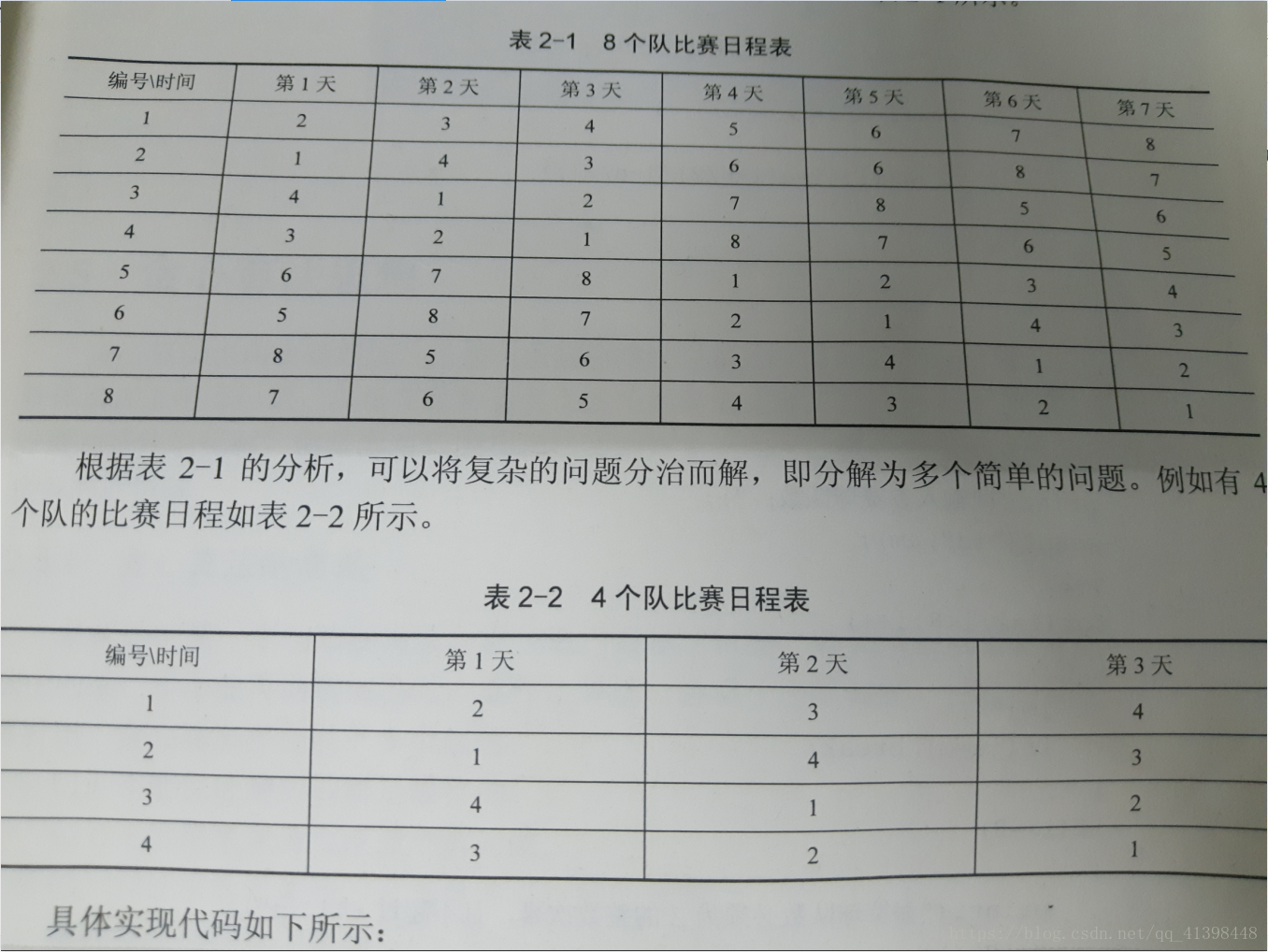
#include<stdio.h>  
#define MAXN 64  
int a[MAXN+1][MAXN+1]={0};  
void gamecal(int k,int n)//处理编号k开始的n个球队的日程  
{  
    int i,j;  
    if(n==2){  
       a[k][1]=k;  //参赛球队编号  
       a[k][2]=k+1;  //对阵球队编号  
       a[k+1][1]=k+1; //参赛球队编号  
       a[k+1][2]=k;  //对阵球队编号  
    }  
    else{  
       gamecal(k,n/2);  
       gamecal(k+n/2,n/2);  
       for(i=k;i<k+n;i++){ //填充右上角  
           for(j=n/2+1;j<=n;j++){  
              a[i][j]=a[i+n/2][j-n/2];  
           }  
       }  
       for(i=k+n/2;i<k+n;i++){  //填充左下角  
            for(j=n/2+1;j<=n;j++){  
               a[i][j]=a[i-n/2][j-n/2];  
            }  
       }  
    }  
}  
void main()  
{  
  int m,i,j;  
  printf("输入参赛球队数:");  
  scanf("%d",&m);  
  j=2;  
  for(i=2;i<8;i++){  
      j=j*2;  
      if(j==m){  
        break;  
      }  
  }  
  if(i>=8){  
     printf("参赛球队数必须为2的整数次幂,且不超过64！\n");  
     getchar();  
  }  
  gamecal(1,m);  
  printf("\n球队编号 ");  
  for(i=2;i<=m;i++){  
        printf("%2d天",i-1);  
  }  
  printf("\n");  
  for(i=1;i<=m;i++){  
        for(j=1;j<=m;j++){  
            printf("%5d ",a[i][j]);    
        }  
		    printf("\n");
  }  
  getchar();  
}