一、隐马尔科夫模型的基本概念
1、马尔可夫链:时刻t+1下状态的概率分布只与时刻t下状态有关,与该时刻以前的状态无关。
数学公式表达: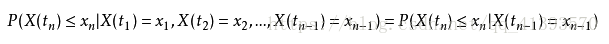
图形表示: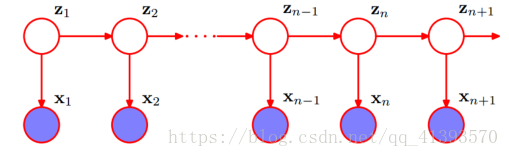
2、隐马尔可夫模型:状态(z)不可直接观测的马尔可夫链。
HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定。
![]()
![]() 描述整个隐码模型。
描述整个隐码模型。
3、隐马尔科夫模型的3个基本问题
1、概率计算问题。知道HMM的参数 λ = (A, B, π) 和观测序列O = {o1,o2, ..., oT} ,如何计算模型 λ 下观测序列O出现的概率P(O | λ)。
2、学习问题。已知观测序列O = {o1,o2, ..., oT} ,估计模型λ = (A, B, π)参数。使得在该模型下观测序列概率P(O | λ)最大。即用极大似然估计的方法估计参数。
3、预测问题。已知模型λ = (A, B, π)和观测序列O = {o1,o2, ..., oT} ,求对给定观测序列条件概率P(I | λ)最大的状体序列I=(i1,i2,...,iT)。即给定观测序列,求最有可能的对应的状态序列。
二、概率计算算法
2.1直接算法
穷举法所有的状态序列(i1,i2,..,it只是一组变量)

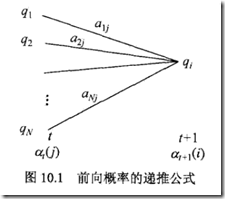
2.2前向算法
前向算法,其实就是定义一个递归算法,即用上一层的前向概率来计算当前的前向概率
看看下图,
如果穷举,3的3次方,计算27次,因为对于这个case,长度为3的隐藏状态序列的可能性为27
而如果用前向算法,需要计算3×3 + 3×3 = 18次,因为它避免了重复计算
前向算法的核心思路,就是避免重复计算,其实是一种动态规划算法
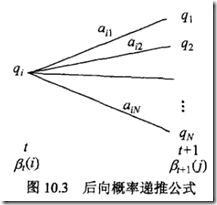
2.3 后向算法
定义后向概率,当t时刻的状态为![]() ,那么
,那么![]() 的概率,就为后向概率
的概率,就为后向概率
后向算法,
首先初始化,对于T时刻的状态,没有后续状态,所以后向概率默认设为1
接着给出递推公式,可以反向推出前一层的后向概率,求到第一层的时候,把所有状态的后向概率求和就得到![]()
三、学习算法
3.1监督学习算法
那么直接用极大似然来拟合参数,即直接统计
即在i状态转移到j状态的次数除以从i状态转移的总数
这个方法很简单,但是问题是训练集是很难获取的
所以实际用到的都是无监督算法
3.2 无监督算法,Baum-Welch算法
这就是含有隐变量的概率模型,
求解这种问题的典型算法是EM算法,具体算法这里不列,后面有空再细看
四、预测问题
4.1近似算法
找出对于观测状态序列,在每个时刻t,最有可能出现的隐藏状态![]() , 从而得到
, 从而得到![]()
并且有前向,后向概率定义可知
所以,只需求得,
这个算法计算简单,但不能保证预测的状态序列整体上是最有可能的状态序列
4.2 Viterbi 算法
其实就是用动态规划算法来求解最优路径
预测问题是隐马尔可夫比较重要的问题和常见的问题,因为用隐马尔可夫往往就是为了同观测状态去挖掘隐藏状态
比如上面通过房子中的植物状态去推测天气的状态
或者自然语言处理中,去推测每个词的词性
动态规划算法,关键就是写出递归式,
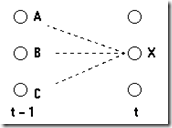
如果我知道到t-1时刻到3个状态A,B,C的最优路径
那么如果要找到到x节点的最优路径,很简单,从A+AX,B+BX,C+CX这3个路径中找到个最优的即可
形式化的表示,
定义,
在t时刻,到达状态i的所有路径中,最优路径的概率;最优路径即概率最大的路径
于是得到递归式,
t时刻每个状态的最佳路径概率值×迁移到i状态的概率×i状态得到观测值Ot+1的概率,求其最大值
得到t+1时刻,最优路径的概率
当到T时刻,找到所有状态节点的最优路径中,概率最大的,就是全局最优路径
但此时,只知道最优路径最后的状态是i,过程中的路径需要回溯回去,
所以在求解时,需要buffer每一时刻,每一状态的最优路径的上个节点,即来自上一时刻哪个状态
和求解公式比,少了个b,是因为对于相同i,b是一样的,所以略去
最终,完整的Viterbi算法
参考:https://www.cnblogs.com/fxjwind/p/3949993.html
https://blog.youkuaiyun.com/pipisorry/article/details/50722178
https://blog.youkuaiyun.com/likelet/article/details/7056068
https://blog.youkuaiyun.com/xueyingxue001/article/details/51435752





 本文详细介绍了隐马尔科夫模型的基础概念,包括马尔可夫链、模型参数及三大基本问题,并深入探讨了概率计算算法、学习算法及预测问题的解决方法。
本文详细介绍了隐马尔科夫模型的基础概念,包括马尔可夫链、模型参数及三大基本问题,并深入探讨了概率计算算法、学习算法及预测问题的解决方法。
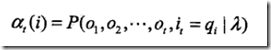
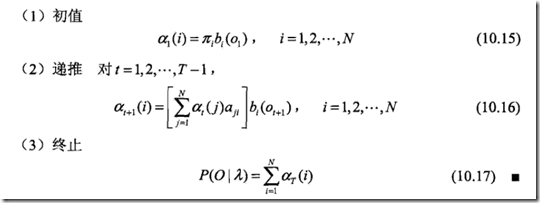
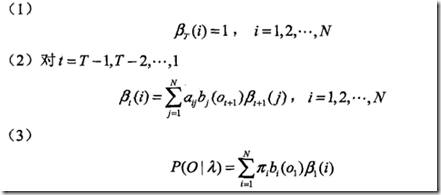
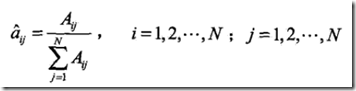
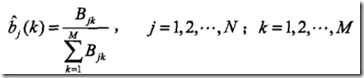
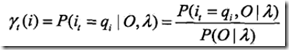
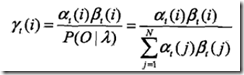
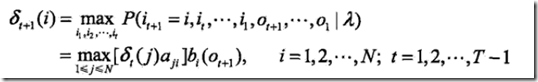

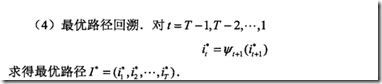
















 3101
3101

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








