四轴无人机的姿态解算（1）

哇我哭了，对imu得到的数据进行姿态结算好像终于能通过去了，记录总结一下。。。

对比了网上搜到的博客、代码和已有的代码，发现既简单又有效的解算方法好像比较固定，因为大家都用的一个程序。。。

1、先从旋转物体的姿态的描述方法开始讲起。

怎么描述一个旋转物体的当前状态呢？其实可以直观的想一下，一个物体的重心位置不变，就假设这个重心被固定在原点，然后整个物体可以绕这个点自由转动。为了直观，可以取一个正方体，设上面的法向量为p，那么对于任意给定的位置，我们只需要使p与该位置的p方向一致，也就是重合，然后绕p旋转，总会与给定位置有重合的时候。也即是说，只要有一个三维向量p，一个角度值（标量，范围0-2pai），给你任何的位置，你都能用这两个量找到表示方法。如果仔细想的话，还可以发现这样表示不光完备，而且唯一。（为什么提到这个，因为欧拉角表示方法并不满足这一点）

比较啰嗦，但这就是四元数的直观理解，即用四个数[a,x,y,z]来表示一个旋转物体的姿态，a是角度，x，y，z表示一个三维向量，但向量既有长度又有方向，我们只需要一个向量来表示方向时，可以规定它是个单位向量。

然而这并不是四元数，真正的四元数定义是这样的：


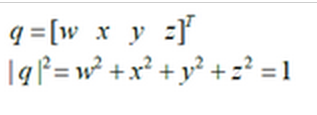
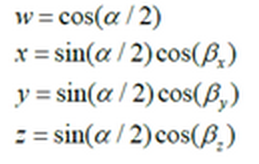
其中是α绕旋转轴旋转的角度，cosβx，cosβy，cosβz为旋转轴在x,y,z方向的分量（由此确定了旋转轴）。而我们先前提到的那个东西是[α，βx，βy，βz]。
为什么这样定义？可能数学原理比较深奥了，目前条件难求甚解。

接下来是用欧拉角表示姿态，即常说的yaw航向角，roll滚转角，pitch俯仰角，这里实际上是理解上的难点。
以一般的想法的话，三个角分别表示方向改变、侧翻和前翻，三个维度的变化都全了，看起来非常直观，为什么说这里难呢。。因为这里的旋转的讲顺序的，打个比方当前无人机的姿态是倾斜的，现在我让它俯仰角加大（相对于固定在无人机上的坐标系），那么对于这个坐标系来讲，只是一个维度的变化，也就是z方向的角度增大，但对于地坐标系，这个运动可就略微有点复杂了，没有办法用一维的变量去描述它。

那么我们如何有效定义欧拉角？

欧拉角有两种定义：
①经典欧拉角（Proper Euler Angle）
z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y
即第一个旋转轴和最后一个旋转轴相同。
②泰特布莱恩角（Tait–Bryan angles）
x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z
三个旋转轴都不同

定义和区别懒得写了，总结的文章有很多可以搜搜看看，一般我们用欧拉角讨论问题的时候，一定会先确定旋转方式，也就是以上12种的一个，对于飞控的话，我们一般是泰特布莱恩角，内旋，方向是xyz或者zxy。

这个东西理解起来的话，主要就是把握一个旋转要有顺序，然后你就会发现这个东西并不好用，至少对于人的思考方式来讲。

还有就是刚提到的，欧拉角表示同一个姿态，表示方法是不唯一的，就导致求解中会出现奇异点，以及大幅度运动会出现的万向节锁，懒得详说，总之就是不得劲。。。

2、然后就是姿态变换矩阵
。。。
这个我也懒得说，实质就是当前一个物坐标系中的向量，可以通过三次线性变换，可以变到地坐标系中，学过线性代数就很容易理解，坐标系的变换而已。由于微分也是线性运算，物坐标系的角速度也就可以以相同的矩阵运算得到地坐标系的角速度。

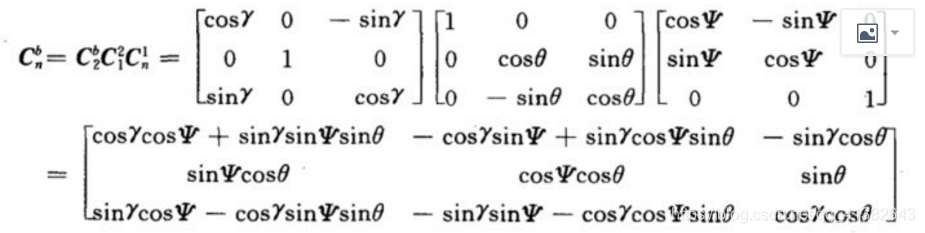
其中三个角度分别为三个欧拉角，也就是说姿态变化矩阵具体的取值由且仅由当前姿态决定，当然如果能得到姿态变换矩阵，也就可以得到当前姿态数据了。
同时我们还知道，四元数和欧拉角都是表示姿态的，是描述一个东西的两种方式，其中必然有转换方式，推导我没看，反正肯定有就对了，公式如下:

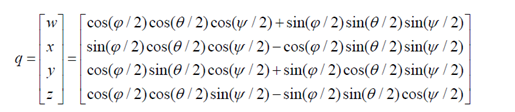
3、当我们在读加速度计和陀螺仪的时候，我们实际在读什么
（更加精准的imu，还要再加一个磁力计，新的无人机里有这东西，orz，估计搞不来，到时候算法会用就行了，也不打算细看。。。。）

看一下mpu6050的源程序，可以发现数据区除温度外有12个八位寄存器，也就是说对于加速度计和陀螺仪的数据，都分别有xyz这三个分量，每个分量对应了一个16位的数据。

陀螺仪可以测角速度，是物坐标系的角速度（划重点），怎么得到角度呢？我们知道是用角速度积分的方法可以得到角度。但具体来讲，并不是直接对测量值进行积分。。。实际上也差不多，只是没有直接积分，而是通过对四元数进行积分，在用四元数求得角度。等下详解一下程序。

加速度计仅仅测量的是重力加速度，在我们的飞行器上，就是对重力加速度g（也就是前面说的静态加速度）的测量和分析，其它瞬间加速度可以忽略。
3轴加速度计输出重力加速度在加速度计所在机体坐标系3个轴上的分量大小，所以通常会归一化处理（程序中会看到的），得到单位向量的三个分量大小。重力加速度的方向和大小是固定的。通过这种关系，可以得到加速度计所在平面与地面的角度关系.只是用来消除累积误差，实际上与角度的最终得出关系不大，等下一起讲。