pandas第七章 缺失数据

本文章为DataWhale组队学习pandas第七章缺失数据的习题解答

练一练

对一个序列以如下规则填充缺失值：如果单独出现的缺失值，就用前后均值填充，如果连续出现的缺失值就不填充，即序列[1, NaN, 3, NaN, NaN]填充后为[1, 2, 3, NaN, NaN]，请利用fillna函数实现。（提示：利用`limit``参数）

s = pd.Series([1, np.nan , 3, np.nan, np.nan])
s

首先利用ffill方法进行前向填充构造一个新序列s1，limit设置为1

s1 = s.fillna(method='ffill',limit=1)
s1

然后再利用bfill方法在对s序列进行后项填充构造新序列s2，limit依旧设置为1。

s2 = s.fillna(method='bfill',limit=1)
s2

最后将得到的两个序列相加进行求平均即可。
为什么能得到结果呢，是因为对于NaN来说，他不管加上什么值还是得NaN。

s_new = (s1+s2)/2
s_new

最后给出总结的函数：

def convert_series(s):
    s1 = s.fillna(method='ffill',limit=1)
    s2 = s.fillna(method='bfill',limit=1)
    return (s1+s2)/2
convert_series(s)   

Ex1：缺失值与类别的相关性检验

数据来源

在数据处理中，含有过多缺失值的列往往会被删除，除非缺失情况与标签强相关。下面有一份关于二分类问题的数据集，其中X_1, X_2为特征变量，y为二分类标签。

df = pd.read_csv('../data/missing_chi.csv')
df.head()

-	X_1	X_2	y
0	NaN	NaN	0
1	NaN	NaN	0
2	NaN	NaN	0
3	43.0	NaN	0
4	NaN	NaN	0

df['y'].value_counts()

从下述结果可以看出这1000条记录中，负例为918个，正例为82个。

0    918
1     82
Name: y, dtype: int64

事实上，有时缺失值出现或者不出现本身就是一种特征，并且在一些场合下可能与标签的正负是相关的。关于缺失出现与否和标签的正负性，在统计学中可以利用卡方检验来断言它们是否存在相关性。按照特征缺失的正例、特征缺失的负例、特征不缺失的正例、特征不缺失的负例，可以分为四种情况，设它们分别对应的样例数为$n_{11},n_{10},n_{01},n_{00}$。假若它们是不相关的，那么特征缺失中正例的理论值，就应该接近于特征缺失总数$\times$总体正例的比例，即：

$$E_{11}=n_{11}\approx (n_{11}+n_{10})\times \frac{n_{11}+n_{01}}{n_{11}+n_{10}+n_{01}+n_{00}}=F_{11}$$

其他的三种情况同理。现将实际值和理论值分别记作$E_{ij},F_{ij}$，那么希望下面的统计量越小越好，即代表实际值接近不相关情况的理论值：

S = ∑ i ∈ { 0 , 1 } ∑ j ∈ { 0 , 1 } ( E i j − F i j ) 2 F i j S = \sum_{i\in \{0,1\}}\sum_{j\in \{0,1\}} \frac{(E_{ij}-F_{ij})^2}{F_{ij}} S=i∈{0,1}∑​j∈{0,1}∑​Fij​(Eij​−Fij​)2​

可以证明上面的统计量近似服从自由度为$1$的卡方分布，即$S\stackrel{\cdot }{\sim }{\chi }^2(1)$。因此，可通过计算$P({\chi }^2(1)>S)$的概率来进行相关性的判别，一般认为当此概率小于$0.05$时缺失情况与标签正负存在相关关系，即不相关条件下的理论值与实际值相差较大。

上面所说的概率即为统计学上关于$2\times 2$列联表检验问题的$p$值， 它可以通过scipy.stats.chi2(S, 1)得到。请根据上面的材料，分别对X_1, X_2列进行检验。

这里用X_1特征进行计算（X_2同理）。

sub_set = df['X_1']
df_notna = df[sub_set.notna()] # X_1特征没有缺失
df_notna

可以看出X_1特征没有缺失的数据共有145条。（也就是E0）

df_na = df[sub_set.isna()] # X_1有缺失
df_na

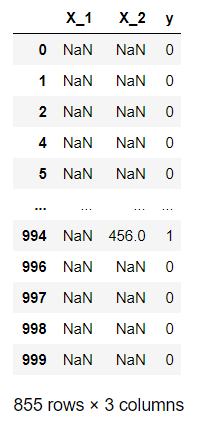
X_1特征缺失的数据共有855条。（145+855=1000）
下面开始求X_1特征缺失的情况下为负例的DataFrame。

df_na_neg = df_na.loc[df_na['y']==0]
df_na_neg

上述得到的就是X_1特征缺失的情况下的负例，它的行数也就是n10(即E10)

n10 = df_na_neg.shape[0]
n10   # ---->785

下面开始求X_1特征缺失的情况下为正例的DataFrame。

df_na_pos = df_na.loc[df_na['y']==1]
df_na_pos

上述得到的就是X_1特征缺失的情况下的正例，它的行数也就是n11(即E11)

n11 = df_na_pos.shape[0]
n11  # --->70

同理计算X_1特征不缺失的情况下的正例与负例。

df_notna_pos = df_notna.loc[df_notna['y']==1]
df_notna_pos

上述得到的就是X_1特征不缺失的情况下的正例，它的行数也就是n01(即E01)

n01 = df_notna_pos.shape[0]
n01   # ---->12

开始求X_1特征不缺失的情况下的负例：

df_notna_neg = df_notna.loc[df_notna['y']==0]
df_notna_neg

上述得到的就是X_1特征不缺失的情况下的负例，它的行数也就是n00(即E00)

n00 = df_notna_neg.shape[0]
n00  # --->133

开始计算 F理论值（下面是特征缺失正例的计算公式，其余同理）

$$E_{11}=n_{11}\approx (n_{11}+n_{10})\times \frac{n_{11}+n_{01}}{n_{11}+n_{10}+n_{01}+n_{00}}=F_{11}$$

E11 = n11  # X_1特征缺失的正例个数
E10 = n10  # X_1特征缺失的负例个数
E01 = n01  # X_1特征不缺失的正例个数
E00 = n00  # X_1特征不缺失的负例个数

total_pos_prop = (n11+n01)/(n11+n10+n01+n00) #总体正例的比例
# 等同于 total_pos_prop = df[df['y']==1].shape[0]/df.shape[0]
total_neg_prop = (n10+n00)/(n11+n10+n01+n00) #总体负例的比例
# 等同于 total_pos_prop = df[df['y']==0].shape[0]/df.shape[0]

定义特征缺失与不缺失的额个数

feat_na_sum = n11+n10  # X_1特征缺失的个数  等同于df_na.shape[0]
feat_na_sum

feat_notna_sum = n01+n00 # X_1特征不缺失的个数 等同于 df_notna.shape[0]
feat_notna_sum

求出相应的理论值

F11 = feat_na_sum * total_pos_prop
F10 = feat_na_sum * total_neg_prop
F01 = feat_notna_sum * total_pos_prop
F00 = feat_notna_sum * total_neg_prop

开始计算统计量：

S = ∑ i ∈ { 0 , 1 } ∑ j ∈ { 0 , 1 } ( E i j − F i j ) 2 F i j S = \sum_{i\in \{0,1\}}\sum_{j\in \{0,1\}} \frac{(E_{ij}-F_{ij})^2}{F_{ij}} S=i∈{0,1}∑​j∈{0,1}∑​Fij​(Eij​−Fij​)2​

S1 = ((E11-F11)**2/F11)+((E10-F10)**2/F10)+((E01-F01)**2/F01)+((E00-F00)**2/F00)
S1

上面所说的概率即为统计学上关于$2\times 2$列联表检验问题的$p$值， 它可以通过scipy.stats.chi2(S, 1)得到。

导入chi2包进行p-value计算

from scipy.stats import chi2
chi2.sf(S1, 1)

0.9712760884395901

一般认为当此概率小于 0.05 时缺失情况与标签正负存在相关关系，即不相关条件下的理论值与实际值相差较大。
所以结论就是X_1特征与标签y不相关。（X_2计算同理）

Ex2：用回归模型解决分类问题

KNN是一种监督式学习模型，既可以解决回归问题，又可以解决分类问题。对于分类变量，利用KNN分类模型可以实现其缺失值的插补，思路是度量缺失样本的特征与所有其他样本特征的距离，当给定了模型参数n_neighbors=n时，计算离该样本距离最近的 𝑛 个样本点中最多的那个类别，并把这个类别作为该样本的缺失预测类别，具体如下图所示，未知的类别被预测为黄色：

df = pd.read_excel('../data/color.xlsx')
df.head(3)

-	X1	X2	Color
0	-2.5	2.8	Blue
1	-1.5	1.8	Blue
2	-0.8	2.8	Blue

已知待预测的样本点为 𝑋1=0.8,𝑋2=−0.2 ，那么预测类别可以如下写出：

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=6)
clf.fit(df.iloc[:,:2], df.Color)
clf.predict([[0.8, -0.2]])

预测结果如下：

array(['Yellow'], dtype=object)

1.对于回归问题而言，需要得到的是一个具体的数值，因此预测值由最近的 𝑛 个样本对应的平均值获得。请把上面的这个分类问题转化为回归问题，仅使用KNeighborsRegressor来完成上述的KNeighborsClassifier功能。

首先将标签color转为one_hot编码形式

label_one_hot = pd.get_dummies(df.Color)  # get_dummies 是利用pandas实现one hot encode的方式。
label_one_hot.head()

-	Blue	Green	Yellow
0	1	0	0
1	1	0	0
2	1	0	0
3	1	0	0
4	1	0	0

from sklearn.neighbors import KNeighborsRegressor # 导入KNeighborsRegressor包

reg = KNeighborsRegressor(n_neighbors=6)
reg.fit(df.iloc[:,:2], label_one_hot)

label_one_hot.columns.tolist()[np.argmax(reg.predict([[0.8, -0.2]]))]

预测结果如下：

'Yellow'

对于上述代码所用的函数进行简要解释：
np.argmax() :这个函数返回是索引，argmax返回最大数的索引。

reg.predict([[0.8, -0.2]])

array([[0.16666667, 0.33333333, 0.5       ]])

a = np.array([0.16666667, 0.33333333, 0.5       ])
np.argmax(a)

2

要获取DataFrame的列名，通过tolist()转换成列表形式：

label_one_hot.columns.tolist()

['Blue', 'Green', 'Yellow']

2.请根据第1问中的方法，对audit数据集中的Employment变量进行缺失值插补。

df = pd.read_csv('../data/audit.csv')
df.head(3)

对原数据做预处理 , 将数值型数据进行min-max归一化 , 类别性数据进行one-hot编码 , Employment作为标签Y放到最后一列:

df_pre = pd.concat([pd.get_dummies(df[['Marital', 'Gender']]),
                    df[['Age','Income','Hours']].apply(lambda x:(x-x.min())/(x.max()-x.min())),
                    df.Employment],1)

划分训练集与测试集 , 筛选出Employment非NaN的行作为训练集 , NaN的行作为测试集

X_train = df_pre[df_pre.Employment.notna()]
X_test = df_pre[df_pre.Employment.isna()]
X_train

训练集展示如下：

Marital_Absent	Marital_Divorced	Marital_Married	Marital_Married-spouse-absent	Marital_Unmarried	Marital_Widowed	Gender_Female	Gender_Male	Age	Income	Hours	Employment
0	0	0	0	0	1	0	1	0	0.287671	0.168997	0.724490
1	1	0	0	0	0	0	0	1	0.246575	0.148735	0.295918
2	0	1	0	0	0	0	0	1	0.205479	0.320539	0.397959
3	0	0	1	0	0	0	0	1	0.383562	0.056453	0.551020
4	0	0	1	0	0	0	0	1	0.589041	0.014477	0.397959
…	…	…	…	…	…	…	…	…	…	…	…
1995	0	0	1	0	0	0	0	1	0.616438	0.048832	0.397959
1996	0	0	1	0	0	0	0	1	0.246575	0.118356	0.397959
1997	0	0	1	0	0	0	0	1	0.205479	0.062267	0.438776
1998	0	0	0	0	1	0	0	1	0.232877	0.234715	0.448980
1999	1	0	0	0	0	0	1	0	0.123288	0.289972	0.346939

将Employment标签转为one_hot形式：

label_one_hot = pd.get_dummies(X_train.Employment)
label_one_hot 

利用KNeighborsRegressor进行训练：

reg = KNeighborsRegressor(n_neighbors=6)
reg.fit(X_train.iloc[:, :-1], label_one_hot)

在测试集X_test上进行预测：

a = reg.predict(X_test.iloc[:, :-1])
a

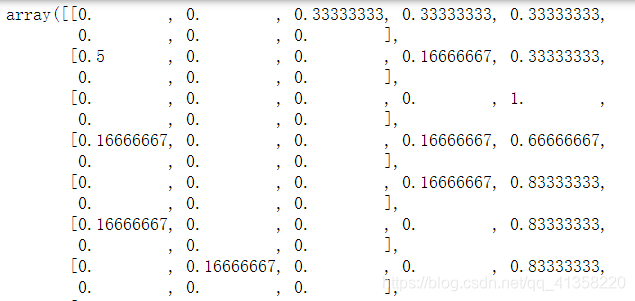
预测结果部分展示如上。可以看到是一个二维数组，每一条数据所属Employment类别概率如图。

a.shape  # -->（100，8）Employment一共有八个类别

predict_res = []
for i in range(a.shape[0]):
    predict_res.append(np.argmax(a[i]))
predict_res[:5]

[2, 0, 4, 4, 4]

从上述结果可以看出对于测试集上前五条数据他们所属的Employment类别索引分别为【2，0，4，4，4】，对应的职位即为【PSLocal，Consultant，Private，Private，Private】

label_one_hot.columns.tolist()

final_res = []
for i in predict_res:
    final_res.append(label_one_hot.columns.tolist()[i])
final_res[:5]

展示结果如下：

['PSLocal', 'Consultant', 'Private', 'Private', 'Private']

最终，df中Employment为NaN的替换为final_res即可：

df.loc[df.Employment.isna(), 'Employment'] = final_res

验证df的Employment列是否有空值：

df.Employment.notna().all()

True

结果显示没有空值。