裁剪算法——Cohen-Sutherland算法

一、直线裁剪算法

1、裁剪：计算机内部存储的图形往往比较大，而屏幕显示的只是图形的一部分，因此需要确定图形哪些部分落在显示区之内，哪些落在显示区之外，这个选择的过程就称为裁剪。

1.1点的裁剪——>此方法太费时，效率比较低，一般不可取。

对于任意一点P(x,y)若满足下列不等式，则点P在矩形窗口内

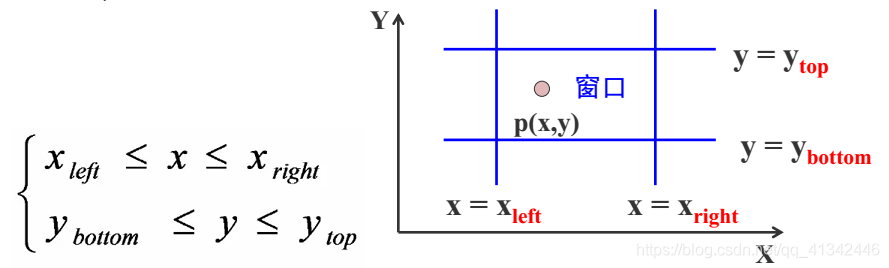
1.2直线段的裁剪——>复杂图形裁剪的基础

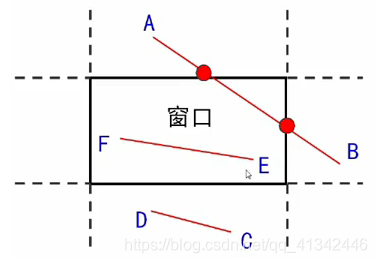
要裁剪一条直线段，首先要判断此直线的位置：
1)它是否完全落在裁剪窗口内？
2)它是否完全在窗口外？
3)如果不满足以上两个条件，则计算它与一个或多个裁剪边界的交点。

二、Cohen-Sutherland算法(编码裁剪算法)

首先对直线段的端点进行编码。

基本思想：对每条直线段分三种情况处理：
1）若点p1和p2完全在裁剪窗口内——>“简取”之（保留这条直线）

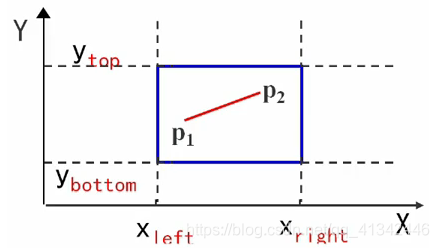
2）若点p1(x1,y1),p2(x2,y2)均在窗口外，且满足下列四个条件之一：——>“简弃”之（不要了）

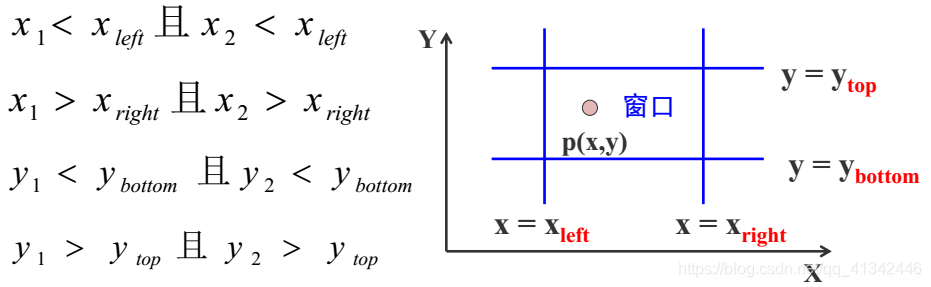
3）如果直线段既不满足“简取”的条件，也不满足“简弃”的条件？
——>需要对直线段按交点进行分段，分段后判断直线是“简取”还是“简弃”。

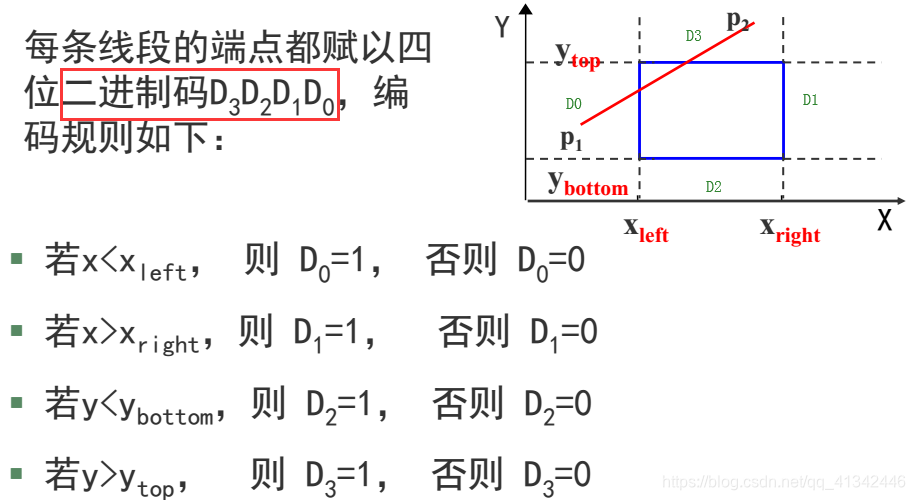
裁剪一条线段时，先求出端点p1和p2的编码code1和code2，然后进行二进制“或”运算和“与”运算。

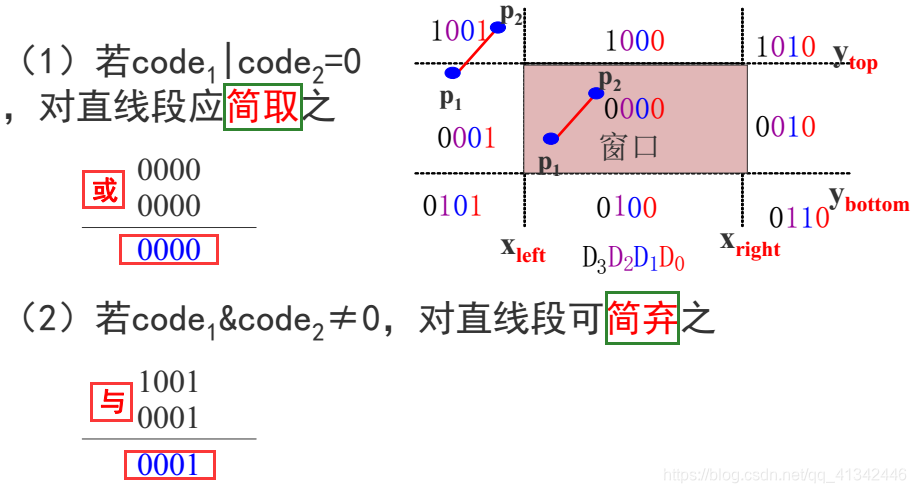
注：【若这两个条件均不成立，则需要求出直线段与窗口边界的交点在交点处把线段一分为二。】

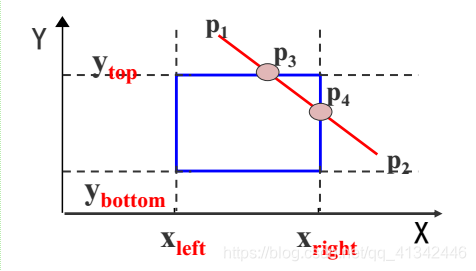
如裁剪如下图所示的直线段P1P2：

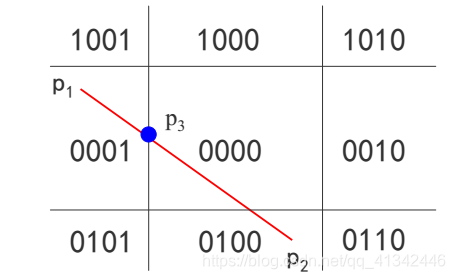
首先对P1P2进行编码

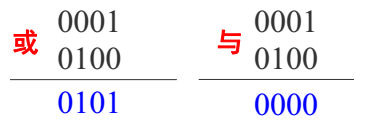
令直线段与窗口左边界的交点为P3，
则可知P1P3必在窗口外，可以简弃之。

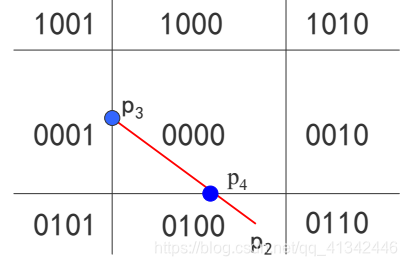
再令直线段与窗口下边界的交点为P4，

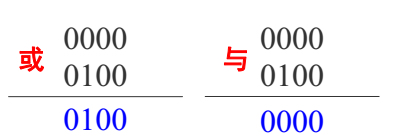
剩下的直线段（P3P4）再进行进一步判断，code1|code2=0,全在窗口中，简取之
【点P在窗口边界也属于在窗口内】
【存在的问题】

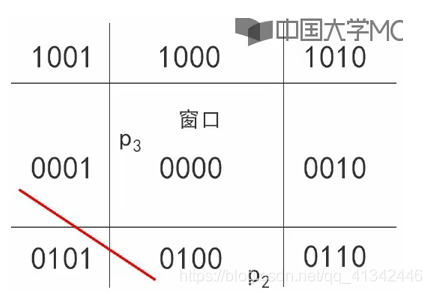
如图中线段全部在窗口外部，但是对两段端点进行或/与运算时，需要再次取交点进行运算，最坏情况下，被裁剪线段与窗口4条边计算交点，然后所得的裁剪结果却可能是全部舍弃。

【小结】Cohen-Sutherland算法比较适合两种情况：
1、大部分线段完全可见；
2、大部分线段完全不可见。

转载连接：https://www.cnblogs.com/Penglimei/p/9690372.html