剑指 Offer 37 序列化二叉树、字符串的全排列、正则表达式匹配（难）

剑指 Offer 37. 序列化二叉树

你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

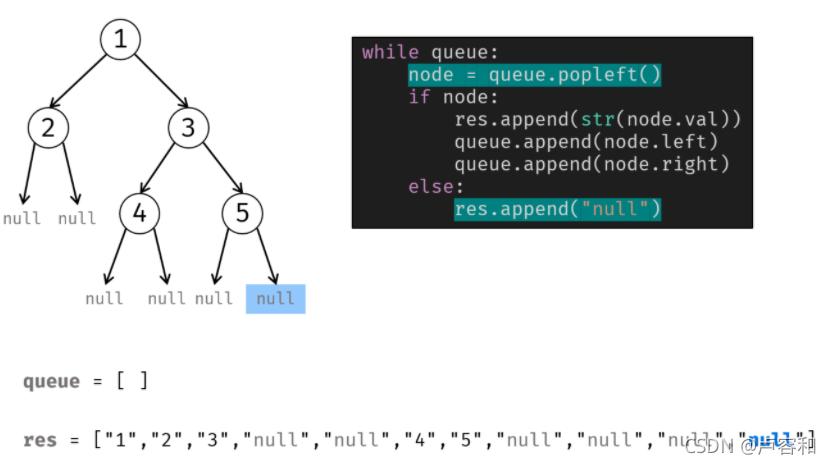
这个不难，只是把空节点也放入队列。

反序列化，可根据计算公式，如果他是完全二叉树，索引从1开始，我们是知道父节点索引为x，则左儿子是2x，右儿子为2x+1。

这里索引从0开始。公式就有一点不同。父亲索引x，左儿子2x+1，右儿子2x+2

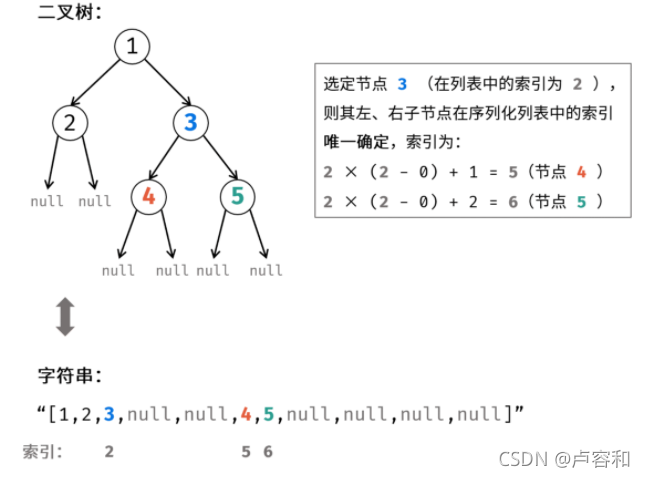
上图公式就是说，父亲之前有多少个空节点，它的儿子将在原本的排序减去空节点的两个不存在的儿子（null）。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
from collections import deque
class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        if not root: return "[]"
        queue = deque()
        queue.append(root)
        res = []
        while queue:
            node = queue.popleft() # 非空节点都会存它的儿子,不管是否空节点
            if node:
                queue.append(node.left)
                queue.append(node.right)
                res.append(node.val)
            else:
                res.append("null")
        return str(res)

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """
        if data == "[]": return None
        res, i = eval(data), 1 # 非空节点都会存它的儿子,不管是否空节点
        root = TreeNode(int(res[0]))
        queue = collections.deque()
        queue.append(root) # 只记录非空节点
        while queue:
            node = queue.popleft() 
            if res[i] != "null":
                node.left = TreeNode(int(res[i]))
                queue.append(node.left)
            i += 1
            if res[i] != "null":
                node.right = TreeNode(int(res[i]))
                queue.append(node.right)
            i += 1
        return root



# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.deserialize(codec.serialize(root))

剑指 Offer 38. 字符串的排列

输入一个字符串，打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

算法书里面常见的题目：
输入：s = “abc”
输出：[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]

分：字符互不重复 和 存在重复字符。

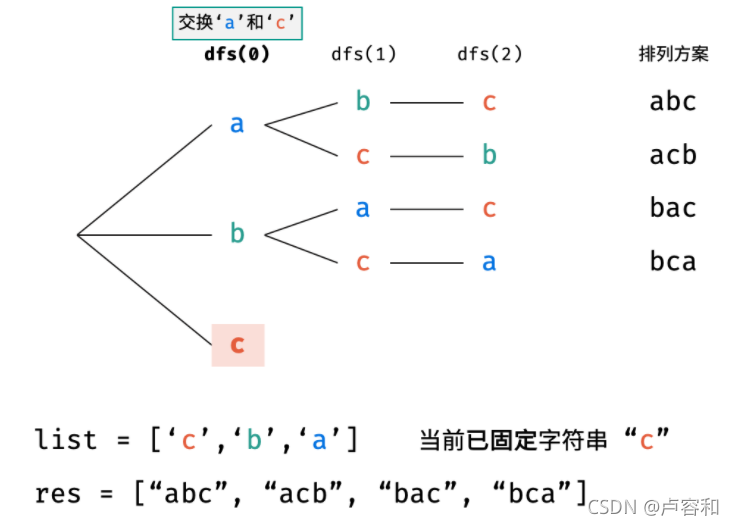
>>> a = "abc"
>>> b = list(a)
>>> b
['a', 'b', 'c']
>>> c = ''.join(b)
>>> c
'abc'

class Solution:
    def permutation(self, s: str) -> List[str]:
        def dfs(i):
            if i == self.num - 1:
                res.append(''.join(c))
                return
            past = set()
            for x in range(i, self.num):
                if c[x] in past: continue # 重复，因此剪枝
                past.add(c[x])
                c[i], c[x] = c[x], c[i]  # 交换，将 c[x] 固定在第 i 位
                dfs(i + 1)               # 开启固定第 i + 1 位字符
                c[i], c[x] = c[x], c[i]  # 恢复交换
        
        c, res = list(s), []
        self.num = len(c)
        dfs(0)
        return res

剑指 Offer 19. 正则表达式匹配

请实现一个函数用来匹配包含 ’ . ’ 和 ’ * '的正则表达式。模式中的字符 ’ . ’ 表示任意一个字符，而 ’ * ’ 表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与式 "a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

怎么与动态规划联系，转移方程？

应该利用*和.的功能，如果两个位置不相同相同时，两个长度不相同时，

当p【j-1】不为 ‘ * ’，只能看左上角的，即要用新的p和s比较
当p【j-1】为 ‘ * ’，功能：

1. 忽略前一个
2. 重复，使的s多一个也能应付
3. 重复，使的s多一个也能应付，但重复的是‘.’， 条件可以放宽
   

黄色部分难绕：dp【i-1】【j】，带表s【i-2】与p【j-1】匹配了，且p【j-1】为 * ，所以s【i-2】在多一个s【i-1】如果与 * 号前的p【j-2】相同，则*号可以重复一次前面的，使dp【i】【j】也可以。

你可能想，*号可以重复多次的功能在哪里体现呢？
dp【i】【j】由dp【i-1】【j】得到，那么它也可以由dp【i-2】【j】得到，dp【i-3】【j】得到，这时说明p【j-1】这个 * 号，已经重复了3次前一个数p【j-2】

注意dp中的ij和字符串的位置。

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        m, n = len(s) + 1, len(p) + 1
        dp = [[False] * n for _ in range(m)]
        dp[0][0] = True
        # 初始化首行
        for j in range(2, n, 2): # 偶数位置为*, 看前两个位置
            dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
        # 状态转移
        for i in range(1, m):
            for j in range(1, n):
                if p[j - 1] == '*':
                    if dp[i][j - 2]: dp[i][j] = True                              # 1.
                    elif dp[i - 1][j] and s[i - 1] == p[j - 2]: dp[i][j] = True   # 2.
                    elif dp[i - 1][j] and p[j - 2] == '.': dp[i][j] = True        # 3.
                else:
                    if dp[i - 1][j - 1] and s[i - 1] == p[j - 1]: dp[i][j] = True # 1.
                    elif dp[i - 1][j - 1] and p[j - 1] == '.': dp[i][j] = True    # 2.
        return dp[-1][-1]

又是cv工程，不过这题属于动态规划，一定要练会。