贪心Greedy2

一 数据结构

1 BST&BBST

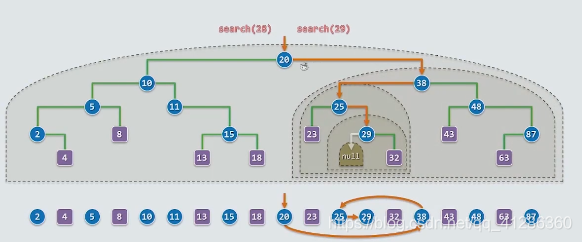
二叉搜索树BST
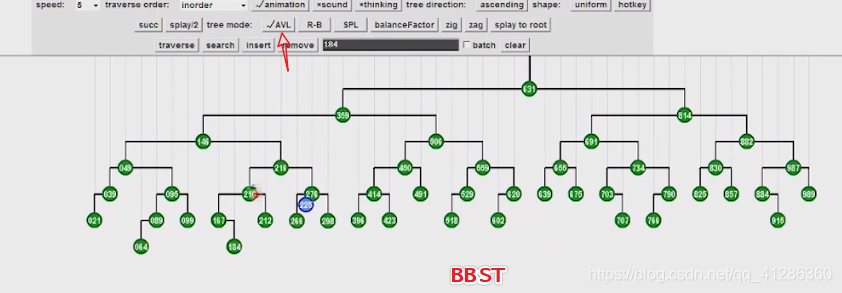
平衡二叉搜索树BBST
BBST是BST的优化

2 Hashtable+Dictionary+Map

这种数据组织方式，可以在常数时间内找到想要的数值

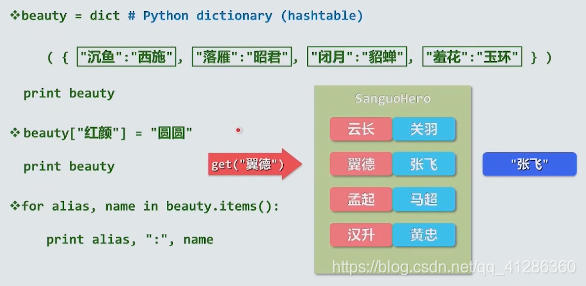
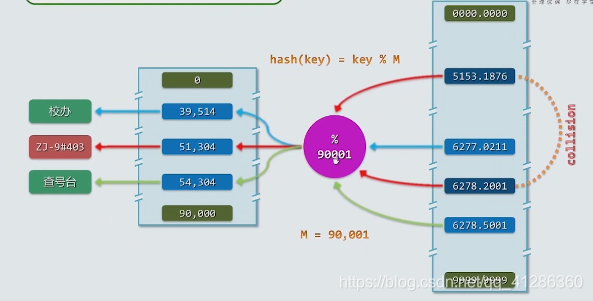
散列表的存储结构:

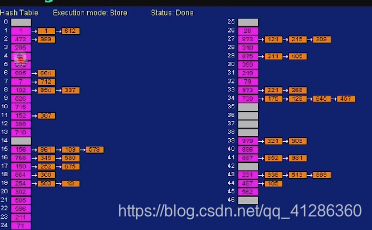
散列表的映射

3 Priority Queue

上节课中的Huffman tree
如果用vector存储数据
取出两颗，合并，并插进去，要n-1次迭代
每次找两颗最小的树，要从中遍历一遍，需要n
复杂度O(n(n-1))–>O(n^2)

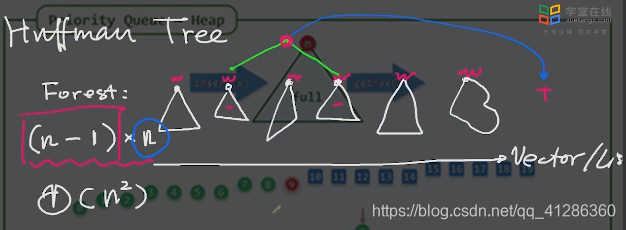
如果采用堆，O(nlog(n))
底数是2.
换地公式：logan~logab*logbn
两边加bigO后logab就是个常数，就可以省略；所以其底就没有意义了；在bigO中其实就就可以不写；

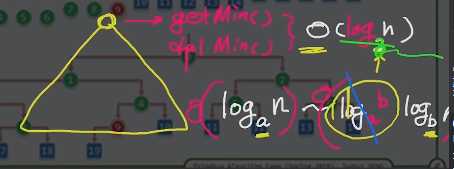
堆属于优先级队列中的其中一种数据结构，这是一个大家族；

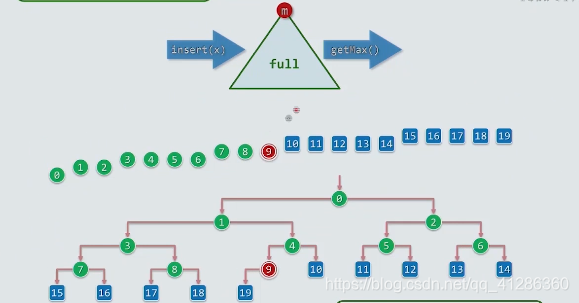
除了用堆以外，还有其他的方法也可以实现O(nlogn)
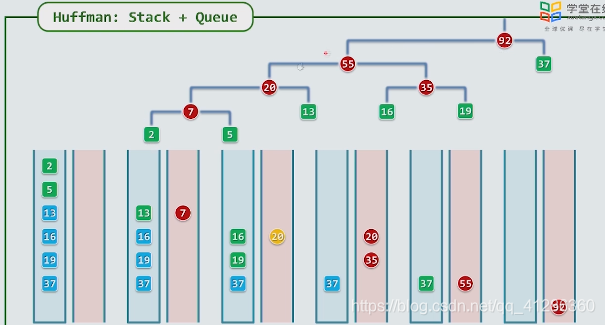
栈+队列（姊妹）
最多同时考虑栈四个元素；堆中或者栈中的各两个元素
先对元素排序，然后放到栈中，
队列中放从栈中取出的两个元素的和
在队列中最多会放两个元素；
后面就是不断的从队列和栈中选择最小的值。每次都是在>4的常数内选取元素。所以是在 线性的时间内做的事情；

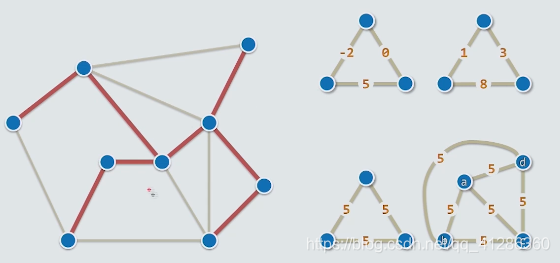
二 Minimum Spanning Tree

图中任何两个点都是可以到达的；
最小生成树是以上方案中的最优方案；

1 prim：cut+Cross

cut:割
Cross：跨越边
最小支撑树总会采用连接每一割的最短跨越边

如下：U和V/U两个割，其中4，6，7为其中的两个割的cross，4是最短的cross；

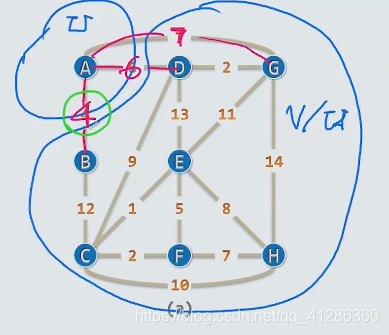
所以采用4的cross

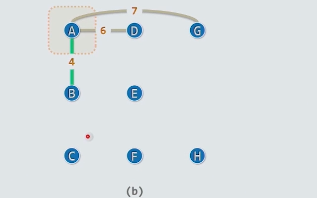
2最小，所以采用2，G进U中来；

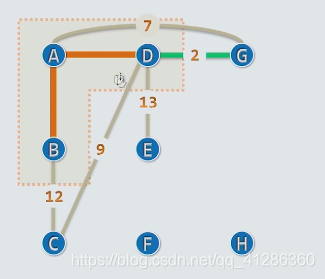
U不断的扩大，贪心策略最后得到下面的最小支撑数：

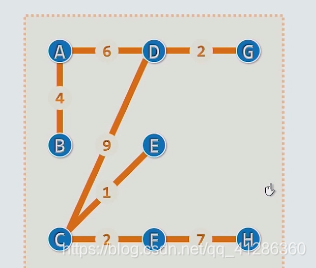
演示如图：

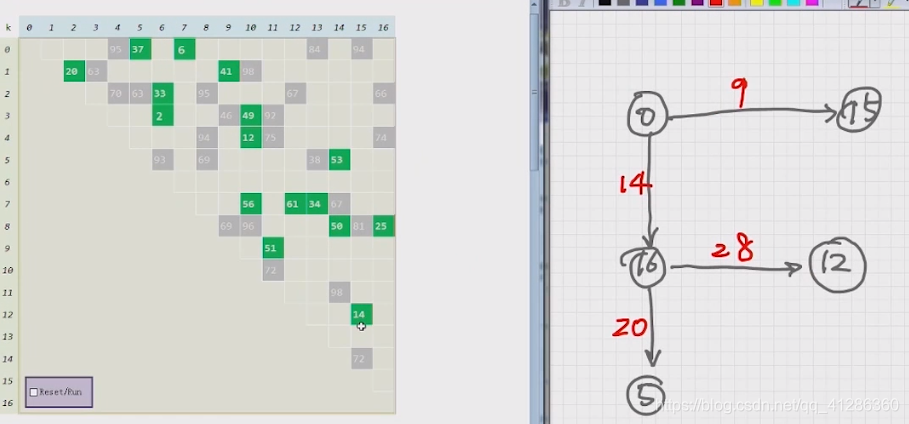
prim算法的实现：
采用的数据结构是堆；
初始状态：

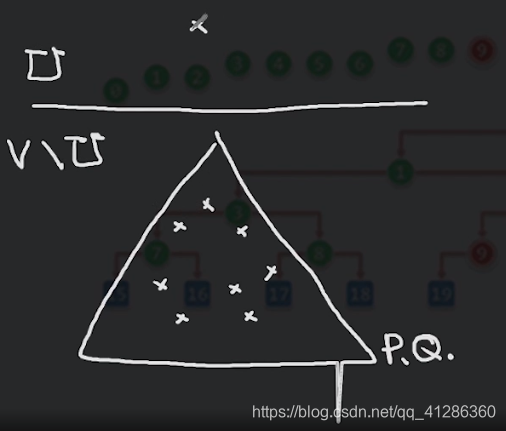
找到下图中最短的跨边
下面的每个点都让它自己记录个数，
记录它自己拥有的 权重，这个权重其实就可以看成是上面的点到下面的点的distance，
dist(v)=min{|v,u|,u∈U}
用delmin()直接取出这些距离中的最小值，

复杂度是O(nlogn)

2 Kruskal :sorting by weight

先按权重将边进行排序，
然后做个线性扫描
第1，2条边不用考虑，肯定直接加进来，但是第三条边需要满足一定的条件才可以；

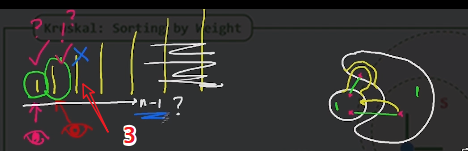
为啥第三条边为啥加不能加？
如下图，当第三条边加进来的时候，如果如图所示，第1，2加进来的时候，第三条边的两端已经在U内部了；第三条边构成了环路，
随着第4，5条边风险会越来越大

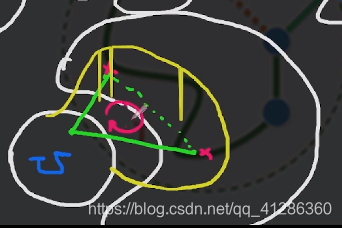
可以加进来的条件是：判断两个点是否在同一棵树上，
不在同一棵树，在可以，在同一棵树则不可以；

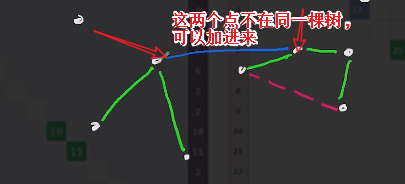
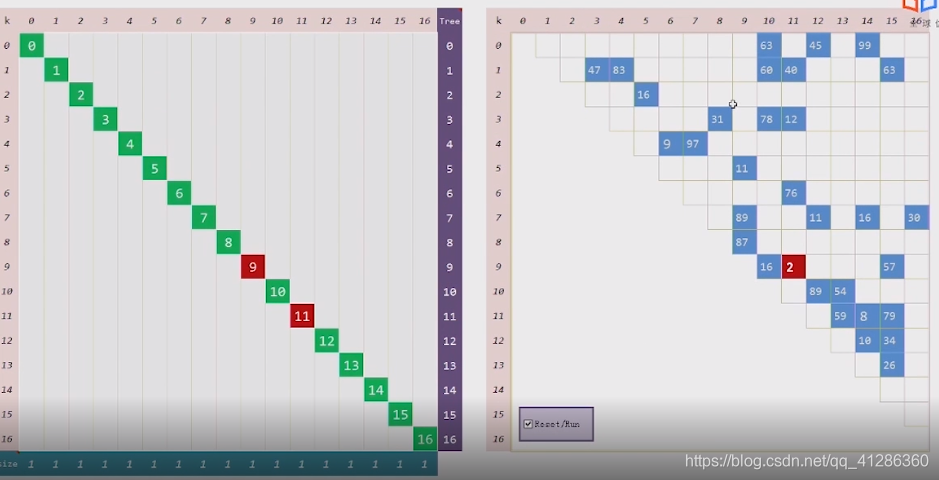
算法的实现：