05.二叉搜索树（一）

05.二叉搜索树（一）

• 二叉搜索树也被称为：二叉查找树、二叉排序树

  定义：

  • 任意一个节点的值都大于其左子树所有节点的值。
  • 任意一个节点的值都小于其右子树所有节点的值。
  • 它的左右子树也是一颗二叉排序树
    • 总结来说：比我小的往左拐，比我大的往右拐。

• 特点：

  • 二叉搜索树存储的元素必须具备可比较性（比如int、double等）
  • 如果不是自定义类型，需要指定比较方式

• 优点：

  • 可以大大提高搜索数据的效率

  二叉搜索树没有索引的概念

• 这是为什么呢？我们不是可以按照从上到下，从左到右，进行编号吗？例如下图：

• 但是这样不对，没有意义，比如，我们再一个添加，11,15的元素进来，按照二叉排序树，11 > 8 —> 往右子树走，11 > 10 —> 在往右走，11 < 14 —> 往左走，11 < 13 —>往左走，发现没有元素，插入该位置，15也是一样，那么得出来的结果应该是：

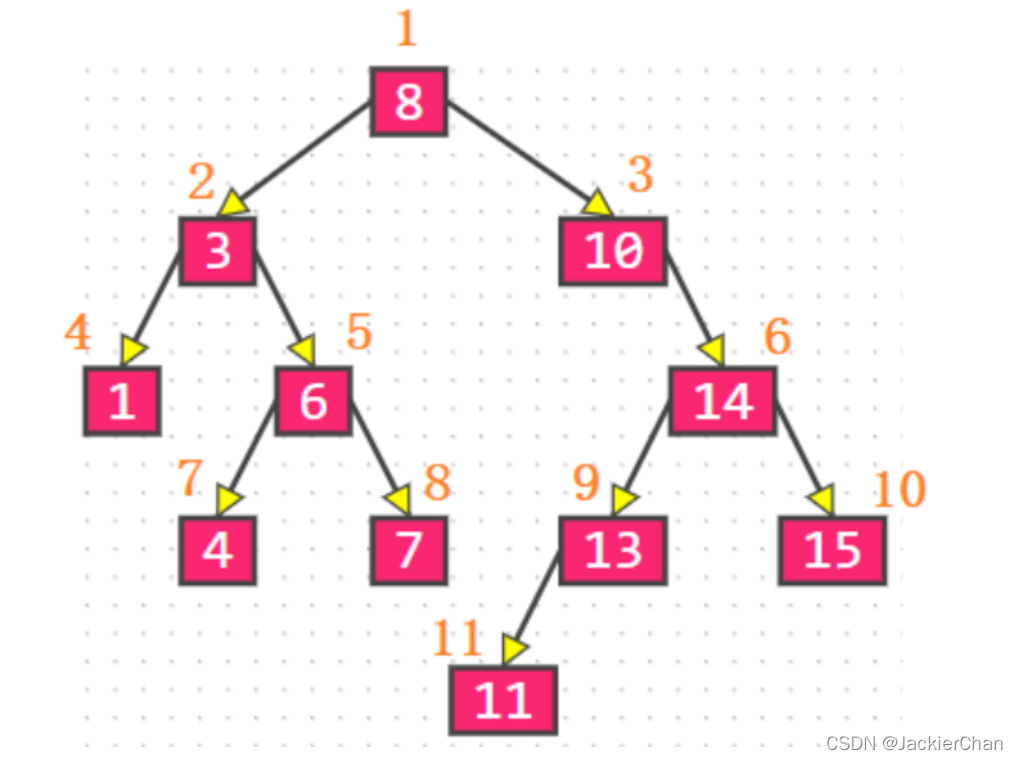
这样的编号索引与我们之前数组与链表的先入先编号是不一样，所以在二叉搜索树中没有索引的概念。

平衡二叉树的add方法

• 重点:

  • 步骤：
    • 1.找到父节点parent
    • 2.创建新节点node
    • 3.找到父节点并记录插入父节点的方向parent.left = node或parent.right = node
    • 如插入的值相等直接return，不作处理。

• 为了确保添加的元素必须具备可比较性，对添加的元素不能为null，所以需要对添加的元素进行非空检查。

 public void elementNotNullCheck(E element){
        if (element == null){
            //非法参数异常
            throw new IllegalArgumentException("element must not is null");
        }
    }

• 下面需要做的就是找到父节点。遍历查找父节点时，如果树为空树，不用查找。添加的节点就是根节点。若不为空树，我们需要从根节点开始遍历。

  • 这是我们重点分析的地方
  • 由于二叉搜索树具备可比较性，我们定义一个比较方法来比较两个元素的大小

  /**
   * 比较函数，返回0，e1==e2;返回值大于0，e1>e2;返回小于0，e1<e2
   * @param e1
   * @param e2
   * @return
   */
  private int compare(E e1,E e2){
  	return 0;
  }
  

  • 这里的逻辑我们先不写，因为我们设计的二叉树在设计上是支持泛型的，对于java官方提供的基本数据类型，例如：int、double或者是String类型，这种基本的数值类型的比较逻辑是比较好写的,但是对于类类型来说，例如Person类，这是不行的，因为我们不知道比较规则。

    public class BinarySearchTree<E> {
        //...
    }
    

    public class Person {
    
        /**
         * 年龄
         */
        private int age;
    
        public Person(int age) {
            this.age = age;
        }
    }
    

• 针对上面说到的缺点，我们可以通过以下方法解决：

  1.强制要求实现java.lang.Comparable接口，重写public int compareTo(T o);方法，自定义比较规则

  public class BinarySearchTree<E extends Comparable<E>>{
      //泛型E必须实现Comparable接口
  }
  

  例如：Person 类

  public class Person implements Comparable<Person> {
      private int age;
  
      public Person(int age){
          this.age = age;
      }
      /**
       * 自定义比较规则:
       * 以年纪作为比较大小
       * @param p
       * @return
       */
      @Override
      public int compareTo(Person p) {
          return age - p.age;
      }
  }
  

  这样子就可以在BinarySearchTree二叉搜索树种的compare方法中调用重写的compareTo方法，实现比较逻辑，但是这样写有一些不好的地方，比如说对于传入的类型进行了强制要求，同时，由于比较规则是编写在Person类中的，对于一个类来说只能自定一种比较规则，很不方便。

  2.编写java.util.Comparator接口的匿名内部类，重写int compara(T O1 , T O2);方法

  • 同时在BinarySearchTree类中，添加接收用户自定义比较器的属性，这样做到可以实现按照自定义规则，编写不同的比较器

    //接收用户自定义比较器
    private Comparator<E> comparator;
    
    /**
     * 构造函数
     * @param comparator
     */
    public BinarySearchTree2(Comparator comparator) {
        this.comparator = comparator;
    }
    

    这时候，只需要在实例化二叉搜索树时，传入比较器就行，例如：

     BinarySearchTree<Person> bst2 = new BinarySearchTree(new Comparator<Person>() {
         		//自定义比较规则
                @Override
                public int compare(Person p1, Person p2) {
                    return p1.getAge() - p2.getAge();
                }
            });
    

    但是，这样子还是不好，因为在实例化时，如果没有传入比较器，编译器监测就会报错，那么就有了第3种方法。

    • 我想做到不管用户传没传比较器，我都能提供接口对其比较大小。

  3.保留Comparable和Comparator接口，同时提供无参构造，与有参构造

  //无参构造   
  public BinarySearchTree(){
          this(null);//调用有参构造方法
      }
  //有参构造
      public BinarySearchTree(Comparator<E> comparator){
          this.comparator = comparator;
      }
  

• 这样的话，如果用户有传入比较器的话，就用比较器，没有的话用默认用户实现了Comparable接口，对传入的类强转为Comparable,如果都没有，自然会被编译错误，抛出异常。

• 所以，综上所述。BinarySearchTree的compare应该这样写：

  	/**
       * 返回的值>0:e1>e2
       * 返回的值<0:e1<e2
       * 返回的值=0:e1=e2
       * @param e1
       * @param e2
       * @return
       */
      public int compare(E e1, E e2){
          //二叉搜索树一定是可以根据对象来进行比较的
          //如果对象有自己的比较器，则只需传入两个参数即可
          if (comparator != null){
             return comparator.compare(e1,e2);
          }
          //如果没有自己的比较器
          return ((Comparable<E>)e1).compareTo(e2);
      }
  
      public void remove(E element) {
  
      }
  

• add方法

  • 完成了以上这些添加节点的方法，其实就很好写了，无非就是比我小的往左拐，比我大的往右拐，相等的不操作。（大于0往右拐，小于0往左拐，相等不操作）

  /**
       * 添加节点
       * @param element
       */
  
      public void add(E element) {
          elementNotNullCheck(element);   //校验element是否不为null
          //添加第一个节点
          if (root == null){
              root = new Node(element,null);
              size++;
              return;
          }
          //添加的不是第一个节点
          //1.先找到父节点parent,以及记录插入节点的方向
          Node<E> node = root;
          Node<E> parent = root;//记录父节点
          int res = 0;//记录方向
          while(node != null){
              parent = node;
              res = compare(element , node.element);
              //res>0 说明在节点的右边
              if (res > 0){
                  node = node.right;
              }
              //res <0 说明在节点的左边
              else if(res < 0){
                  node = node.left;
              }else{//相等
                  return;
              }
  
          }
          //2.通过节点方向,插入新节点
          Node<E> newnode = new Node<>(element,parent);
          if ( res > 0 ){
              parent.right = newnode;
          }else{
              parent.left = newnode;
          }
          size++;
      }
  

测试添加方法是否正确

• 测试代码：

  public class BinarySearchTreeTest {
      static int [] arr = new int[]{7,4,9,2,5,8,11,3};
      public static void main(String[] args) {
          BinarySearchTree<Integer> bst = new BinarySearchTree<>();
          for (int i = 0 ; i < arr.length ; i++){
              bst.add(arr[i]);
          }
          BinaryTrees.println(bst);
      }
  }
  

• 测试结果

PS:需要代码的请留下邮箱，bingo···