我的中国大学MOOC-陈越、何钦铭-数据结构-2018秋代码仓:https://github.com/617076674/MOOC-DataStructure-2018-Autumn
题目描述:
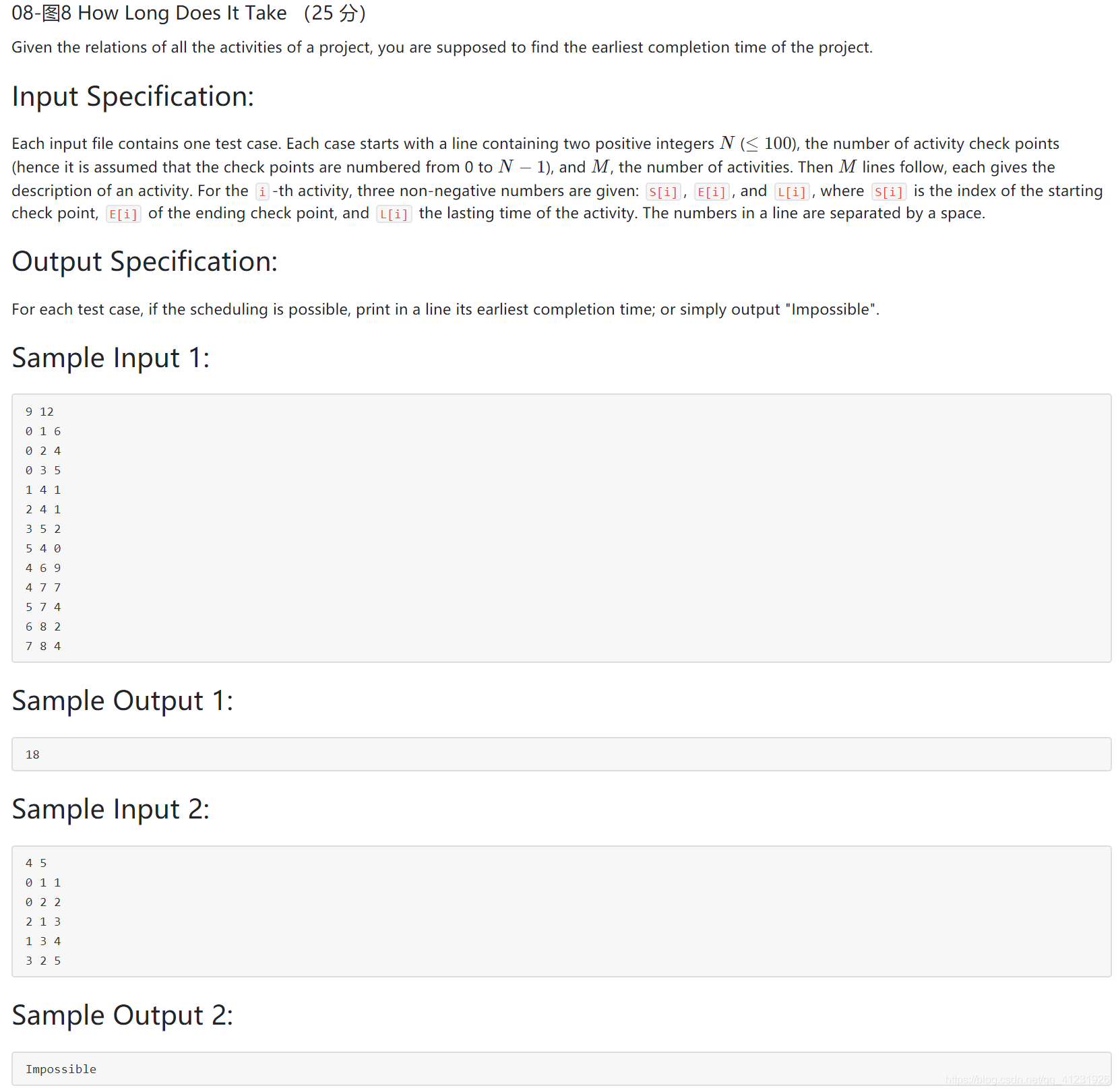
知识点:关键路径
思路:对边取相反数,用SPFA算法求最短路径
为了找到起点,我们还需要统计每一个点的入度,其中入度为0的点才可能是起点。对所有入度为0的点,我们都以其为起点做SPFA算法,取其到其他点的最小距离,如果该最小距离比当前记录的最小距离还要小,就更新当前记录的最小距离。
一次SPFA算法的时间复杂度是O(kM)。空间复杂度是O(N ^ 2)。
C++代码:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct node{
int v;
int len;
node(int _v, int _len){
v = _v;
len = _len;
}
};
int N, M, inDegree[100], INF = 1000000000, minLen = INF;
vector<node> graph[100];
int countInq[100], d[100];
bool inq[100];
void init();
bool spfa(int s);
int main(){
scanf("%d %d", &N, &M);
fill(inDegree, inDegree + N, 0);
int S, E, L;
for(int i = 0; i < M; i++){
scanf("%d %d %d", &S, &E, &L);
graph[S].push_back(node(E, -L));
inDegree[E]++;
}
for(int i = 0; i < N; i++){
if(inDegree[i] == 0){
init();
bool flag = spfa(i);
if(flag){
for(int j = 0; j < N; j++){
if(d[j] < minLen){
minLen = d[j];
}
}
}
}
}
if(minLen == INF){
printf("Impossible\n");
}else{
printf("%d\n", -minLen);
}
return 0;
}
void init(){
fill(countInq, countInq + N, 0);
fill(d, d + N, INF);
fill(inq, inq + N, false);
}
bool spfa(int s){
queue<int> q;
q.push(s);
d[s] = 0;
countInq[s]++;
inq[s] = true;
while(!q.empty()){
int u = q.front();
q.pop();
inq[u] = false;
for(int i = 0; i < graph[u].size(); i++){
int v = graph[u][i].v;
int len = graph[u][i].len;
if(len + d[u] < d[v]){
d[v] = len + d[u];
if(!inq[v]){
q.push(v);
inq[v] = true;
countInq[v]++;
if(countInq[v] > N - 1){
return false;
}
}
}
}
}
return true;
}C++解题报告:
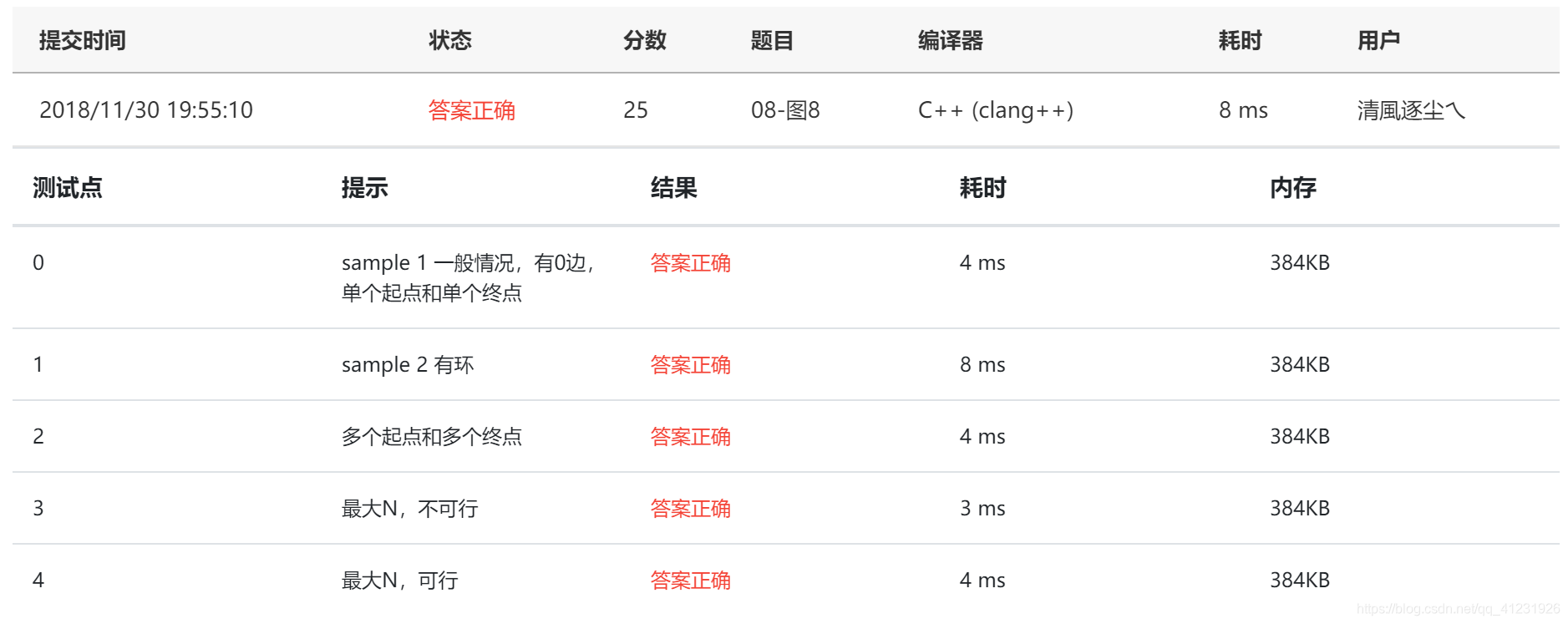








 本文探讨了在数据结构课程中关键路径的概念及其求解方法,通过SPFA算法寻找图中从起点到各点的最短路径,特别适用于处理带有负权边的问题。介绍了算法的实现细节,包括节点结构定义、初始化过程、SPFA算法流程及时间复杂度分析。
本文探讨了在数据结构课程中关键路径的概念及其求解方法,通过SPFA算法寻找图中从起点到各点的最短路径,特别适用于处理带有负权边的问题。介绍了算法的实现细节,包括节点结构定义、初始化过程、SPFA算法流程及时间复杂度分析。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








