PAT-ADVANCED1019——General Palindromic Number

最新推荐文章于 2022-07-13 12:09:40 发布

清風逐尘乀

最新推荐文章于 2022-07-13 12:09:40 发布

阅读量323

点赞数

CC 4.0 BY-SA版权

分类专栏： PAT甲级真题题解文章标签： PAT 甲级进制转换 1019 General Palindromic Number

本文链接：https://blog.youkuaiyun.com/qq_41231926/article/details/83955170

PAT甲级真题题解专栏收录该内容

155 篇文章

订阅专栏

本文深入解析PAT-ADVANCED中广义回文数问题，介绍如何判断一个十进制数在不同进制下是否为回文数。通过C++代码实现进制转换及回文判断，分享解题思路与技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我的PAT-ADVANCED代码仓：https://github.com/617076674/PAT-ADVANCED

原题链接：https://pintia.cn/problem-sets/994805342720868352/problems/994805487143337984

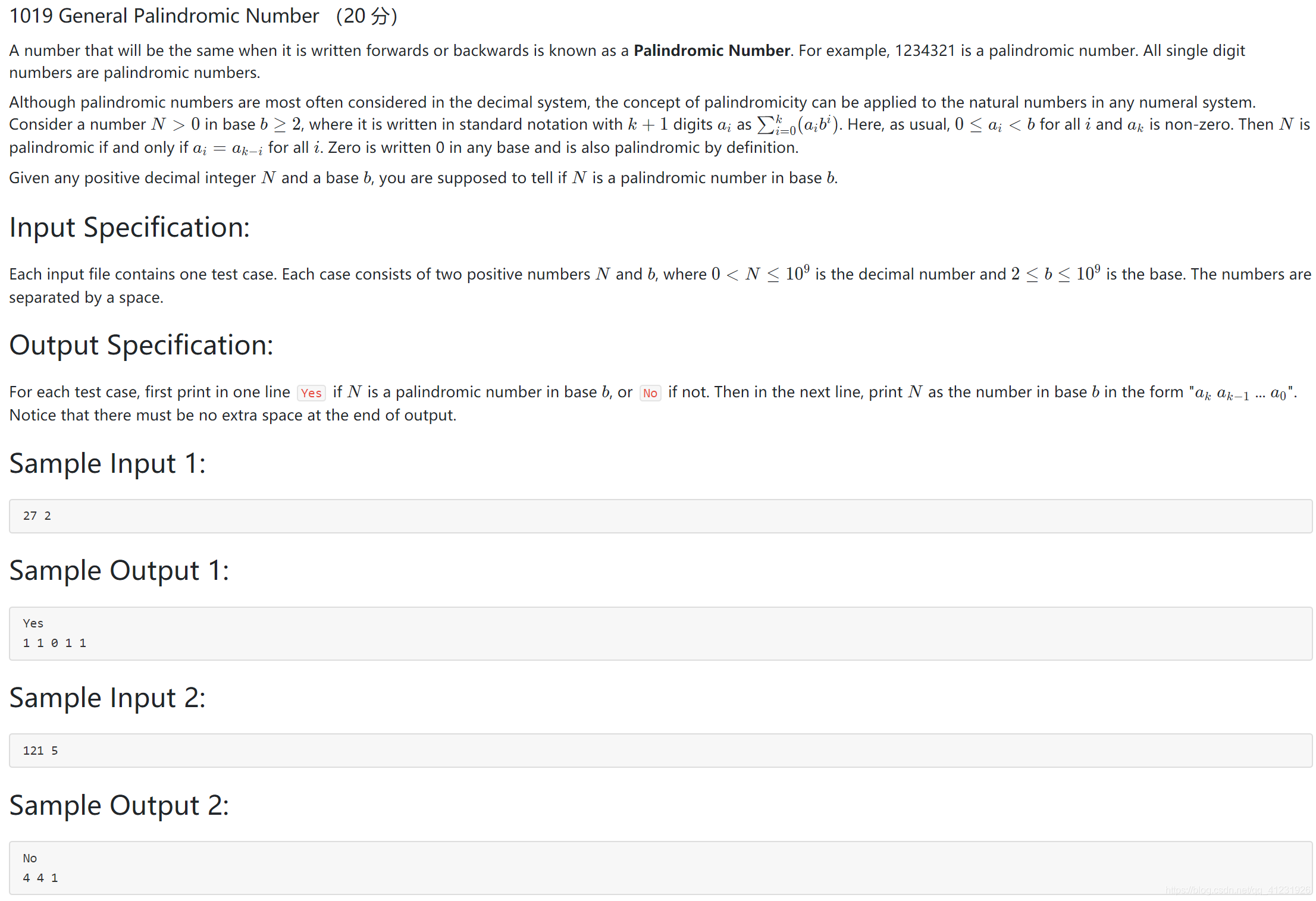
题目描述：

题目翻译：

1019 广义回文数

向前或向后书写时相同的数字称为回文数字。例如，1234321是回文数字。所有单个数字都是回文数字。

虽然回文数通常在十进制中被考虑，但回文概念可以应用于任何数字系统中的自然数。考虑基数b >= 2中的数字N > 0，该数字k + 1个数字ai可以转换为10进制数(a0 * b ^ 0 + a1 * b ^ 1 + ... + ak * b ^k)。通常，0 <= ai < b(i = 1, 2, ..., k)且ak非零。当且仅当ai = ak - i(i = 1, 2, ..., k)时，N是一个回文数。Zero在任何进制中都写为0，并且根据定义也是回文。

给定任何正十进制整数N和进制b，你需要判断N是否是b进制下的回文数。

输入格式：

每个输入文件包含一个测试用例。每个测试用例由两个正数N和b组成，其中0 < N <= 10代表十进制数，2 <= b <= 10代表进制。数字用空格分隔。

输出格式：

对每个测试用例，如果N是基数b中的回文数，在一行中打印“Yes”，否则打印“No”。然后在下一行中，以“akak - 1...a0”的形式打印N转换为b进制数字的形式。请注意，输出结束时不得有额外的空格。

输入样例1：

27 2

输出样例1：

Yes
1 1 0 1 1

输入样例2：

121 5

输出样例2：

No
4 4 1

知识点：进制转换

思路：先进制转换，再判断是否是回文数

时间复杂度和空间复杂度均是O(n)，其中n为进制转换后的位数。

C++代码：

#include<iostream>
#include<vector>

using namespace std;

bool isPalindromic(vector<int> result);

int main(){
	int N, b;
	scanf("%d %d", &N, &b);
	vector<int> result;
	while(N > 0){
		result.push_back(N % b);
		N /= b;
	}
	if(isPalindromic(result)){
		printf("Yes\n");
	}else{
		printf("No\n");
	}
	for(int i = result.size() - 1; i >= 0; i--){
		printf("%d", result[i]);
		if(i != 0){
			printf(" ");
		}else{
			printf("\n");
		}
	}
	return 0;
}

bool isPalindromic(vector<int> result){
	for(int i = 0; i < result.size() / 2; i++){
		if(result[i] != result[result.size() - 1 - i]){
			return false;
		}
	}
	return true;
}

C++解题报告：