我的PAT-ADVANCED代码仓:https://github.com/617076674/PAT-ADVANCED
原题链接:https://pintia.cn/problem-sets/994805342720868352/problems/994805365537882112
题目描述:
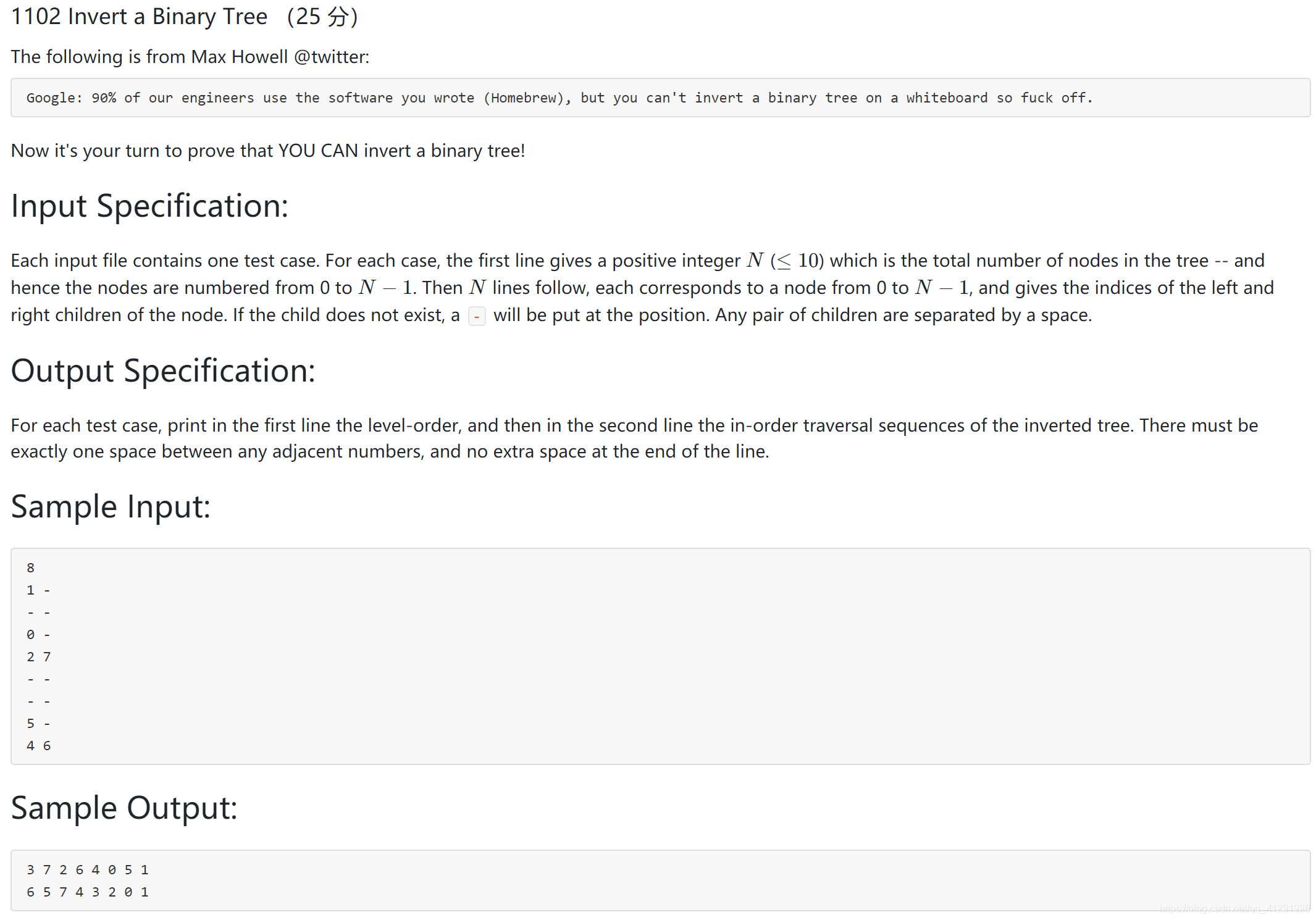
题目翻译:
1102 翻转一棵二叉树
下面这段话摘自Max Howell的推特:
Google:我们90%的工程师都使用您编写的软件(Homebrew),但您无法在白板上反转二叉树,所以滚蛋。现在轮到你来证明你可以翻转一棵二叉树。
输入格式:
每个输入文件包含一个测试用例。在每个测试用例中,第一行给出了一个正整数N(<= 10),代表树中的节点总数——节点编号从0 ~ N - 1。接下来的N行,每行依次对应0 ~ N - 1的一个节点,给出其左右子节点的索引。如果其左孩子或右孩子不存在,则用“-”代替。每对孩子节点用一个空格分隔。
输出格式:
对每个测试用例,在第一行输出翻转后的二叉树的层序遍历,在第二行输出其中序遍历。相邻数字间必须以一个空格分隔,行末不得有多余空格。
输入样例:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6输出样例:
3 7 2 6 4 0 5 1
6 5 7 4 3 2 0 1知识点:递归、二叉树的层序遍历、中序遍历
思路:递归地翻转一棵二叉树
翻转过程的伪代码如下:
递归终止条件:如果是一棵空树,直接返回输入的空节点即可。
递归过程:如果不是一棵空树,分别翻转左右子树,再交换左右子树即可。注意翻转过程中需要有中间变量来分别记录左右子树翻转后的的结果。
翻转过程时间复杂度和空间复杂度均是O(h),其中h为树的高度。
中序遍历的时间复杂度是O(N)。空间复杂度是O(h)。
层序遍历的时间复杂度和空间复杂度均是O(N)。
C++代码:
#include<iostream>
#include<string>
#include<vector>
#include<queue>
using namespace std;
struct node {
int lchild;
int rchild;
};
int N;
node Node[10];
bool flag[10] = {false};
vector<int> levelOrder;
vector<int> inOrder;
int inverseTree(int root);
void levelOrderTraversal(int root);
void inOrderTraversal(int root);
int main() {
cin >> N;
string lchild, rchild;
for(int i = 0; i < N; i++) {
cin >> lchild >> rchild;
if(lchild.compare("-") == 0) {
Node[i].lchild = -1;
} else {
int num = lchild[0] - '0';
Node[i].lchild = num;
flag[num] = true;
}
if(rchild.compare("-") == 0) {
Node[i].rchild = -1;
} else {
int num = rchild[0] - '0';
Node[i].rchild = num;
flag[num] = true;
}
}
int root = -1;
for(int i = 0; i < N; i++) {
if(!flag[i]) {
root = i;
break;
}
}
root = inverseTree(root);
levelOrderTraversal(root);
inOrderTraversal(root);
for(int i = 0; i < levelOrder.size(); i++) {
cout << levelOrder[i];
if(i != levelOrder.size() - 1) {
cout << " ";
}
}
cout << endl;
for(int i = 0; i < inOrder.size(); i++) {
cout << inOrder[i];
if(i != inOrder.size() - 1) {
cout << " ";
}
}
cout << endl;
return 0;
}
int inverseTree(int root) {
if(root == -1) {
return root;
}
int rootLeft = inverseTree(Node[root].rchild);
int rootRight = inverseTree(Node[root].lchild);
Node[root].lchild = rootLeft;
Node[root].rchild = rootRight;
return root;
}
void levelOrderTraversal(int root) {
queue<int> q;
q.push(root);
while(!q.empty()) {
int now = q.front();
levelOrder.push_back(now);
q.pop();
if(Node[now].lchild != -1) {
q.push(Node[now].lchild);
}
if(Node[now].rchild != -1) {
q.push(Node[now].rchild);
}
}
}
void inOrderTraversal(int root) {
if(root == -1) {
return;
}
inOrderTraversal(Node[root].lchild);
inOrder.push_back(root);
inOrderTraversal(Node[root].rchild);
}C++解题报告:
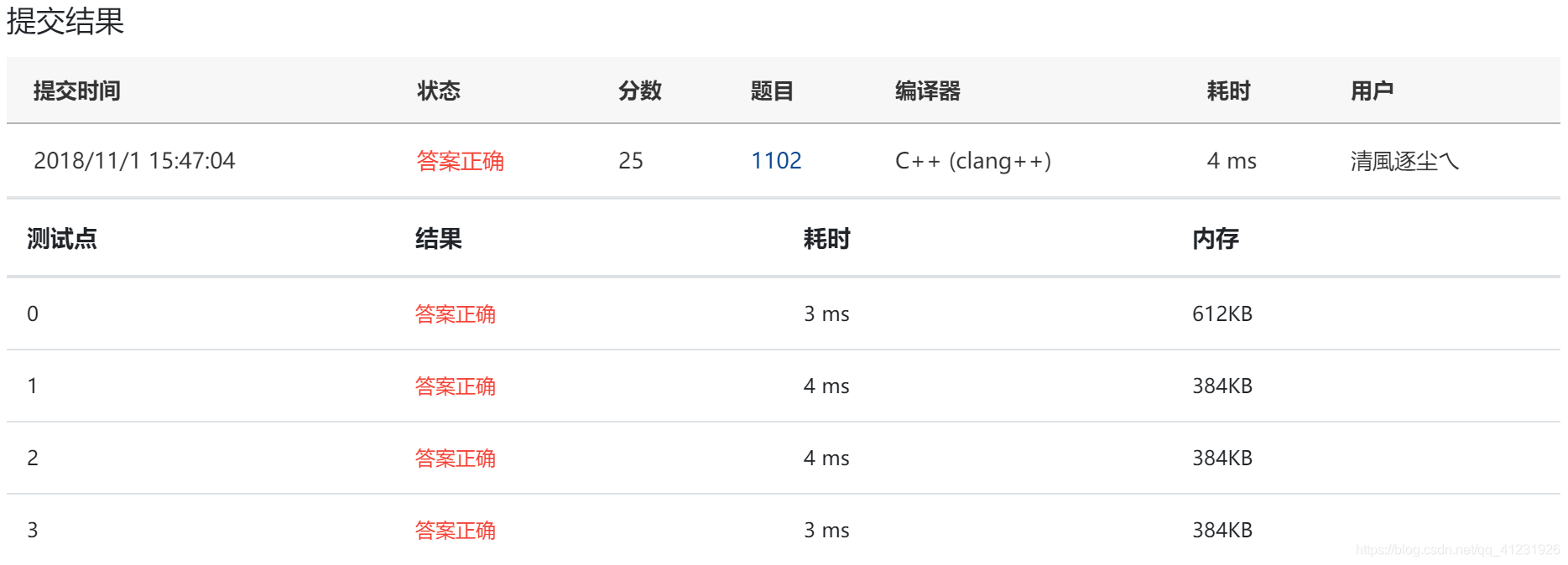








 本文介绍了一种翻转二叉树的方法,并通过递归实现。同时,讲解了层序遍历和中序遍历的算法,提供了一个完整的C++代码示例,帮助读者理解和实践二叉树的操作。
本文介绍了一种翻转二叉树的方法,并通过递归实现。同时,讲解了层序遍历和中序遍历的算法,提供了一个完整的C++代码示例,帮助读者理解和实践二叉树的操作。
















 869
869

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








