我的LeetCode代码仓:https://github.com/617076674/LeetCode
原题链接:https://leetcode-cn.com/problems/combination-sum/description/
题目描述:
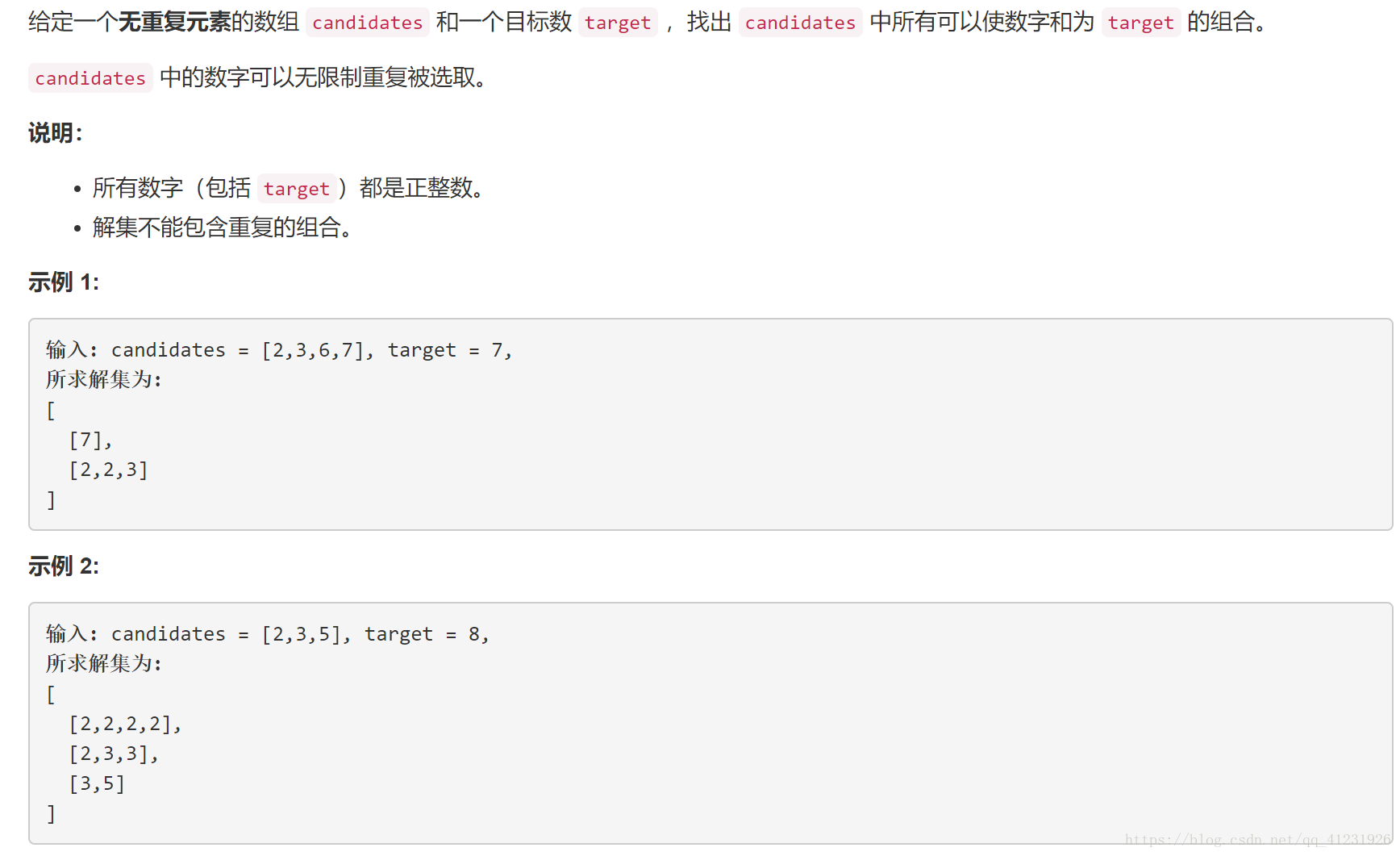
知识点:回溯、递归
思路:用回溯法寻找所有可能的组合
本题要求的是candidates数组中所有可以使数字和为target的组合,我们需要穷尽所有的candidates数组可能产生的组合,因此很明显的,我们需要用回溯算法来解决问题。在解决问题的过程中有以下几个注意点:
(1)在Solution类中新建一个List<List<Integer>>类型的私有成员变量listList用以保存结果,可以防止在递归函数中重复传递该值。
(2)本题要求的是组合,并不是排列,我们假设每一次加入到我们list中的元素都大于等于list中最后一个元素,这样可以防止出现重复的组合。因此,我们在递归之前要先对candidates数组进行排序。
(3)我们的递归函数private void combinationSum(int[] candidates, int target, List<Integer> list, int sum)的定义如下:
在candidates数组中寻找和为target的组合,目前我们list中存放的数据和为sum,我们将要在candidates中寻找下一个存入list的数字。
递归终止条件:
当sum的值大于等于target的值时,由于题目限定了所有数字都是正整数,如果我们再向list中添加元素,sum必将越来越大,不可能等于target,我们直接返回。但在返回之前我们需要判断sum是否与target相等,如果相等,我们保存list集合进listList中。
注意这里不能使用listList.add(list),而应该使用listList.add(new ArrayList<>(list))。因为list是一个引用,在回溯过程中,其指向的集合是在不断改变的,我们要记录的是递归到底时list中存储的数据,因此我们需要根据list来新建一个ArrayList来保存。
递归过程:
如果list中没有任何元素,其新增的下一个元素可以是candidates中的任意一个元素。注意list集合的手动回溯过程。
如果list中有元素,其新增的下一个元素必须等于等于list中最后一个元素。注意list集合的手动回溯过程。
关于时间复杂度,一开始我们对candidates数组进行了排序,该过程的时间复杂度是O(nlogn),其中n为candidates数组的长度。而整个递归过程的时间复杂度,如果考虑最坏情况,即target为candidates中所有元素之和,其时间复杂度是O(n ^ n)。因此总的时间复杂度应该是O(n ^ n)。而空间复杂度就是递归深度,最坏情况应该是递归target次,因此空间复杂度为O(target)级别。
JAVA代码:
public class Solution {
private List<List<Integer>> listList;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
listList = new ArrayList<>();
Arrays.sort(candidates);
combinationSum(candidates, target, new ArrayList<>(), 0);
return listList;
}
private void combinationSum(int[] candidates, int target, List<Integer> list, int sum) {
if(sum >= target) {
if(sum == target) {
listList.add(new ArrayList<>(list));
}
return;
}
if(list.size() == 0) {
for (int i = 0; i < candidates.length; i++) {
list.add(candidates[i]);
combinationSum(candidates, target, list, sum + candidates[i]);
list.remove(list.size() - 1);
}
}else {
for (int i = 0; i < candidates.length; i++) {
if(candidates[i] >= list.get(list.size() - 1)) {
list.add(candidates[i]);
combinationSum(candidates, target, list, sum + candidates[i]);
list.remove(list.size() - 1);
}
}
}
}
}
LeetCode解题报告:
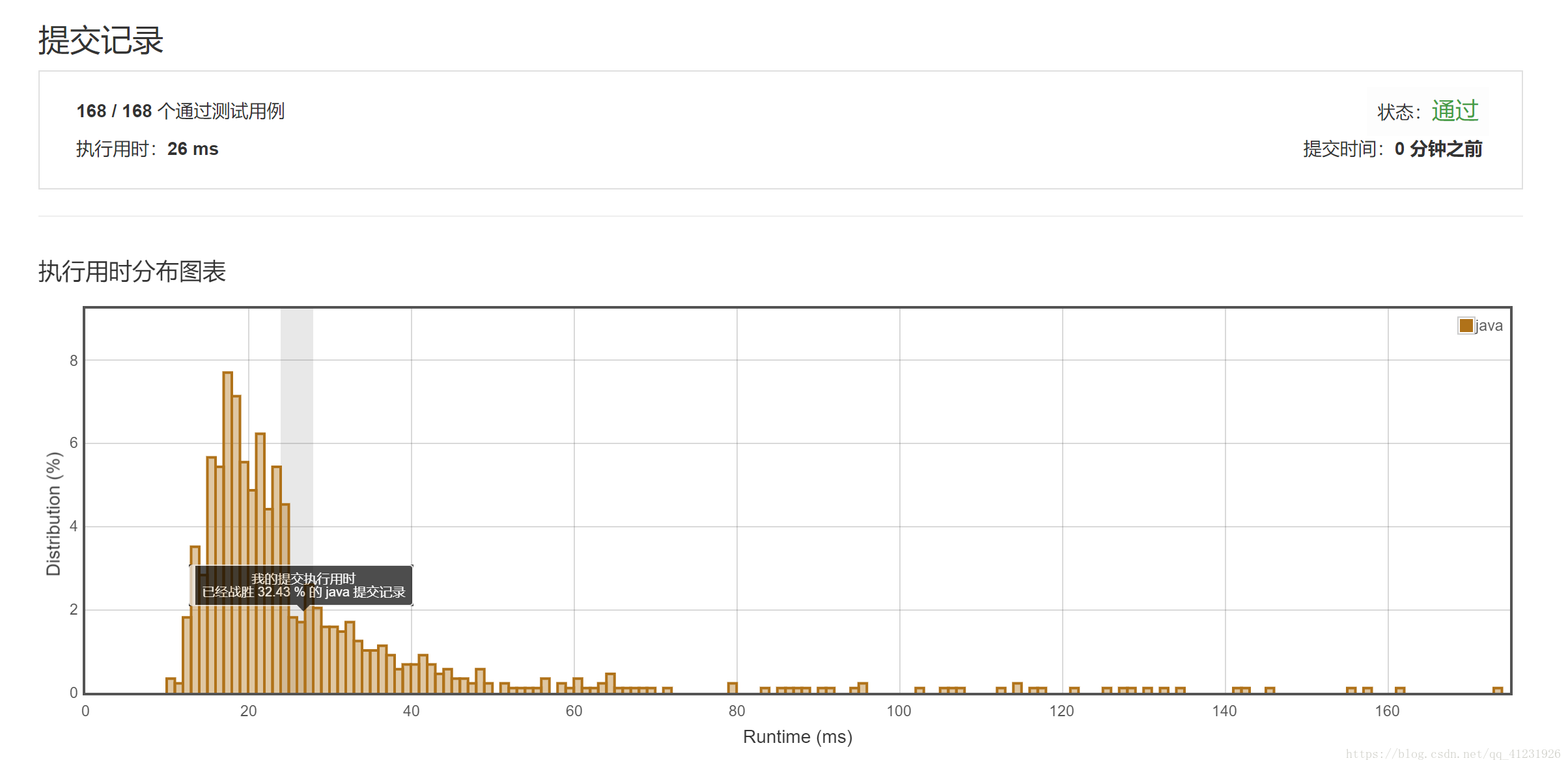





 本文介绍LeetCode上一道经典题目“组合求和”的解题思路与Java代码实现。采用回溯法解决如何从数组中找出所有可能的组合使数字和为目标值。通过排序和递归函数避免重复组合。
本文介绍LeetCode上一道经典题目“组合求和”的解题思路与Java代码实现。采用回溯法解决如何从数组中找出所有可能的组合使数字和为目标值。通过排序和递归函数避免重复组合。
















 181
181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








