2021-05-12：二叉树，二叉搜索树，98，235，236

主要内容：

Tree, Binary Tree, Binary Search Tree

Graph

 

Tree:

 

 

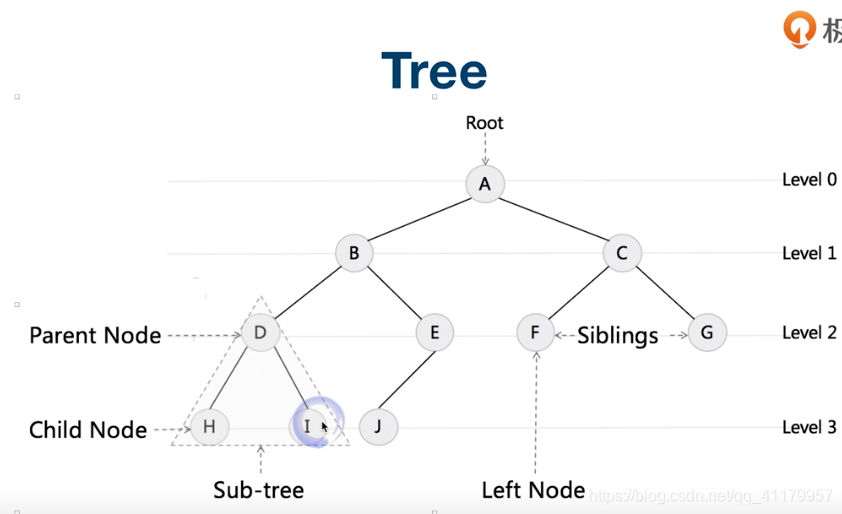
Linked List 就是特殊化的 Tree

Tree 就是特殊化的 Graph

二叉搜索树：

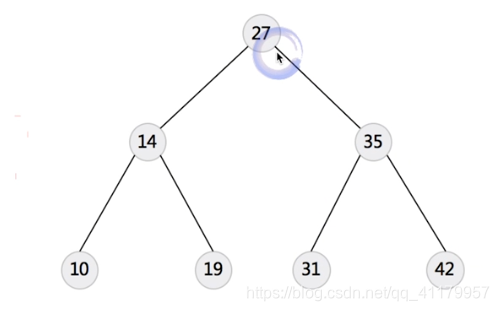
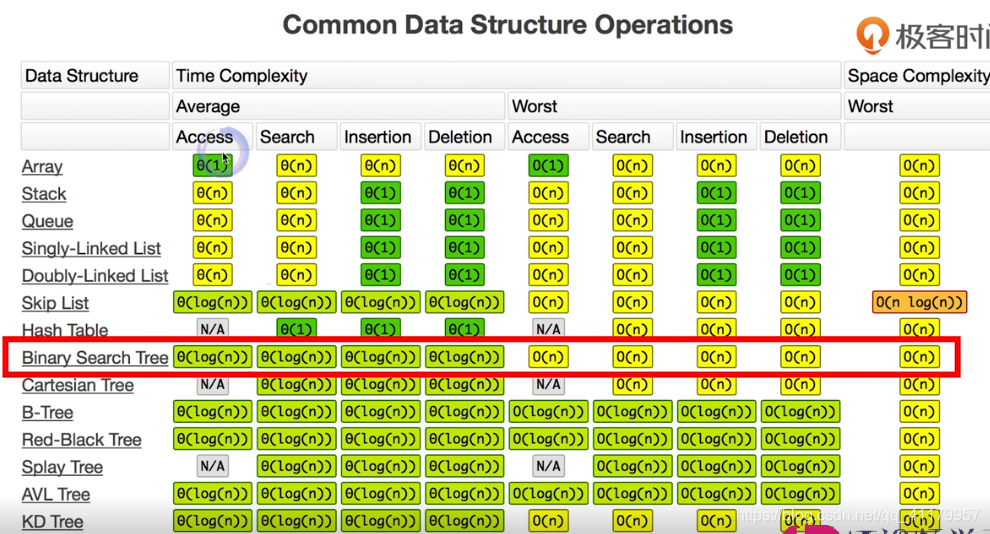
二叉树的遍历：  这里看的是根的位置

Pre-order 前序：根左右

In-order  中序： 左根右

Post-order 后序：左右根

用递归解答顺序

一般遍历是：深度优先，广度优先，以及搜索

方法一，先用inorder方式打出来，然后进行对比

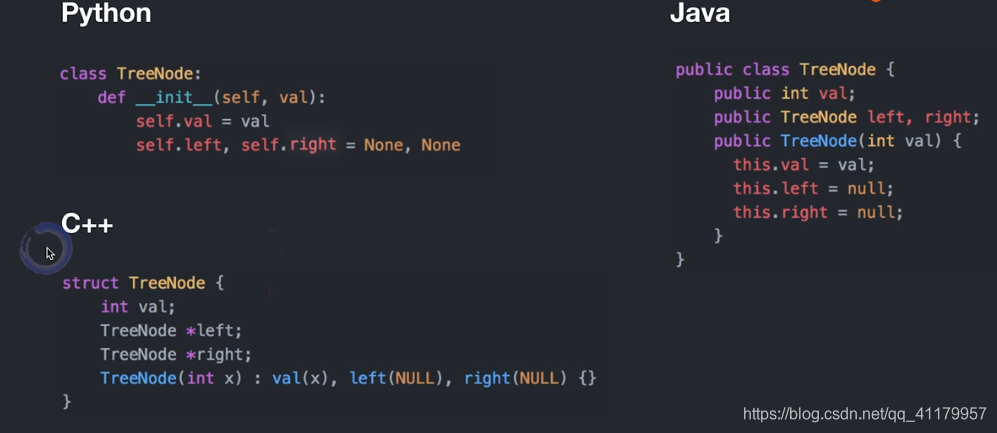
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        inorderlist = self.inorder(root)
        return inorderlist == list(sorted(set(inorderlist)))
    def inorder(self, root:TreeNode):
        if root is None:
            return []
        return self.inorder(root.left) + [root.val] +self.inorder(root.right)

这里用sorted set的原因是，避免

这样的情况。不是树的情况

python 用 +可以拼接list

 

 

方法二：先判断这个点是否为中值点。

然后遍历左子树。

然后遍历右子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        return self.roothelper(root,-2**32,2**32)

    def roothelper(self, root1: TreeNode, min_v:int, max_v:int)-> bool:
        if root1 == None:
            return True
        if root1.val<max_v and root1.val > min_v:
            pass
        else:
            return False
        if ( self.roothelper(root1.left,min_v,root1.val))== False:
            return False
        if (self.roothelper(root1.right,root1.val,max_v)) ==False:
            return False
        return True

 

用 ==False, 比 not 会减少运行时间

 

 

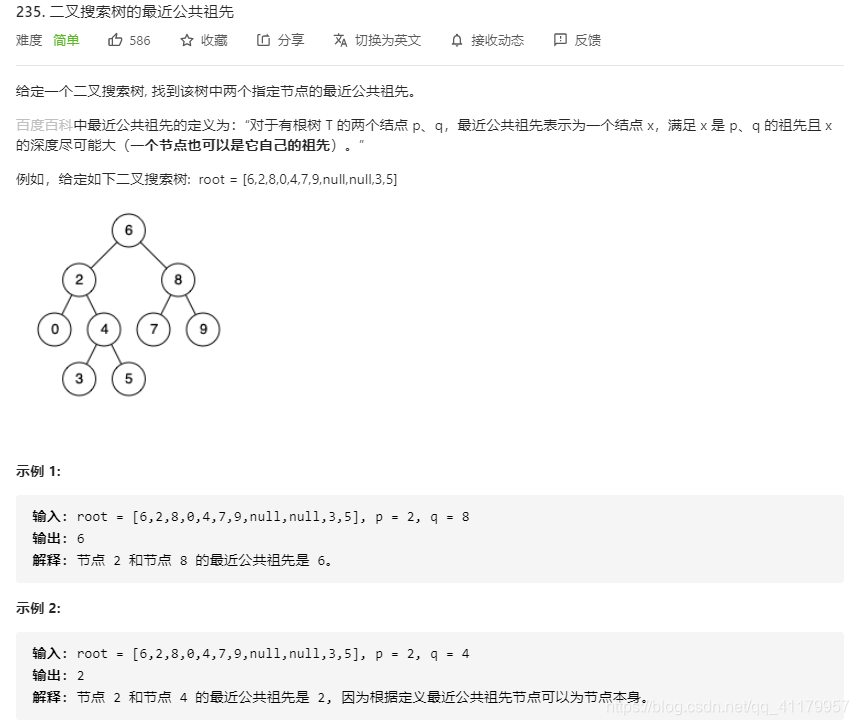
235:

 

执行用时：100 ms, 在所有 Python3 提交中击败了27.95%的用户

内存消耗：18.7 MB, 在所有 Python3 提交中击败了87.82%的用户

 

解法1： 因为是二叉搜索树，左子树小于中节点，右子树大于中节点

，所以如果pq都小于此节点的值，则向右子树遍历，

如果都大于，向左子树遍历，

如果不是，则是介于其中，就是此节点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if p.val < root.val and q.val <root.val :
            return self.lowestCommonAncestor(root.left, p, q)
        elif p.val > root.val and q.val >root.val:
            return self.lowestCommonAncestor(root.right,p,q)
        else:
            return root    
    

解法2： copy大佬的思路：

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while (root.val - p.val) * (root.val - q.val) > 0: 
            root = (root.left, root.right)[p.val > root.val]
        return root
            

 

如果root在区间中间，则返回root。

如果不在，说明pq同号。如果p大， 则后面条件满足，为True:[1]， 索引元组[1]的位置，root = root.right

反之则为[0]， root = root. left

 

此题思路重点！！抓住在二叉搜索树中公共节点一定是在pq中间。因为左子树小，右子树大的原则

 

 

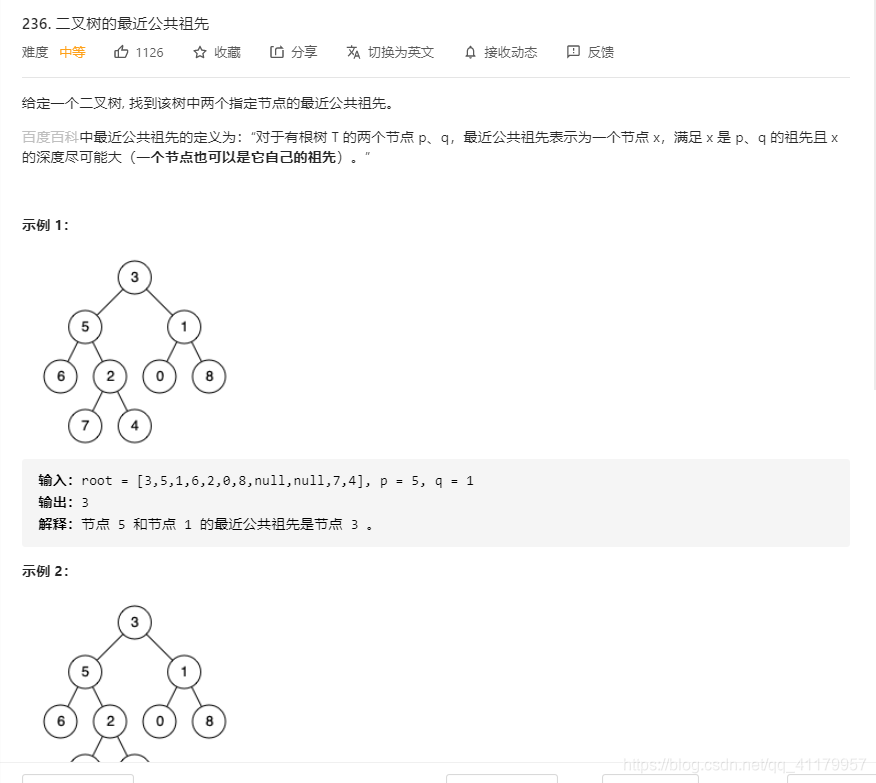
此题思路：

以root为中节点，左右子树去找p和q

在同一回溯级里：

left就是去root的左子树找此节点

right就是去root的右子树找此节点

如果左边没有， 则说明两个都在右边或者  一个为null一个在右边： 此时返回right，要么返回的是存在的那个节点，要么返回的是右边存在的共同父节点

如果右边没有，则同理

如果两边都没有，则返回空

如果两边都有，则返回root,说明p q存在于此root的两边，则root为他们的共同父节点

 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root:
            return None
        if root == p or root ==q :
            return root
        right = self.lowestCommonAncestor( root.right, p, q)
        left = self.lowestCommonAncestor( root.left, p,q)
        if not right and not left:
            return
        elif not right and left:
            return left
        elif not left and right:
            return right
        else:
            return root