为什么学习线性代数_工程应用简介

---

前言：
对于理工科学生来说，线性代数是必不可少的一门课，其在通信、AI、计算机、物理、机械工程等各个领域均有重要且广泛的应用。我们大学时所用的课本、老师讲的课，基本都注重怎么去计算，很少有提及应用场景、计算的原理以及几何上的解释，这就导致很多同学对这门课失去了兴趣，没了兴趣硬着头皮学，只会感到“人生艰难”。
笔者以前也是搞不懂为什么要学线性代数，算出这个行列式有什么意义？把向量施密特正交化了有什么用？把这个矩阵对角化有什么用，等等一系列问题我好久都没弄懂，可惜大一时候比较贪玩，这些问题不了了之，等考研复习的时候，由于任务比较繁重，也只是学会计算和证明方法，关于这门课对科技的重要影响也没怎么去了解。直到读研后，上了矩阵论这门课(线性代数只是矩阵论的冰山一角…)，以及亲手做过一些项目，才深刻理解这门课的应用价值。
作为过来人，奉劝各位好好学这门课，尤其是有考研意向的同学，线性代数在考研数学中是必考的，不管数几，而且是最容易拿分的。对于理工科读研的同学，科研中躲不开线代。学线代时，一定要数形结合，几何的解释有助于理解。对于一些不理解的知识，可以在网上查一查，不要局限于百度，知乎、博客等均有许多大佬解释的很生动，实在查不到的欢迎与我讨论。

---

举个应用例子：

线性代数中，最基础的莫过于向量。这是一个抽象的概念，其实整个线性代数就是一门对事物进行抽象的学科，对于下面这个向量：

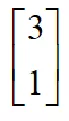
我们可将它看作是二维平面的一个箭头，起点在(0,0)，终点在(3,1)，矩阵论中有一种线性变换叫做旋转变换，它不改变向量的模值大小，只改变方向，假设我们要使上面这个箭头沿逆时针旋转θ角度，那么可以构建一个旋