简介
利用c++计算文法的firsr,follow,select 集合,然后判断文法是否为LL1文法,并构造预测分析表,对输入字符串进行分析
参考代码
#include <iostream>
#include <map>
#include <vector>
#include <set>
#include <list>
#include <cstdio>
#include <iomanip>
using namespace std;
typedef char grammarType;
grammarType start, S; //开始符号,S用来作为输入
map<grammarType, int> ter; //终结符集合
vector<grammarType> terInx; //通过索引查找终结符
map<grammarType, int> nonter; //非终结符集合
vector<grammarType> nontInx; //通过索引查找非终结符
vector<grammarType> language; //需要进行分析的语言,即输入字符串
int terNum, nontNum, proSize, Lsize; //终结符数目,非终结符数目,产生式数目,语言的长度
struct Production
{
int leftPart; //左部非终结符的索引
vector<int> rightPart; // 右边产生式索引
vector<bool> flag; //标记右边相关产生式是终结符(false),非终结符(false)
};
vector<Production> pro; //产生式
vector<int> *nontPro; // 各个非终结符的产生式的集合
vector<bool> proEmpty; //记录各个产生式能否推出空 true能,false不能
set<int> *First; //各个非终结符的First集合
#define FirstIt(x) for (itSet = First[(x)].begin(); itSet != First[(x)].end(); ++itSet)
set<int> *Follow; // 各个非终结符的Follow集合
#define FollowIt(x) for (itSet = Follow[(x)].begin(); itSet != Follow[(x)].end(); ++itSet)
set<int> *Select; //各个产生式的Select的集合
#define SelectIt(x) for (itSet = Select[(x)].begin(); itSet != Select[(x)].end(); ++itSet)
set<int>::iterator itSet; // set迭代集合
struct edge
{
int v, s; //u->v一条边 s代表状态,1 终结符,
edge(int v, int s) : v(v), s(s) {}
}; //利用关系图法求解First
vector<int> *graph; //图
int *inDe; //计算入度
vector<int> top; //定义出栈顺序,即计算顺序
vector<int> nontEmpty; //能否推出空,0未定,1代表是,2代表否
vector<int> *analyzeTable; //构造LL1文法的预测分析表
struct Sign
{
int Inx;
bool flag; //符合索引 表示文法分析栈中的字符是否为非终结符 true 非终结符
Sign(int a, bool b) : Inx(a), flag(b) {}
Sign() {}
};
vector<Sign> analysisStack; //用数组模拟LL1文法分析栈
#define out(width, str) cout << setw((width)) << setiosflags(ios::left) << ((str))
void getEmpty(); //求非终结符能否推出空集
void geFirst(); //计算文法First集合
void getFollow(); //计算文法Follow集合
void getSelect(); //计算产生式的Select集合
bool judegLL1(); //判断是否为LL1文法
void getAnalyzeTable(); //得到LL1文法的预测分析表
void analysis(); //对所得语言进行分析
int main()
{
cout << "请输入文法开始符合:";
cin >> start;
cout << "请输入非终结符的数目:";
cin >> nontNum;
First = new set<int>[nontNum];
Follow = new set<int>[nontNum];
nontPro = new vector<int>[nontNum];
cout << "请依次输入非终结符:";
for (int i = 0; i < nontNum; ++i)
{
cin >> S;
nonter[S] = i;
nontInx.push_back(S);
}
cout << "请输入终结符的数目:";
cin >> terNum;
cout << "请依次输入终结符:(用二个符合表示空和结束符并放在末尾)";
for (int i = 0; i < terNum; ++i)
{
cin >> S;
ter[S] = i;
terInx.push_back(S);
}
cout << "请依次输入产生式的数目:";
cin >> proSize;
Select = new set<int>[proSize];
proEmpty.insert(proEmpty.begin(), proSize, false);
cout << "请依次输入产生式:";
int t;
Production p;
for (int i = 0; i < proSize; ++i)
{
cin >> S >> t;
p.leftPart = nonter[S];
nontPro[p.leftPart].push_back(i);
for (int j = 0; j < t; ++j)
{
cin >> S;
if (nonter.find(S) != nonter.end())
{
p.rightPart.push_back(nonter[S]);
p.flag.push_back(true);
}
else
{
p.rightPart.push_back(ter[S]);
p.flag.push_back(false);
}
}
pro.push_back(p);
p.rightPart.clear();
p.flag.clear();
}
getEmpty();
geFirst();
getFollow();
getSelect();
if (judegLL1() == false)
return 0;
getAnalyzeTable();
cout << "请输入要分析的语言的长度: ";
cin >> Lsize;
cout << "请输入要分析的语言(带输入结束符):";
for (int i = 0; i < Lsize; ++i)
{
cin >> S;
language.push_back(S);
}
analysis();
}
void getEmpty()
{
nontEmpty.clear();
nontEmpty.insert(nontEmpty.begin(), nontNum, 0); //初始化
vector<int> nonProNum(nontNum, 0);
list<int> wait;
int nul = terNum - 2, j, i, ltmp;
for (int i = 0; i < proSize; ++i)
{
for (j = 0, ltmp = pro[i].leftPart; j < pro[i].flag.size(); ++j)
{
if (pro[i].flag[j] == false && pro[i].rightPart[j] == nul)
nontEmpty[ltmp] = 1;
if (pro[i].flag[j] == false)
break;
}
if (j == pro[i].flag.size())
{
wait.push_front(i);
nonProNum[ltmp]++;
}
}
for (int i = 0; i < nontNum; ++i)
{
if (nontEmpty[i] == 0 && nonProNum[i] == 0)
nontEmpty[i] = 2;
}
list<int>::iterator itlist = wait.begin();
while (itlist != wait.end())
{
ltmp = pro[*itlist].leftPart;
if (nontEmpty[ltmp])
itlist = wait.erase(itlist), nonProNum[ltmp]--;
else
++itlist;
}
itlist = wait.begin();
while (!wait.empty())
{
if (itlist == wait.end())
itlist = wait.begin();
ltmp = pro[*itlist].leftPart;
if (nontEmpty[ltmp])
{
itlist = wait.erase(itlist);
continue;
}
for (j = 0, i = *itlist; j < pro[i].flag.size(); ++j)
{
if (nontEmpty[pro[i].rightPart[j]] == 2)
{
itlist = wait.erase(itlist);
nonProNum[ltmp]--;
if (nonProNum[ltmp] == 0)
nontEmpty[ltmp] = 2;
break;
}
else if (nontEmpty[pro[i].rightPart[j]] == 0)
{
itlist++;
break;
}
}
if (j == pro[i].flag.size())
{
nontEmpty[ltmp] = 1;
itlist = wait.erase(itlist);
}
}
}
void topSort()
{
int *sta = new int[nontNum];
int p = 0, v, u;
top.clear();
for (int i = 0; i < nontNum; ++i)
if (inDe[i] == 0)
sta[p++] = i;
while (p)
{
v = sta[--p];
top.push_back(v);
for (int i = 0; i < graph[v].size(); ++i)
{
u = graph[v][i];
inDe[u]--;
if (!inDe[u])
sta[p++] = u;
}
}
}
void geFirst()
{
int i, j, ltmp, rtmp;
delete[] graph;
graph = new vector<int>[nontNum];
delete[] inDe;
inDe = new int[nontNum];
for (i = 0; i < nontNum; ++i)
inDe[i] = 0;
for (i = 0; i < proSize; ++i)
{
for (j = 0, ltmp = pro[i].leftPart; j < pro[i].flag.size(); ++j)
{
rtmp = pro[i].rightPart[j];
if (pro[i].flag[j])
{
graph[rtmp].push_back(ltmp);
inDe[ltmp]++;
if (nontEmpty[rtmp] == 2)
break;
}
else if (rtmp != terNum - 2)
{
First[ltmp].insert(rtmp);
break;
}
}
}
topSort();
for (i = 0; i < top.size(); ++i)
{
for (ltmp = top[i], itSet = First[ltmp].begin(); itSet != First[ltmp].end(); ++itSet)
{
for (j = 0; j < graph[ltmp].size(); ++j)
First[graph[ltmp][j]].insert(*itSet);
}
}
for (int i = 0; i < nontNum; ++i)
if (nontEmpty[i] == 1)
First[i].insert(terNum - 2);
cout << "各个非终结符的First集为: " << endl;
for (int i = 0; i < nontNum; ++i)
{
cout << "First( " << nontInx[i] << " ) = { ";
FirstIt(i) cout << terInx[*itSet] << " ";
cout << "}\n";
}
}
void getFollow()
{
int i, j, ltmp, rtmp, folFlag;
delete[] graph;
graph = new vector<int>[nontNum];
delete[] inDe;
inDe = new int[nontNum];
for (i = 0; i < nontNum; ++i)
inDe[i] = 0;
Follow[nonter[start]].insert(terNum - 1);
for (i = 0; i < proSize; ++i)
{
folFlag = true;
ltmp = pro[i].leftPart;
for (j = pro[i].flag.size() - 1; j > 0; --j)
{
rtmp = pro[i].rightPart[j];
if (pro[i].flag[j - 1])
{
if (pro[i].flag[j])
{
FirstIt(rtmp) if (*itSet != terNum - 2) Follow[pro[i].rightPart[j - 1]].insert(*itSet);
}
else
Follow[pro[i].rightPart[j - 1]].insert(rtmp), folFlag = false;
}
if (folFlag)
{
graph[ltmp].push_back(rtmp);
inDe[rtmp]++;
if (nontEmpty[rtmp] == 2)
folFlag = false;
}
}
if (pro[i].flag[0] && folFlag)
{
graph[ltmp].push_back(pro[i].rightPart[0]);
inDe[rtmp]++;
}
}
inDe[nonter[start]] = 0;
topSort();
for (i = 0; i < top.size(); ++i)
{
for (ltmp = top[i], itSet = Follow[ltmp].begin(); itSet != Follow[ltmp].end(); ++itSet)
{
for (j = 0; j < graph[ltmp].size(); ++j)
Follow[graph[ltmp][j]].insert(*itSet);
}
}
cout << "各个非终结符的Follow集为: " << endl;
for (i = 0; i < nontNum; ++i)
{
cout << "Follow( " << nontInx[i] << " ) = { ";
FollowIt(i) cout << terInx[*itSet] << " ";
cout << "}\n";
}
}
void getSelect()
{
int i, j, ltmp, rtmp;
for (i = 0; i < proSize; ++i)
{
for (j = 0, ltmp = pro[i].leftPart; j < pro[i].flag.size(); ++j)
{
if (pro[i].flag[j])
{
rtmp = pro[i].rightPart[j];
FirstIt(rtmp) Select[i].insert(*itSet);
if (nontEmpty[rtmp] == 2)
break;
}
else
{
Select[i].insert(pro[i].rightPart[j]);
break;
}
}
if (pro[i].flag[0] == false && pro[i].rightPart[0] == terNum - 2)
{
FollowIt(ltmp) Select[i].insert(*itSet);
proEmpty[i] = true;
}
if (j == pro[i].flag.size())
{
FollowIt(ltmp) Select[i].insert(*itSet);
proEmpty[i] = true;
}
Select[i].erase(terNum - 2);
}
cout << "各个产生式的Select集为: " << endl;
for (i = 0; i < proSize; ++i)
{
cout << "Select( " << nontInx[pro[i].leftPart] << "->";
for (j = 0; j < pro[i].flag.size(); ++j)
if (pro[i].flag[j])
cout << nontInx[pro[i].rightPart[j]];
else
cout << terInx[pro[i].rightPart[j]];
cout << ") = { ";
SelectIt(i) cout << terInx[*itSet] << " ";
cout << "}\n";
}
}
bool judegLL1()
{
for (int i = 0; i < nontNum; ++i)
{
for (int j = 0; j < nontPro[i].size() - 1; ++j)
{
for (int t = j + 1; t < nontPro[i].size(); ++t)
{
if (proEmpty[j] && proEmpty[t])
continue; //两个产生式都能产生空
for (itSet = Select[nontPro[i][j]].begin(); itSet != Select[nontPro[i][j]].end(); ++itSet)
{
if (Select[nontPro[i][t]].find(*itSet) != Select[nontPro[i][t]].end())
{
cout << terInx[*itSet] << "是产生式" << nontPro[i][j] << "和" << nontPro[i][t] << "的Select集合的交集,不是LL1文法\n";
return false;
}
}
}
}
}
return true;
}
void getAnalyzeTable()
{
analyzeTable = new vector<int>[nontNum]; //初始化-1,nontNum-1 表示#
for (int i = 0; i < nontNum; ++i)
analyzeTable[i].insert(analyzeTable[i].begin(), terNum, -1);
for (int i = 0; i < proSize; ++i)
{
SelectIt(i) analyzeTable[pro[i].leftPart][*itSet] = i;
}
cout << "该文法的预测分析表为:\n";
out(10, " ");
string outStr;
for (int i = 0; i < terNum; ++i)
out(10, terInx[i]);
cout << endl;
for (int i = 0; i < nontNum; ++i)
{
out(10, nontInx[i]);
for (int j = 0; j < terNum; ++j)
if (analyzeTable[i][j] == -1)
out(10, " ");
else
{
outStr = "->";
for (int t = analyzeTable[i][j], c = 0; c < pro[t].flag.size(); ++c)
if (pro[t].flag[c])
outStr += nontInx[pro[t].rightPart[c]];
else
outStr += terInx[pro[t].rightPart[c]];
out(10, outStr);
}
cout << endl;
}
}
void analysis()
{
int i = 0, ip = 0, outW = 30;
Sign X;
string outS = "";
out(10, "步骤");
out(outW, "分析栈");
out(outW, "剩余输入串");
out(outW, "所用产生式");
cout << endl;
analysisStack.clear();
analysisStack.push_back(Sign(terNum - 1, false));
analysisStack.push_back(Sign(nonter[start], true)); //对分析栈进行初始化
while (++i)
{
X = analysisStack.back();
analysisStack.pop_back();
if (X.flag == false && X.Inx == terNum - 1)
{
if (terInx[X.Inx] == language[ip])
{
out(10, i);
out(outW, terInx[terNum - 1]);
out(outW, terInx[terNum - 1]);
out(outW, "接受");
cout << "\n";
return;
}
else
{
cout << "你输入的语言该文法无法识别\n";
return;
}
}
else if (X.flag == false)
{
if (terInx[X.Inx] == language[ip])
{
outS = "";
for (int t = 0; t < analysisStack.size(); ++t)
if (analysisStack[t].flag)
outS += nontInx[analysisStack[t].Inx];
else
terInx[analysisStack[t].Inx];
outS += terInx[X.Inx];
out(10, i);
out(outW, outS);
outS = "";
for (int t = ip; t < language.size(); ++t)
outS += language[t];
out(outW, outS);
outS = "";
outS += language[ip];
out(outW, outS + "匹配");
cout << endl;
++ip;
}
else
{
cout << "你输入的语言该文法无法识别\n";
return;
}
}
else
{
int pos = analyzeTable[X.Inx][ter[language[ip]]];
if (pos == -1)
{
cout << "你输入的语言该文法无法识别\n";
return;
}
outS = "";
for (int t = 0; t < analysisStack.size(); ++t)
if (analysisStack[t].flag)
outS += nontInx[analysisStack[t].Inx];
else
terInx[analysisStack[t].Inx];
outS += terInx[X.Inx];
out(10, i);
out(outW, outS);
outS = "";
for (int t = ip; t < language.size(); ++t)
outS += language[t];
out(outW, outS);
outS = "";
outS += nontInx[X.Inx];
outS += "->";
for (int t = 0; t < pro[pos].flag.size(); ++t)
if (pro[pos].flag[t])
outS += nontInx[pro[pos].rightPart[t]];
else
outS += terInx[pro[pos].rightPart[t]];
out(outW, outS);
cout << endl;
if (pro[pos].flag[0] == false && proEmpty[pos])
continue;
for (int t = pro[pos].flag.size() - 1; t >= 0; --t)
if (pro[pos].flag[t])
analysisStack.push_back(Sign(pro[pos].rightPart[t], true));
else
analysisStack.push_back(Sign(pro[pos].rightPart[t], false));
}
}
}
测试
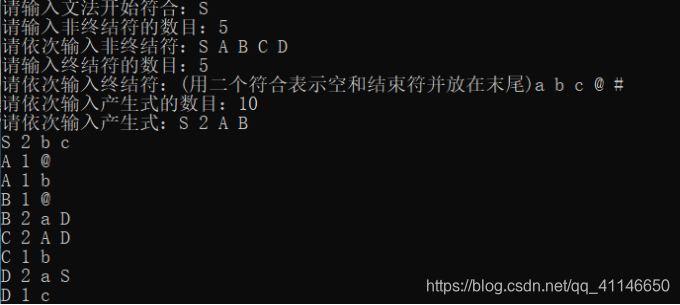
输入数据
S
5 S A B C D
5 a b c @ #
10
S 2 A B
S 2 b C
A 1 @
A 1 b
B 1 @
B 2 a D
C 2 A D
C 1 b
D 2 a S
D 1 c
截屏
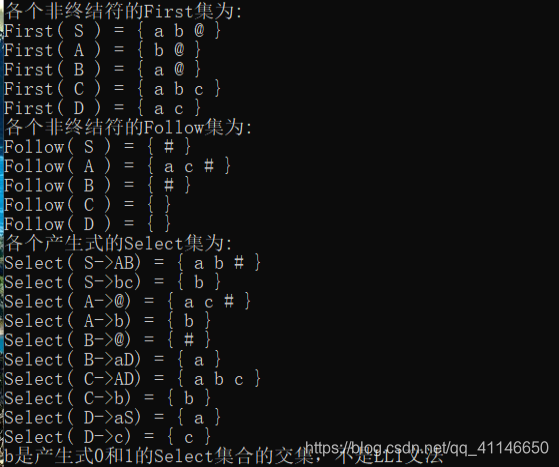








 本文介绍如何使用C++实现LL1文法的分析,包括计算First、Follow和Select集合,判断文法是否为LL1文法,构造预测分析表,并对输入字符串进行语法分析。
本文介绍如何使用C++实现LL1文法的分析,包括计算First、Follow和Select集合,判断文法是否为LL1文法,构造预测分析表,并对输入字符串进行语法分析。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








