2.1线性表的基本概念与实现

1、定义
具有相同特性元素的一个有限序列。该序列中所含元素个数是线性表的长度，用n表示，当n=0时，线性表为空。

2、逻辑特性
线性表只有一个表头元素，只有一个表尾元素，表头元素没有前驱，表尾元素没有后继，除表头和表尾元素之外，其他元素只有一个直接前驱，也只有一个直接后继。

3、线性表的存储结构
线性表的存储结构分为两种：顺序存储结构和链式存储结构。
（1）顺序表
线性表中所有元素按照其逻辑顺序，依次存储到从指定存储位置开始的一块连续的存储空间中。（第一个元素存储位置就是指定的存储位置,第i+1个元素紧接在第i个元素的存储位置后面）
（2）链表
每个结点包含所存元素信息和元素之间逻辑关系的信息，如单链表中前驱结点包含后继结点的地址信息。
（3）两种存储结构的比较
顺序表如图a
顺序表的第一个特性——随机访问特性（只要知道0点的位置，然后通过房间号就可以马上找出任何一个房间的为位置）
顺序表的第二个特性——要求占用连续的存储空间（存储分配只能预先进行，一旦分配好了，在对其操作过程中始终不变）
顺序表在插入的时候要移动多个元素

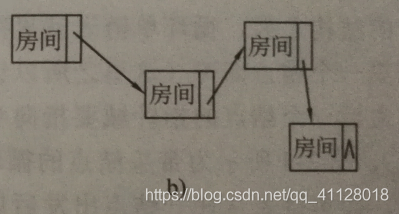
链表如图b
链表不支持随机访问（如果想访问最后一个房间，必须从第一个房间开始，依次走过前3个房间才能来到最后一个房间，不能直接找出最后一个房间）
链表中每一个结点用一部分空间来存储只想下一个结点位置的指针，因此链表中结点存储空间利用率较顺序表稍低一些
链表中当前结点的位置是由其前驱结点中的地址信息所指示的，而不是由其相对于初始位置的偏移量来确定。因此链表的结点可以散落在内存中的任意位置，且不需要一次性地划分所有结点所需的空间给链表，需要几个划几个。由此可见，链表支持存储空间的动态分配。
链表中进行插入操作无须移动元素

链表有一下5种形式

1）单链表。
在每个节点中除了包含数据域外，还包含一个指针域，用以指向后继节点。

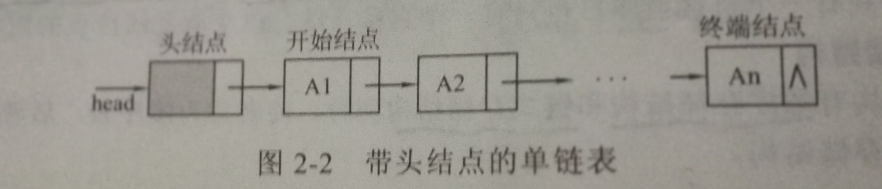
①带头结点的单链表中，头指针head指向头结点，头结点的值域不含任何信息，从头结点开始存储数据信息。头指针head始终不等于NULL，head->next等于NULL时，链表为空。
②不带头结点的单链表中的头指针head直接指向开始结点，即上图中的结点A1，当head等于NULL时，链表为空。
区别：带头结点的单链表有一个结点不存储信息，不带头结点的单链表的所有结点都存储信息。
Ps:在题目中要区分头结点和头指针，不论是带头节点的链表还是不带头结点的链表，头指针都指向链表中国第一个节点（即上图中的head指针）而头结点是带头结点链表中的第一个节点，只作为链表存在的标志。

2）双链表
双链表就是在单链表结点上增添了一个指针域，指向当前结点的前驱。（方便由后继找到前驱）

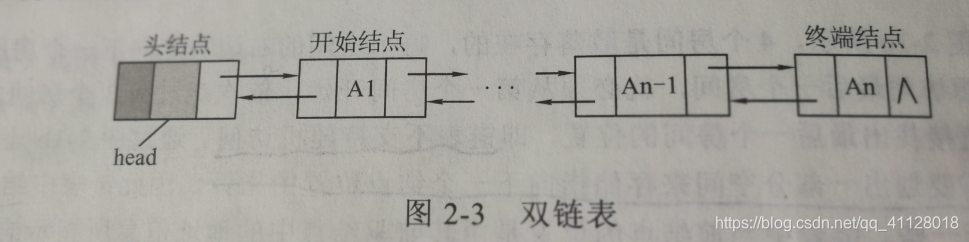
同样双链表也分为带头结点的双链表和不带头结点的双链表，情况类似于单链表。

3）循环单链表
将单链表的最后一个指针域（空指针）指向链表中的第一个结点即可(这里之所以说第一个结点而不说是头结点是因为：如果循环单链表是带头结点的，则最后一个结点的指针域要指向头结点；吐过循环链表不带头结点，则最后一个指针域要指向开始结点)。

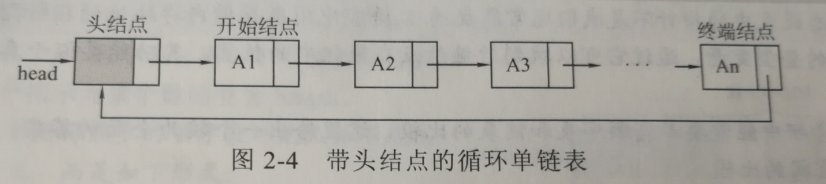
循环单链表可以实现从任何一个结点出发访问链表中的任何结点，而单链表从任一结点出发后只能访问这个结点本身及其后边的所有结点。（带头结点和不带头结点的情况与单链表相似）

4）循环双链表
将终端结点的next指针指向链表中的第一个结点，将链表中第一个结点的prior指针指向终端结点。循环双链表同样有带头结点和不带头结点之分。当head等于NULL时，不带头结点的循环双链表为空。带头结点的循环双链表中是没有空指针的。

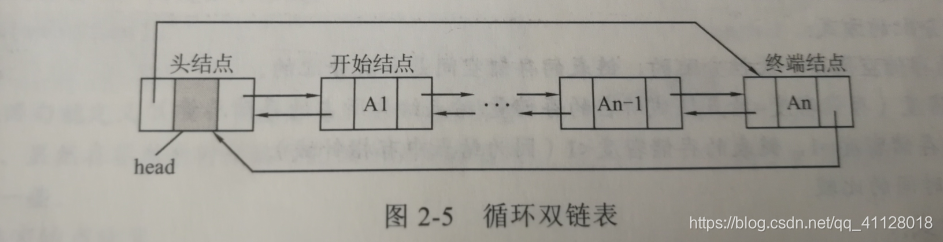
判断循环双链表为空（任意一句为真都可以判断）

head->next==head;
head->prior==head;
head->next==head&&head->prior==head;
head->next==head||head->prior==head;

上述4种链表如下图表示

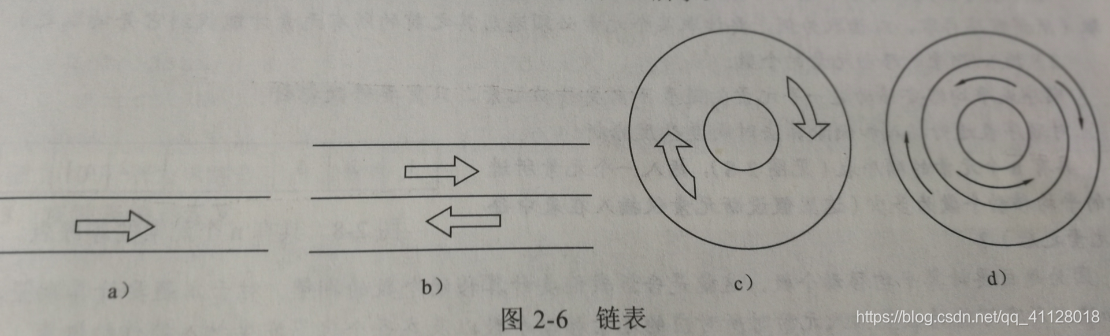
5）静态链表。
静态链表借助一维数组来表示，如图2-7所示。

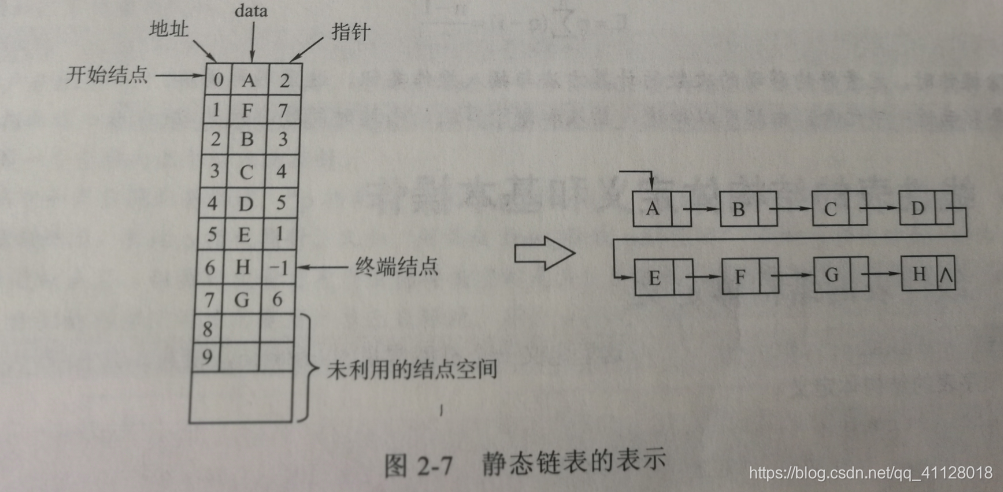
一般的链表结点空间来自于整个内存，静态链表则来自于一个结构体数组。数组中每一个结点有两个分量：一个是数据元素分量data；另一个是指针分量，指示了当前结点的直接后继结点在数组中的位置（这和一般链表中next指针的地位是等同的）

PS：静态链表中的指针不是我们通常所说的C语言中用来存储内存地址的指针型变量，而是一个存储数组下标的整型变量，通过它可以找到后继结点在数组中的位置，其功能类似于真实的指针，因此称其为指针。

说明：在考研中经常会考到顺序表和链表的比较，这里给出一个较为全面的答案。
（1）基于空间的比较
1）存储分配的方式：
顺序表的存储空间是一次性分配的，链表的存储空间是多次分配的。
2）存储密度（存储密度=结点值域所占的存储量/结点结构所占的存储总量）
顺序表的存储密度=1，链表的存储密度<1(因为结点中有指针域)。
（2）基于时间的比较
1）存取方式：
顺序表可以随机存取，亦可以顺序存取（对于顺序表，一般只答随机存取即可）；链表只能顺序存取（所谓顺序存取，以读取为例，要读取摸个元素必须遍历之前的所有元素才能找到它并读取之）。
2）插入/删除时移动元素的个数：
顺序表平均需要移动进一半元素；链表不需要移动元素，只需要修改指针。
对顺序表进行插入和删除算法时间复杂度分析:

具有n个元素的顺序表（见图2-8），插入一个元素所进行的平均移动个数为多少？（这里假设新元素仅插入在表中每个元素之后）？
因为题目要计算平均移动个数，这就是告诉我们要计算移动个数的期望。对于本题型要计算期望，就要知道在所有可能的位置插入元素时所对应的元素移动个数以及在每个位置发生插入操作的概率。
①求概率
因为插入位置的选择是随机的，所以所有位置被插入的可能性都是相同的，有n个可插入位置，所以任何一个位置被插入元素的概率都为p=1/n。
②求对应于每个插入位置需要移动的元素个数。
假设要把新元素插在表中第i个元素之后，则需要将第i个元素之后的所有元素往后移动一个位置，因此移动元素个数为n-i。
有①和②可知，移动元素个数的期望E为
E=p∑(n-i)=(n-1)/2 (i=1到i=n)
删除操作是，元素平均移动的次数的计算方法与插入操作类似。
即要移动近一半的元素，由此可知，插入和删除算法的平均时间复杂度为O(n)**