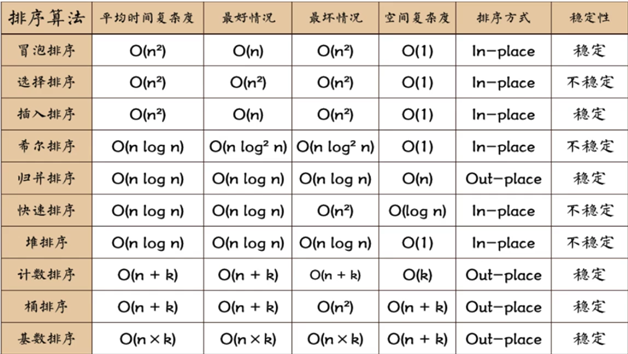
常用排序算法python实现_funssort ssort-优快云博客

排序算法属于计算机科学中的基础算法同时又应用非常广泛。python函数也内置了一些排序接口，如sorted函数。在实际生产里，不同场景我们使用的排序算法会稍有不同，排序算法选择主要考虑如下因素：

算法的执行效率
排序的稳定性
排序元素的个数
递归调用的开销

排序算法图解：

接下来介绍常用九大排序算法及python实现。

冒泡排序

基本思想：从左向右，两两比较，如果左边元素大于右边，就交换两个元素的位置。其中，每一轮排序，序列中最大的元素浮动到最右面。也就是说，每一轮排序，至少确保有一个元素在正确的位置。这样接下来的循环，就不需要考虑已经排好序的元素了，每次内层循环次数都会减一。

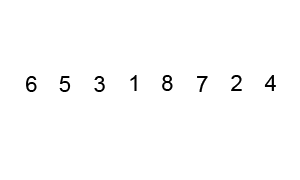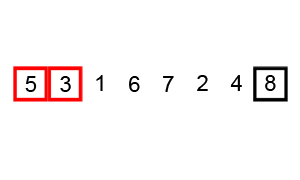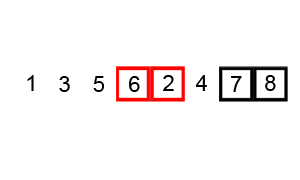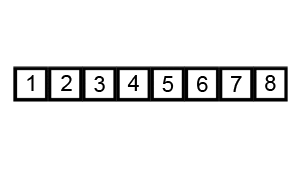
python实现：

def bubble_sort(a):    
  n, swap_size = len(a), 1    
  while swap_size > 0:        
        swap_size = 0        
        for i in range(n-1):            
            if a[i] > a[i+1]:                
               a[i],a[i+1] = a[i+1],a[i]               
               swap_size += 1        
         n-=1    
   return a

快速排序

基本思想：对冒泡排序的一种改进。通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小。然后再按此方法对这其中一部分数据进行快速排序，这是递归调用。再按此方法对另一部分数据进行快速排序，这也是递归调用。

快速排序评价：最坏时间复杂度为 O(n^2)，这是一种退化的情况，在大多数情况下只要选取了合适的划分元后，时间复杂度为 nlog(n)，快速排序通常比其他 O(nlogn) 算法更快，属于速度很快的非稳定排序算法。

python实现：


def quick_sort(a, left=None, right=None):
    left = 0 if not isinstance(left,(int, float)) else left
    right = len(a)-1 if not isinstance(right,(int, float)) else right
    if left < right:
        part_index = part(a, left, right)
        quick_sort(a, left, part_index-1)
        quick_sort(a, part_index+1, right)
    return a

def part(a, left, right):
    pivot = left
    index = pivot+1
    i = index
    while  i <= right:
        if a[i] < a[pivot]:
            a[i],a[index] = a[index],a[i]
            index+=1
        i+=1
    a[pivot],a[index-1] = a[index-1],a[pivot]
    return index-1

简单插入排序

基本思想：每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序，直到无序表内所有元素插入为止。最坏时间复杂度为 O(n^2)，属于稳定排序算法，对于处理小批量数据时高效。

python实现：


def insertion_sort(a):
    for i in range(len(a)):
        pre_index = i-1
        current = a[i]
        while pre_index >= 0 and a[pre_index] > current:
            a[pre_index+1] = a[pre_index]
            pre_index-=1
        a[pre_index+1] = current
    return a

希尔排序

基本思想：先取一个正整数 d1，以 d1 间隔分组，先对每个分组内的元素使用插入排序操作，重复上述分组和直接插入排序操作；直至 di = 1，即所有记录放进一个组中排序为止。

python实现：

import math
def shell_sort(a):
    gl=1
    while (gl < len(a)/3):
        gl = gl*3+1
    while gl > 0:
        for i in range(gl,len(a)):
            temp = a[i]
            j = i-gl
            while j >=0 and a[j] > temp:
                a[j+gl]=a[j]
                j-=gl
            a[j+gl] = temp
        gl = math.floor(gl/3)
    return a

简单选择排序

基本思想：是一个直接从未排序序列选择最值到已排序序列的过程，每一趟从待排序的数据元素中选出最小（最大）的元素，顺序放在待排序的数列最前，直到全部待排序的数据元素全部排完。

python实现：


def selection_sort(a):
    for i in range(len(a) - 1):
        min_index = i
        for j in range(i + 1, len(a)):
            if a[j] < a[min_index]:
                min_index = j
        if i != min_index:
            a[i], a[min_index] = a[min_index], a[i]
    return a

堆排序

基本思想：利用二叉树（堆）数据结构设计的一种排序算法，是对直接选择排序的一种改进算法。在逻辑结构上是按照二叉树存储结构，正是这种结构优化了选择排序的性能。在物理存储上是连续的数组存储，它利用了数组的特点快速定位指定索引的元素。

python实现：

import math

def heap_sort(a):
    al = len(a)

    def heapify(a, i):
        left = 2 * i + 1
        right = 2 * i + 2
        largest = i
        if left < al and a[left] > a[largest]:
            largest = left
        if right < al and a[right] > a[largest]:
            largest = right

        if largest != i:
            a[i], a[largest] = a[largest], a[i]
            heapify(a, largest)

    # 建堆
    for i in range(math.floor(len(a) / 2), -1, -1):
        heapify(a, i)

    # 不断调整堆：根与最后一个元素
    for i in range(len(a) - 1, 0, -1):
        a[0], a[i] = a[i], a[0]
        al -= 1
        heapify(a, 0)
    return a

归并排序

基本思想：它是建立在归并操作上的一种有效的排序算法，该算法采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

python实现：

import math
def merge_sort(a):
    if(len(a)<2):
        return a
    middle = math.floor(len(a)/2)
    left, right = a[0:middle], a[middle:]
    return merge(merge_sort(left), merge_sort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0));
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0));
    while right:
        result.append(right.pop(0));
    return result

基数排序

基本思想：将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

python实现：

import math
def radix_sort(a):
    i = 0 # 记录当前正在排拿一位，最低位为1
    max_num = max(a)  # 最大值
    j = len(str(max_num))  # 记录最大值的位数
    while i < j:
        bucket_list =[[] for _ in range(10)] #初始化桶数组
        for x in a:
            bucket_list[int(x / (10**i)) % 10].append(x) # 找到位置放入桶数组
        a.clear()
        for x in bucket_list:   # 放回原序列
            for y in x:
                a.append(y)
        i += 1
    return a

桶排序

基本思想：为了节省空间和时间，我们需要指定要排序的数据中最小以及最大的数字的值。将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。

python实现：


def bucket_sort(a):
    all_list = [0 for i in range(100)]  # 设置为全0的数组
    last_list = []
    for v in a:
        all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
    for i,t_v in enumerate(all_list):
        if t_v != 0:
            for j in range(t_v):
                 last_list.append(i)
    return last_list

最后，依次调用以上方法：


sort_funs = [bubble_sort,quick_sort,insertion_sort,shell_sort,selection_sort,heap_sort,merge_sort,radix_sort,bucket_sort]
a = [10, 7, 11, 7, 18, 17, 9, 17, 0, 7, 3, 20, 20, 15]
for fun in sort_funs:
    a_sorted = fun(a)
    print(a_sorted)

输出结果都一致（非降序序列）：

[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]
[0, 3, 7, 7, 7, 9, 10, 11, 15, 17, 17, 18, 20, 20]

总结：