java实现Tree Traversals Again

题目

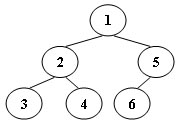
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

思路

这个题我的思路是:由入栈顺序得到树的先序遍历结果，由出栈顺序得到树的中序遍历结果，然后再推出树，进行后序遍历。看起来有点麻烦，有需要的可以参考一下。

代码

节点类

public class Node {
	private int data;
	private int left;
	private int right;
	
	public Node() {
		this.data = -1;
		this.left = -1;
		this.right = -1;
	}
	public Node(int a) {
		this.data = a;
		this.left = -1;
		this.right = -1;
	}
	public Node(int a, int left, int right) {
		this.data = a;
		this.left = left;
		this.right = right;
	}

	public int getData() {
		return data;
	}

	public void setData(int data) {
		this.data = data;
	}

	public int getLeft() {
		return left;
	}

	public void setLeft(int left) {
		this.left = left;
	}

	public int getRight() {
		return right;
	}

	public void setRight(int right) {
		this.right = right;
	}
}

测试类

public class Test {

	public static int flag=0;
	public static Node[] getTree(Scanner sc, int a) {
		Stack<Integer> stack = new Stack<>();//模拟出入栈操作
		Node[] n = new Node[a];
		Node[] preorder = new Node[a];	//先序遍历结果
		Node[] inorder = new Node[a];	//中序遍历结果
		for (int i = 0,j = 0, k = 0; i < 2*a; i++) {	//出入栈加起来一共有2a个
			String s = sc.next();	//接受输入数据
			Node node = new Node();
			if (s.equals("Push")) {	//push顺序相当于树先序遍历结果
				int num = sc.nextInt();
                stack.push(num);	//入栈，以便得到出栈的值
				node.setData(num);
				preorder[j] = node;
				j+=1;	
			}
			if (s.equals("Pop")) {	//pop顺序相当于树中序遍历结果
				int num = stack.pop();
				node.setData(num);
				inorder[k] = node;
				k+=1;
			}
		}
		n = toTree(preorder, 0, a-1, inorder, 0, a-1);//获取树
		return n;
	}
	//根据先序中序推出树
	public static Node[] toTree(Node[] n1, int start1, int end1,
			Node[] n2, int start2, int end2) {
		if(start1 > end1 || start2 > end2){//防止越界
			return null;
		}
		int root = n1[start1].getData();//获取根节点的值
		int rootIndex = findIndexInArray(n2, root);//获取中序遍历中根节点下标
		int value = rootIndex - start2;	//为左子树长度
		//构建左子树
		toTree(n1, start1+1, start1+value, n2, start2, rootIndex-1);
		//构建右子树
		toTree(n1, start1+value+1, end1, n2, rootIndex+1, end2);
		if (start1 < end1) {//防止越界
			n1[start1].setLeft(n1[start1+1].getData() - 1);
		}	//此时getData得到的是孩子节点的值：1，2，3，4，5，6，而他们对应的数组中的下标要-1
		if (start1+value < end1) {//防止越界
			n1[start1].setRight(n1[start1+value+1].getData()-1);
		}	//同上
		return n1;
	}
	//查找中序遍历的根节点下标
	private static int findIndexInArray(Node[] n, int rootData) {
		for (int i = 0; i < n.length; i++) {
			if(n[i].getData() == rootData){
				return i;
			}
		}
		return -1;
	}
	//后续遍历数组
	public static void postorder(Node[] n, int root) {	
		if (root != -1){
			postorder(n, n[root].getLeft());//添加左子树下标
			postorder(n, n[root].getRight());	//添加右子树下标
			if (flag == 0){//用来规范输出结果，保证末尾没有多余的空格
				System.out.print(n[root].getData());
				flag++;
			} else {
				System.out.print(" "+n[root].getData());
			}			
		}
	}
	
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int a = sc.nextInt();
		Node[] n = getTree(sc, a);
//		for (Node aaa: n) {	//打印出树
//			System.out.println(aaa.getData() +" "+aaa.getLeft()+" "+aaa.getRight());
//		}
		postorder(n, 0);	//调用方法后序遍历并输出
	}
}