吉首大学第八届“新星杯”大学生程序设计大赛 K: WaWa的难题（找规律）

最新推荐文章于 2020-12-28 11:47:28 发布

原创最新推荐文章于 2020-12-28 11:47:28 发布 · 378 阅读

CC 4.0 BY-SA版权

HaHa和WaWa面对期末复习期间遇到的一道排列组合难题，该题要求找出由1到N组成的特定排列数量，其中数字1始终位于首位，且任意两相邻数字之差不超过2。通过观察与尝试，最终发现了递推公式f[n]=f[n-1]+f[n-3]+1（n>3），用于高效求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【题目】

WaWa的难题

题目描述

HaHa和WaWa是好朋友，他们在临近期末的这段时间一起宅在图书馆学习。
今天HaHa在书上看到一个排列组合题目，思考很久后，仍然找不出其中的规律。
于是他把题目叙述给了WaWa。
题目：
————————————————————————
一个长度为N的排列，由数字1~N组成，它满足两个条件。
1、数字1永远在第一位。
2、任意两个相邻数字之差小于等于2。
现在给出一个N，
你能知道能组成多少个符合条件的排列吗？。
例如：
N=4
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
所以答案为4
————————————————————————
WaWa听后也是一脸懵逼。
现在WaWa想求助于你们，WaWa给出一个正整数N，问你用1~N能组成多少个符合题意的排列。

输入

多组数据。
每组数据输入一个正整数N(1<=N<=100)。

输出

输出符合题意的排列个数

样例输入 Copy

2
4

样例输出 Copy

1
4

【题解】

一开始以为是深搜，然后超时，试图优化无果，效率过低暴力跑到三十多就跑不动了。然后发现有规律。

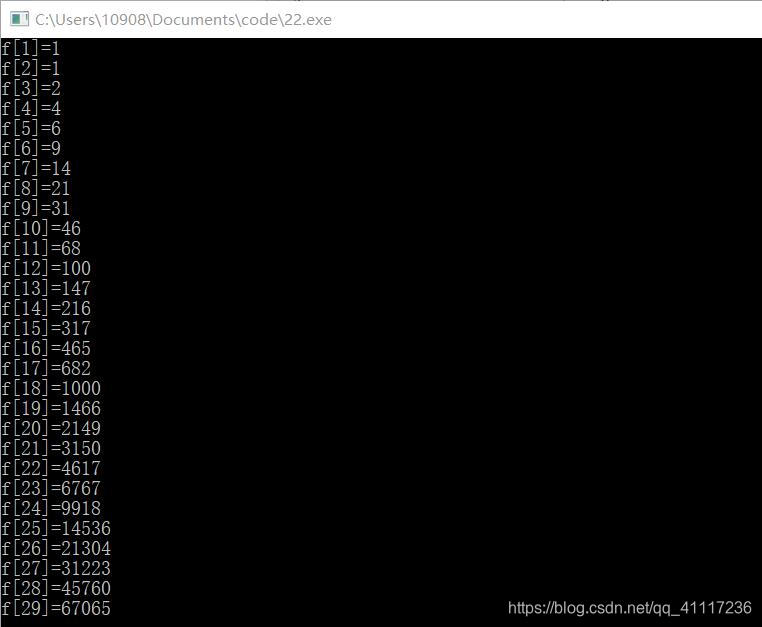
f[1]=1,f[2]=1,f[3]=2,f[n]=f[n-1]+f[n-3]+1(n>3)

【搜索代码】

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[105],vis[105]={0},ans;
void dfs(int pos,int n)
{
    if(pos==n)
    {
        ans++;
        return;
    }
    for(int i=2;i<=n;i++)
    {
        if(vis[i]==0&&abs(a[pos-1]-i)<=2)
        {
            a[pos]=i;
            vis[i]=1;
            dfs(pos+1,n);
            vis[i]=0;
        }
    }
}
int main()
{
    int n; a[0]=1;
    for(int n=1;n<=100;n++)
    {
        ans=0;
        dfs(1,n);
        printf("f[%d]=%d\n",ans);
    }
    return 0;
}

【代码】

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans[105];
void cul()
{
    ans[1]=1;ans[2]=1;ans[3]=2;
    for(int i=4;i<=100;i++)
        ans[i]=ans[i-1]+ans[i-3]+1;
}
int main()
{
    cul(); int n;
    while(~scanf("%d",&n))
        printf("%lld\n",ans[n]);
    return 0;
}