【Reasoning】Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine wi

Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B: A Technical Report

arxiv: https://arxiv.org/abs/2406.07394
github: https://github.com/trotsky1997/mathblackbox

问题背景

大模型在推理过程中存在幻觉问题，尽管Self-Refine可以通过重写技术进行一定的幻觉，但是仍然会存在错误问题。为了可以克服这个问题，作者提出了MCT Self-Refine（MCTSr）框架。通过将MCTS的系统探索能力与大型语言模型的Self-Refine和Self-Evaluation相结合，创建出了一个更鲁棒的的框架，以解决当前大型语言模型难以解决的复杂推理任务。在MCTS中，引入了一种动态修剪策略，该策略结合了改进UCB公式，以优化探索和挖掘之间的平衡。

本文方法

MCTSr的主要工作流如下：

• 初始化 ：根节点是使用基础模型生成的答案和虚拟响应（例如，“我不知道”）来建立的，以最小化模型过拟合倾向。

• 选择：算法采用价值函数Q对所有未完全被扩展的答案进行排序，并采用贪心策略选择值最高的节点进行进一步的探索和细化。

• 自精炼：选择的答案a使用自精炼框架进行优化。最初，模型生成一个关于a的反馈m，指导精炼过程产生一个改善的答案a '。

• 自我评价：通过一个评估模型对精炼后的答案进行从-100~100的评分以获得一个奖励值，并计算其Q值。作者在实践中发现，当没有特定约束的情况下，模型所输出的奖励值趋向于平滑。因此设计了三个约束：

  • prompt约束：模型在进行奖励评分时必须遵循最严格的标准。
  • 满分抑制：要求模型不提供完整的反馈分数；任何高于95分的奖励值都会被一个常量来抑制，降低其分数减少高分。
  • 重复采样：每次访问一个搜索树节点，都会对该节点的奖励进行重复采样，以增强自我评估的可靠性。需要注意的是，在对节点的子节点进行奖励采样的同时，还会对其父节点进行奖励采样，以增加奖励采样的样本量。采样后，计算a的Q值。为了抵消自奖励函数的平滑倾向，在期望奖励中加入最小值约束，进一步细化对答案质量的估计。
    
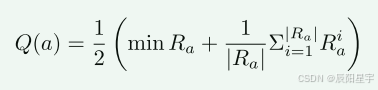
    Q(a)为答案a的质量值，Ra为a的奖励样本集合，minRa为Ra中的最小奖励，|Ra|为样本数量，∑i=1∣Ra∣Rai\sum_{i=1}^{|R_a|} R_a^i