(数据结构)栈和队列( C实现 )

栈和队列

• 1.栈

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

 说明 : 这里的栈是我们自己建立的一种自定义的数据结构 , 并非内存区域中的栈区, 当然他们也有共同的特点, 就是先进后出

内存中的栈区详解请点击跳转

• 先进后出

图解 : 

• 栈的实现

栈的实现可以用顺序表(数组)或链表来实现 , 相对而言顺序表(数组)的结构实现更优一些。因为顺序表(数组)在尾上插入数据的代价较小

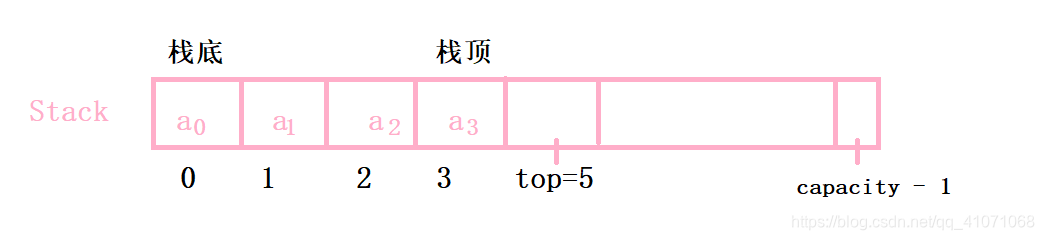 下面是定长的静态栈的结构，实际中一般不实用，所以我们主要实现下面的支持动态增长的栈

typedef int STDataType;
#define N 10
typedef struct Stack
{
STDataType _a[N];
int _top; // 栈顶
}Stack;

支持动态增长的栈

// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack {
	STDataType* _a;
	int _top; // 栈顶
	int _capacity; // 容量
}Stack;

 在stack.h中声明

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define N 10
// 支持动态增长的栈
typedef int STDataType;
typedef struct Stack {
	STDataType* _a;
	int _top; // 栈顶
	int _capacity; // 容量
}Stack;
void StackInit(Stack* ps);
void StackDestory(Stack* ps);
void StackPush(Stack* ps, STDataType x);
void StackPop(Stack* ps);
STDataType StackTop(Stack* ps);
int StackEmpty(Stack* ps);
int StackSize(Stack* ps);
void StackPrint(Stack* ps);

在 stack.c中实现函数定义

#include"stack.h"

void StackInit(Stack* ps) {
	assert(ps);
	ps->_a = (STDataType*)calloc(N, sizeof(STDataType));
	ps->_capacity = N;
	ps->_top = 0;
}
void StackDestory(Stack* ps) {
	assert(ps);
	if (ps->_a) {
		ps->_top = 0;
		ps->_capacity = 0;
		free(ps->_a);
	}
}
void StackPush(Stack* ps, STDataType x) {
	assert(ps);
	if (ps->_top >= ps->_capacity) {
		ps->_capacity *= 2;
		ps->_a = (STDataType*)realloc(ps->_a, ps->_capacity * sizeof(STDataType));
	}
	ps->_a[ps->_top] = x;
	++ps->_top;
}
void StackPop(Stack* ps) {
	assert(ps);
	--ps->_top;
}
STDataType StackTop(Stack* ps) {
	assert(ps);
	return ps->_a[ps->_top - 1];
}
int StackEmpty(Stack* ps) {
	assert(ps);
	return ps->_top != 0;
}
int StackSize(Stack* ps) {
	assert(ps);
	return ps->_top;
}
void StackPrint(Stack* ps) {
	for (int i = 0; i < ps->_top; ++i) {
		printf("%d ", ps->_a[i]);
	}
	putchar('\n');
}

调试入口main.c

#include"stack.h"

int main() {
	Stack s;
	Stack* p = &s;
	StackInit(p);
	for (int i = 0; i < 20; ++i) {
		StackPush(p, i);
	}
	StackPrint(p);
	StackPush(p, 100);
	StackPrint(p);
	StackPop(p);
	StackPrint(p);
	system("pause");
	return 0;
}

 

---

 

• 2.队列

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数
组头上出数据，效率会比较低。

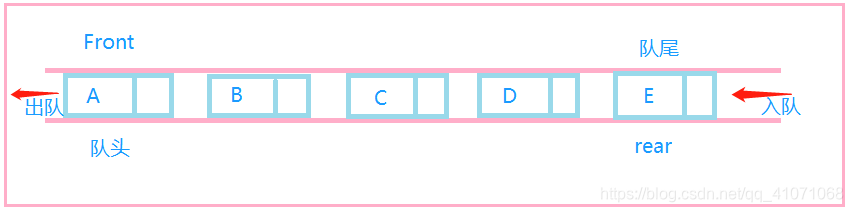
队列的实现

在queue.h中声明

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int QUDataType;
typedef struct QueueNode{
	struct QueueNode* _next;
	QUDataType _data;
}QueueNode;
typedef struct Queue{
	QueueNode* _front; // 队头
	QueueNode* _rear; // 队尾
}Queue;

void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
QueueNode* BuyQueueNode(QUDataType x);
void QueuePush(Queue* pq, QUDataType x);
void QueuePop(Queue* pq);
QUDataType QueueFront(Queue* pq);
QUDataType QueueBack(Queue* pq);
int QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);
void QueuePrint(Queue* pq);

 在queue.c中实现函数

#include"queue.h"
void QueueInit(Queue* pq) {
	assert(pq);
	pq->_front = NULL;
	pq->_rear = NULL;
}
void QueueDestory(Queue* pq) {
	assert(pq);
	QueueNode* tmp;
	while (pq->_front) {
		tmp = pq->_front;
		pq->_front = tmp->_next;
		free(tmp);
	}
}
void QueuePush(Queue* pq, QUDataType x) {
	assert(pq);
	QueueNode* cur = (QueueNode*)calloc(1, sizeof(QueueNode));
	cur->_data = x;
	if (pq->_front == NULL) {
		pq->_front = pq->_rear = cur;
	}
	cur->_next = NULL;
	pq->_rear->_next = cur;
	pq->_rear = cur;
}
void QueuePop(Queue* pq) {
	assert(pq);
	QueueNode* tmp;
	tmp = pq->_front;
	pq->_front = tmp->_next;
	free(tmp);
}
QUDataType QueueFront(Queue* pq) {
	assert(pq);
	return pq->_front->_data;
}
QUDataType QueueBack(Queue* pq) {
	assert(pq);
	return pq->_rear->_data;
}
int QueueEmpty(Queue* pq) {
	assert(pq);
	return pq->_front == NULL;
}
int QueueSize(Queue* pq) {
	assert(pq);
	QueueNode* cur = pq->_front;
	int count = 0;
	while (cur) {
		++count;
		if (cur == pq->_rear) {
			break;
		}
		cur = cur->_next;
	}
	return count;
}
void QueuePrint(Queue* pq) {
	assert(pq);
	for (QueueNode* cur = pq->_front; cur; cur = cur->_next) {
		printf("%d ", cur->_data);
		if (cur == pq->_rear) {
			break;
		}
	}
	putchar('\n');
}

 调试入口main.c

#include"queue.h"

int main() {

	Queue test;
	QueueInit(&test);
	for (int i = 1; i <= 10; ++i) {
		QueuePush(&test, i);
	}
	QueuePrint(&test);
	QueuePop(&test);
	QueuePrint(&test);
	printf("%d\n", QueueFront(&test));
	printf("%d\n", QueueBack(&test));
	printf("%d\n", QueueSize(&test));
	system("pause");
	return 0;
}

扩展 :

实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列可以使用数组(顺序表)实现，也可以使用循环链表实现。

这两种方法在以后再写

---