回溯法解01背包问题

概念：

  回溯法采用深搜+剪枝来搜索生成树：

步骤：

1.

假设规定左叉标1（代表选择该物品装入背包），右叉标0（代表不选择该物品装入背包）。给定示例输入：

背包容量c=10

物品个数n=5

物品重量w={2，2，6，5，4}

物品价格p={6，3，5，4，6}

注意：

    左子树的解的上界与父节点相同，不用计算。右子树的解的界值：较好的就算方法是将剩余物品依其单位重量价值排序，然后依次装入物品，直到装不下时，再装入该物品的一部分来装满背包。由此得到的价值是右子树中解的上界（尽管这不是一个可行解，但可以证明其价值是最优值的上界）。-----每次进入右子树之前都会计算右子树的界，如果右子树的界大于当前的界，则才能进入右子树（即右子树的界满足约束条件）。每走到一个叶结点时就更新当前的界。

预处理：将物品按照单位重量的价格排序如下：

              物品重量w={2，2，4，6，5}

              物品价格p={6，3，6，5，4}

   界的计算：

                2号结点的界：（3+6）+（10-2-4）*（5/6）=12.333；

                4号结点的界：6+6+（10-2-4）*（5/6）=15.33；

                8号结点的界：（6+3+5）+（10-2-2-6）*（4/5） = 14

                16号结点的界：（6+3+6）+（10-2-2-4）*（4/5）=16.6 （计算机处理float类型的16.6的表示形式是16.6000000004）               

生成树的表示：
 

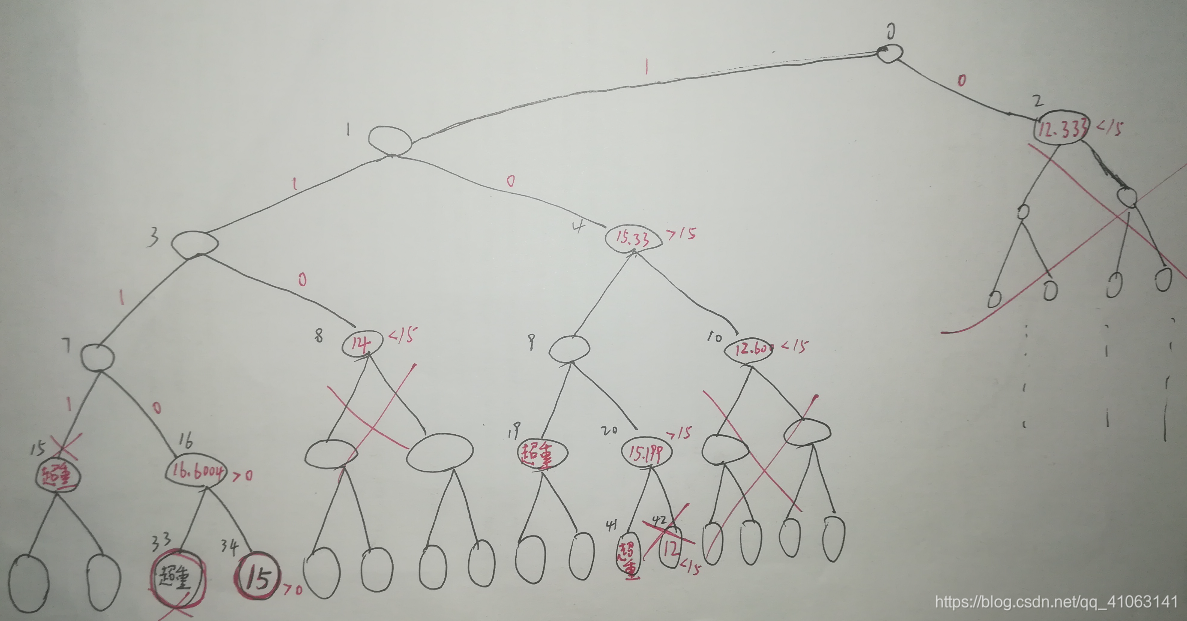
2.程序运行时。从0结点开始出发：只要遇到1就一直往左走（先逐个将物品装入背包，直到装不下再向右走），直到背包装不下物品，才想右走。

程序的路线图：0-1-3-7结点（选择1，2，3号物品装入背包），当要走15结点时，发现背包超重了，（即4号物品放弃装包） ，此时向右走到16结点。对16结点进行判定：16结点的界是16.6，大于当前界0（初始的界为0），所以可以向右走到16结点，然后遇到1，向左走到33结点，选择5号物品装包，又超重了，故向右有，5号不装包。34结点的界满足要求，可以向右走到34结点，此时已经走到了一个叶结点（34结点），所以将，更新当前界的值（初始时当前界的值设为0），此时当前界的值从0变到了15.

然后从34回溯到16-->7-->3,马上要进入8结点了，经计算，8结点的界为（6+3+5）+（10-2-2-6）*（4/5） = 14<15,故8结点不能走，再回溯到1，对4结点判定，可走。然后到9，再走19超重，那就向右走20，接着走41超重，走42，它的界为12<15不满足约束条件，故12结点不能走，因为还没走到叶结点，所以当前的界仍然是15，----回溯到4，走10不行，回溯到0，走2，不行。至此：回溯的递归调用结束。从生成树的遍历路径知道：最佳方案：应该选1，2，3号物品装包。

代码实现：

#include<iostream>
#include<algorithm>
using namespace std;


class Knap {
	friend int knapsack(int *,int *,int ,int);
private:
	float Bound(int i);
	void Backtrack(int i);
	int c;		//背包容量
	int n;		  //物品数
	int *w;     //物品重量数组
	int *p;		//物品价值数组
	int cw;		//当前重量
	int cp;		//当前价值
	int bestp;    //当前最优价值
};


void Knap::Backtrack(int i) {
	if (i > n) {
		//到达叶结点
		bestp = cp;
		return;
	}

	if (cw + w[i] <= c) { //进入左子树
		cw += w[i];
		cp += p[i];
		Backtrack(i + 1);
		cw -= w[i];
		cp -= p[i];
	}
//	float u=Bound(i + 1);
//	float bb=bestp;
	//当前的界是否大于背包当前的值
		if (Bound(i + 1) > bestp) { //进入右子树
			Backtrack(i + 1);
		}
}


float Knap::Bound(int i) {
	//计算上界
	int cleft = c - cw; //剩余容量
	float b = cp;
	//以物品单位重量价值递减序装入物品
	while (i <= n && w[i] <= cleft) {
		cleft -= w[i];
		b += p[i];
		i++;
	}
	//装满背包
	if (i <= n){
		float aa=p[i] * cleft;
		float bb=w[i];
		float temp=aa/bb;
//注意：如果这样写：float temp=p[i] * cleft/w[i];则temp计算出来是整数，因为右边是先按整数来算，再将int转float；
		b += temp;
		cout<<b<<endl;
	}
	return b;
};
class Object {
	friend int knapsack(int *,int *,int,int);
  public:
	int operator<=(Object a) const {
		return (d >= a.d);
	}
  private:
	int ID;
	float d;
};


int knapsack(int p[], int w[], int c, int n) {
	//为Knap: Backtrack初始化
	int W = 0;
	int P = 0;
	Object * Q = new Object[n];
	for (int i = 1; i <= n; i++) {
		Q[i - 1].ID = i;
		Q[i - 1].d = 1.0 * p[i]/w[i];
		//cout<<Q[i - 1].d<<endl;
		P += p[i];
		W += w[i];
	}
	if (W <= c) return P; //装入所有物品
	//所有物品的总重量大于背包容量c,存在最佳装包方案

		//sort(Q,n);对物品以单位重量价值降序排序（不排序也可以，但是为了便于计算上界，可将其按照单位重量价格从大到小排序）

		//1.对物品以单位重量价值降序排序

		//采用简单冒泡排序

		for(int i = 1; i<n; i++)

			for(int j = 1; j<= n-i; j++)

			{

				if(Q[j-1].d < Q[j].d)

				{

					Object temp = Q[j-1];

					Q[j-1] = Q[j];

					Q[j] = temp;

				}

			}

    Knap K;
	K.p = new int[n + 1];
	K.w = new int[n + 1];
	for (int i = 1; i <= n; i++) {
		K.p[i] = p[Q[i - 1].ID];
		K.w[i] = w[Q[i - 1].ID];
	}
	K.cp = 0;
	K.cw = 0;
	K.c = c;
	K.n = n;
	K.bestp = 0;
	//回溯搜索
	K.Backtrack(1);
	delete[] Q;
	delete[] K.w;
	delete[] K.p;
	return K.bestp;
}

int main(){
    int p[]={0,4,6,3,5,6};
    int w[]={0,5,4,2,6,2};
    //排好序之后的：
//    int p[]={0,6,3,6,5,4};
//    int w[]={0,2,2,4,6,5};
	int c=knapsack(p,w,10,5);
	cout<<"01背包问题的最有值为："<<c;
	return 0;
}